Timed Automata COURSE CS 60030 FORMAL SYSTEMS Pallab

Timed Automata COURSE: CS 60030 FORMAL SYSTEMS Pallab Dasgupta, Professor, Dept. of Computer Sc & Engg Antonio Bruto da Costa, Research Scholar, INDIAN INSTITUTE OF TECHNOLOGY 1 Dept. of Computer Sc & Engg

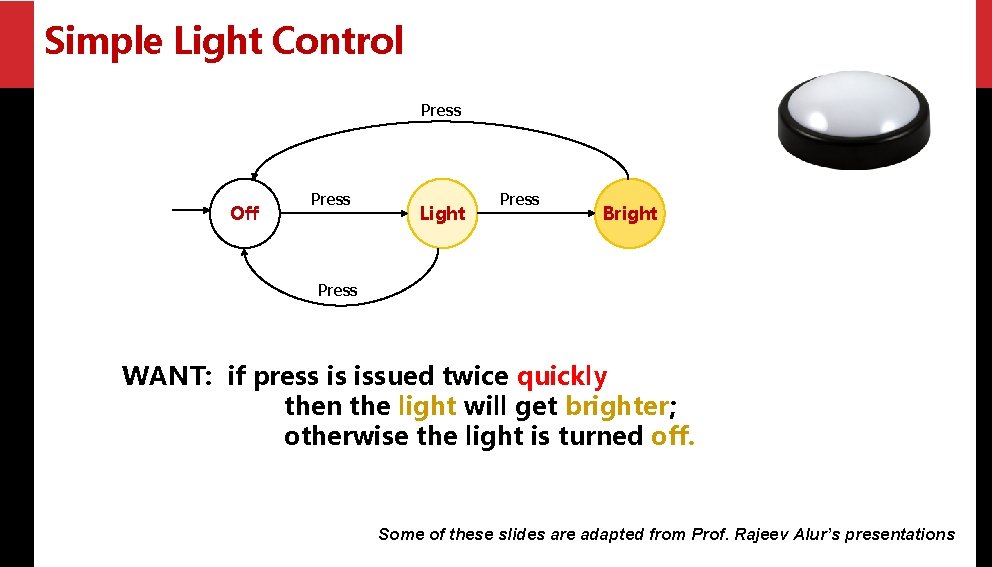
Simple Light Control Press Off Press Light Press Bright Press WANT: if press is issued twice quickly then the light will get brighter; otherwise the light is turned off. Some of these slides are adapted from Prof. Rajeev Alur’s presentations

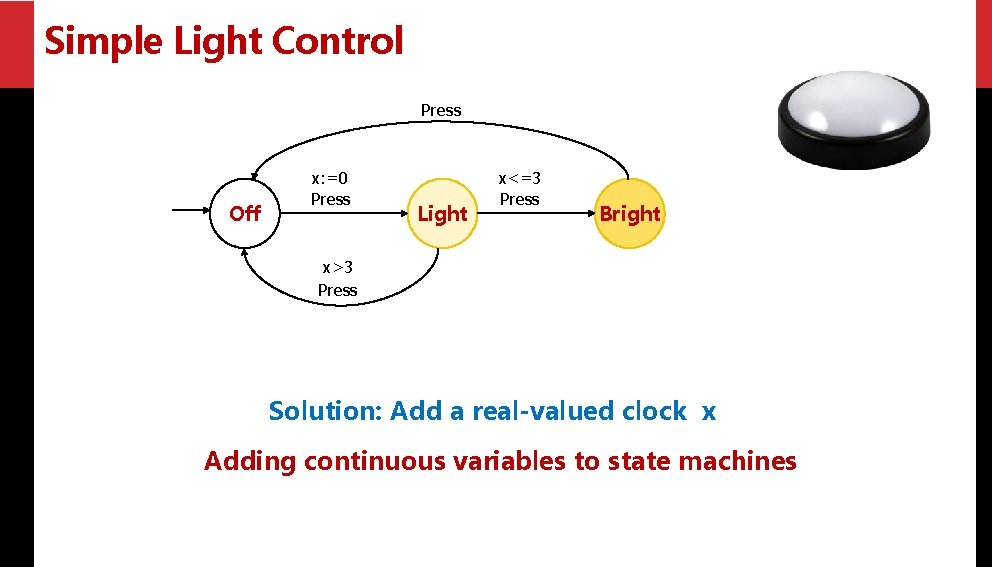
Simple Light Control Press Off x: =0 Press Light x<=3 Press Bright x>3 Press Solution: Add a real-valued clock x Adding continuous variables to state machines

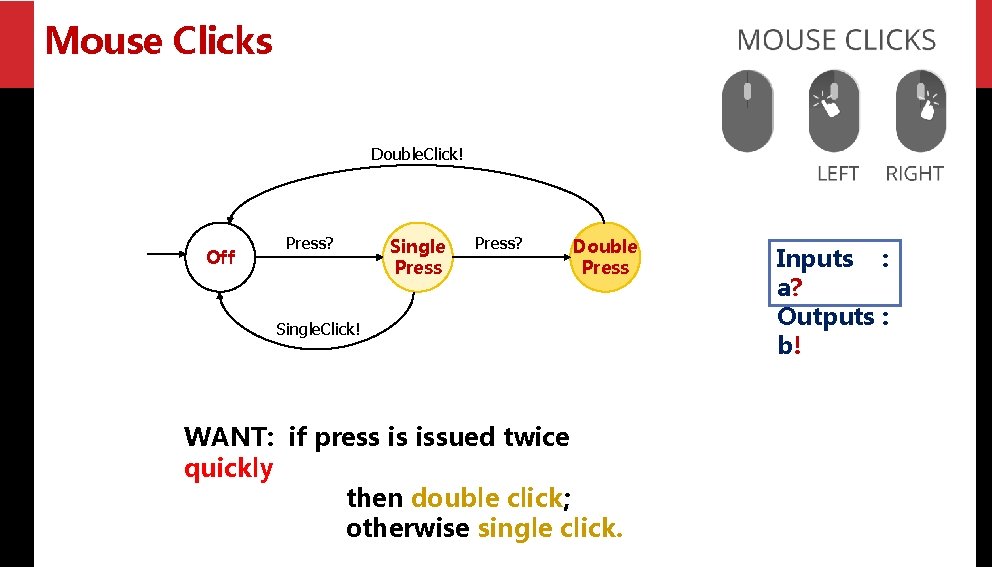
Mouse Clicks Double. Click! Off Press? Single Press? Double Press Single. Click! WANT: if press is issued twice quickly then double click; otherwise single click. Inputs : a? Outputs : b!

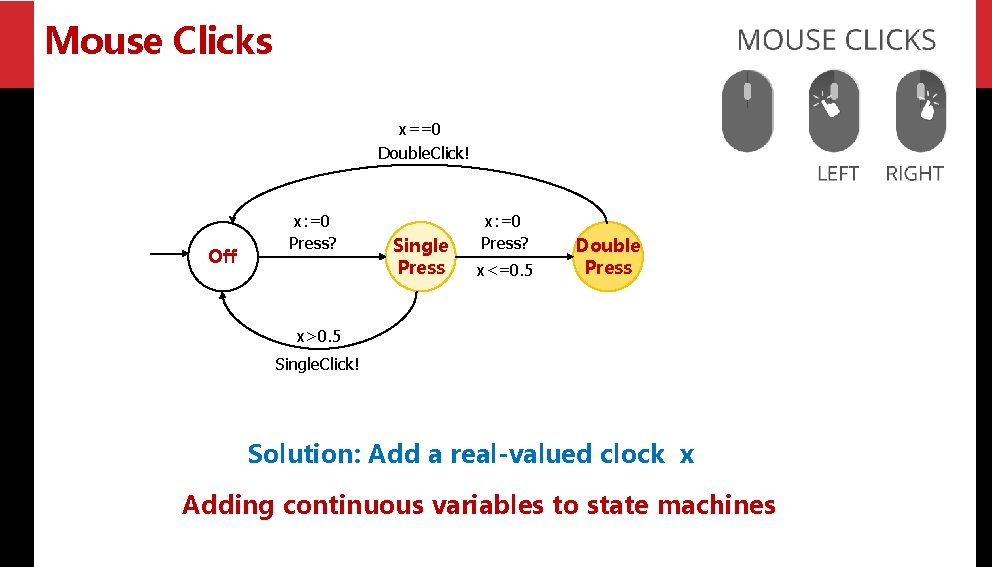
Mouse Clicks x==0 Double. Click! Off x: =0 Press? Single Press x: =0 Press? x<=0. 5 Double Press x>0. 5 Single. Click! Solution: Add a real-valued clock x Adding continuous variables to state machines

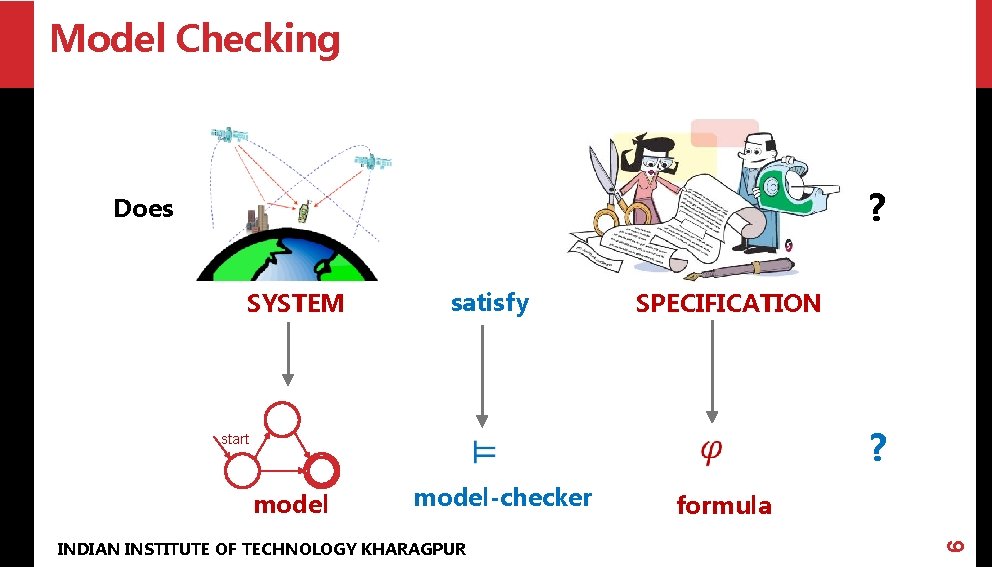
Model Checking ? Does satisfy start model-checker INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR SPECIFICATION ? formula 6 SYSTEM

Systems and Automata Systems under analysis are modeled and represented as transition systems: Finite automata Pushdown automata Program graphs Timed automata Hybrid automata Petri Nets Channel Systems Message Sequence Charts … INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 7 q q q q q

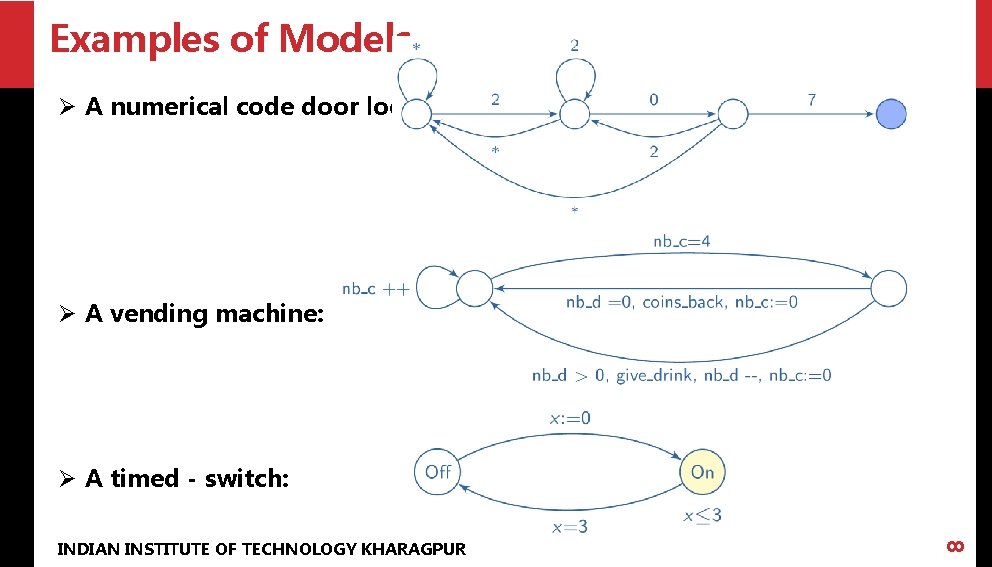
Examples of Models Ø A numerical code door lock: Ø A vending machine: INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 8 Ø A timed - switch:

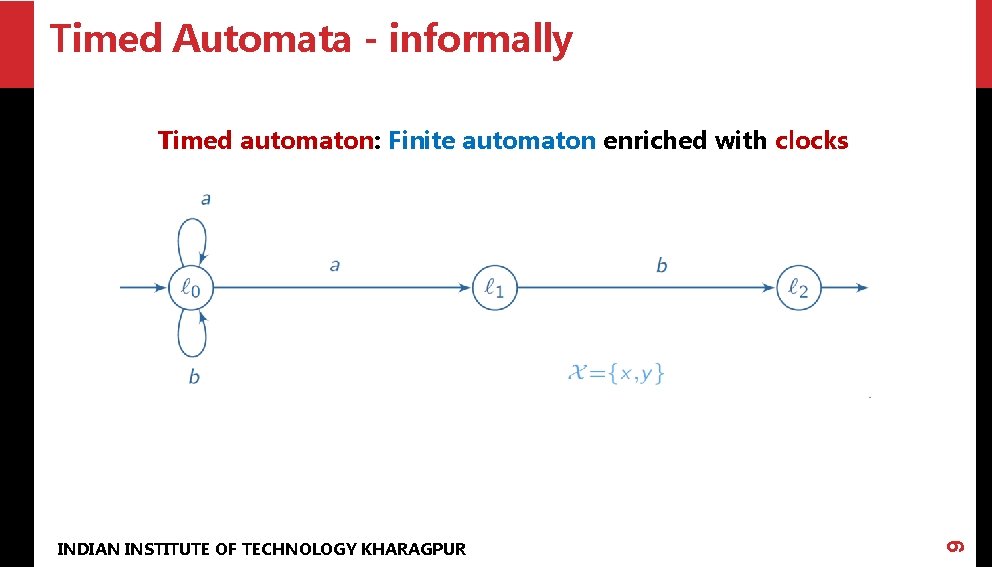
Timed Automata - informally INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 9 Timed automaton: Finite automaton enriched with clocks

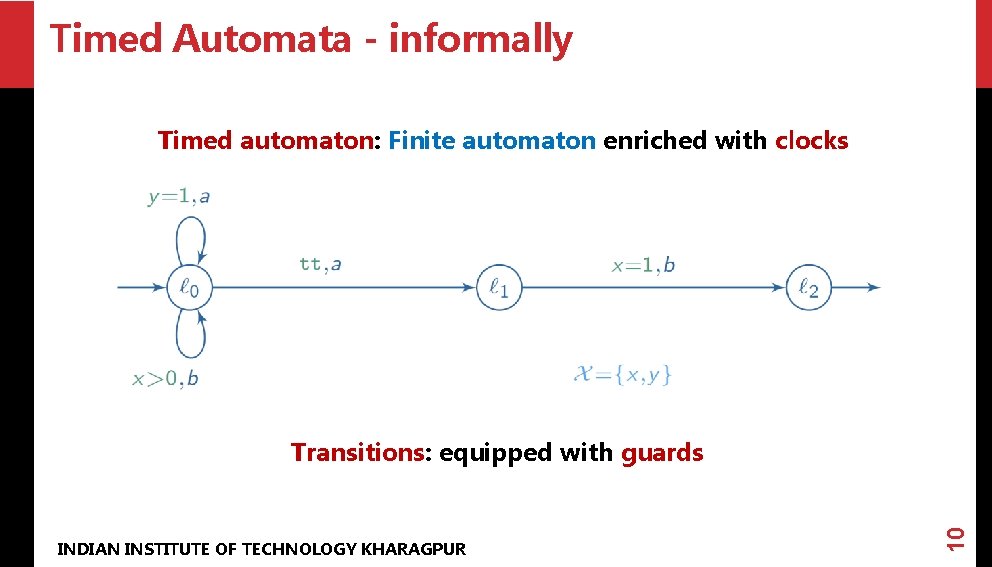
Timed Automata - informally Timed automaton: Finite automaton enriched with clocks INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 10 Transitions: equipped with guards

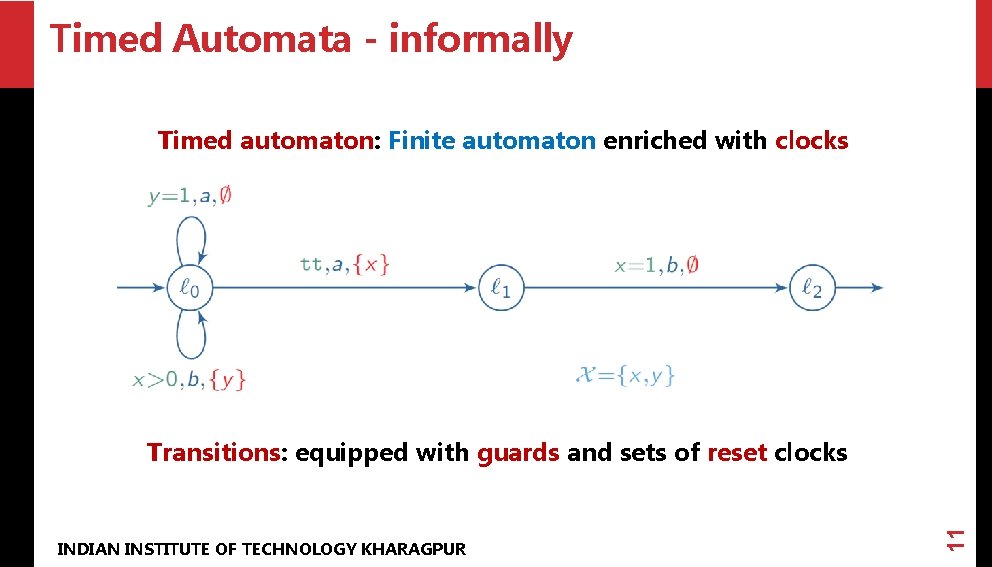
Timed Automata - informally Timed automaton: Finite automaton enriched with clocks INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 11 Transitions: equipped with guards and sets of reset clocks

Timed Automaton - Model Structure INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 12

Timed Automaton - Semantics INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 13

Runs, Sequences, Words, Languages Run of A : or simply INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 14

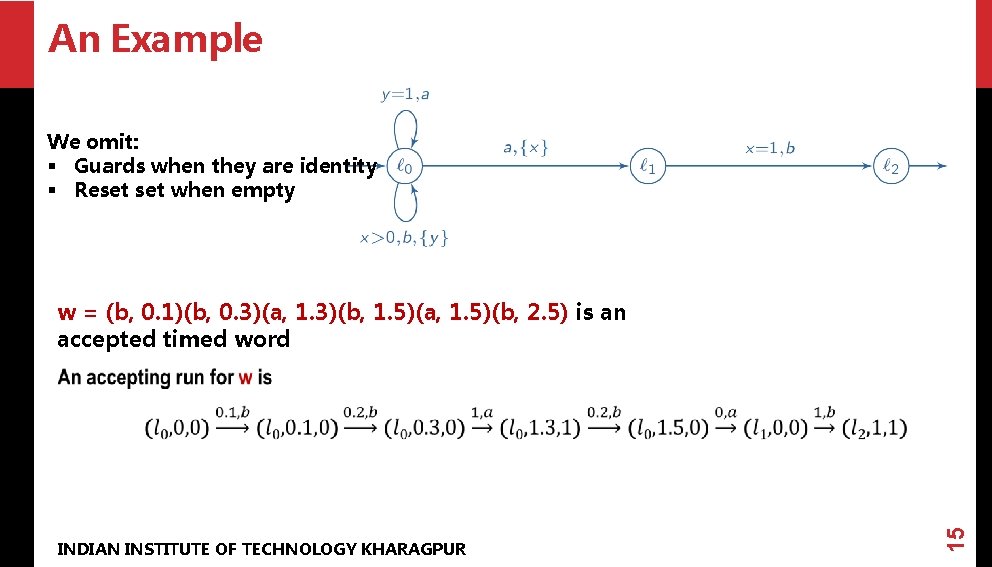
An Example We omit: § Guards when they are identity § Reset when empty w = (b, 0. 1)(b, 0. 3)(a, 1. 3)(b, 1. 5)(a, 1. 5)(b, 2. 5) is an accepted timed word INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 15

More Examples INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 16 Does there exist an accepted timed word containing action b?

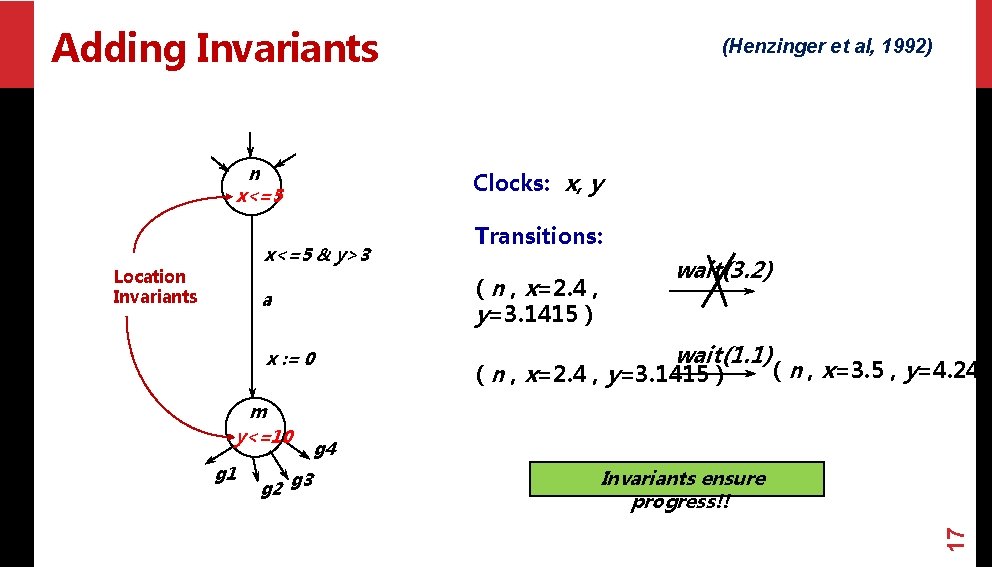
Adding Invariants n x<=5 Clocks: x, y x<=5 & y>3 x : = 0 g 1 g 2 g 3 wait(3. 2) ( n , x=2. 4 , y=3. 1415 ) a m y<=10 Transitions: wait(1. 1) ( n , x=2. 4 , y=3. 1415 ) ( n , x=3. 5 , y=4. 241 g 4 Invariants ensure progress!! 17 Location Invariants (Henzinger et al, 1992)

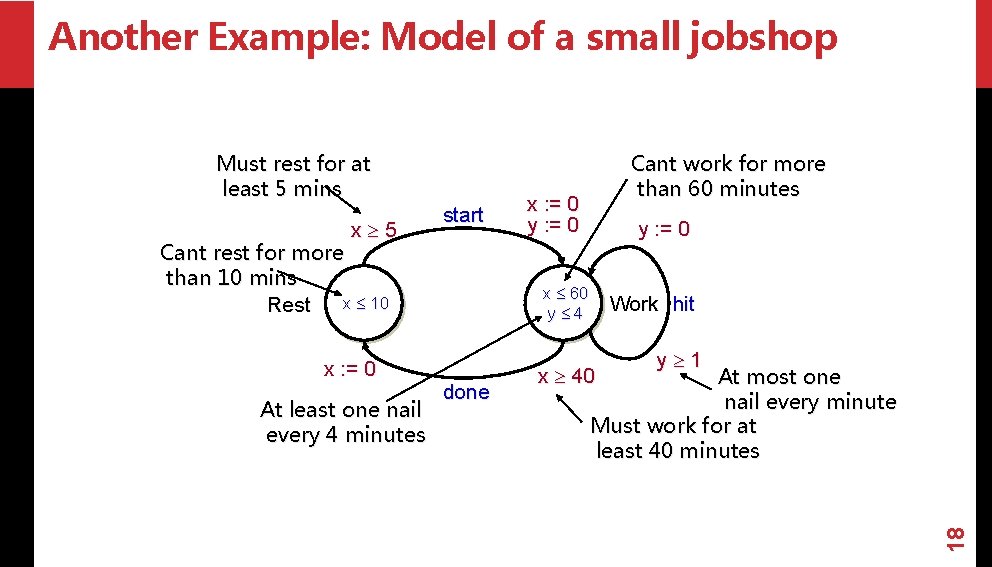
Another Example: Model of a small jobshop x 5 Cant rest for more than 10 mins Rest x 10 x : = 0 At least one nail every 4 minutes start Cant work for more than 60 minutes x : = 0 y : = 0 x 60 y 4 done Work hit y 1 At most one nail every minute Must work for at least 40 minutes x 40 18 Must rest for at least 5 mins

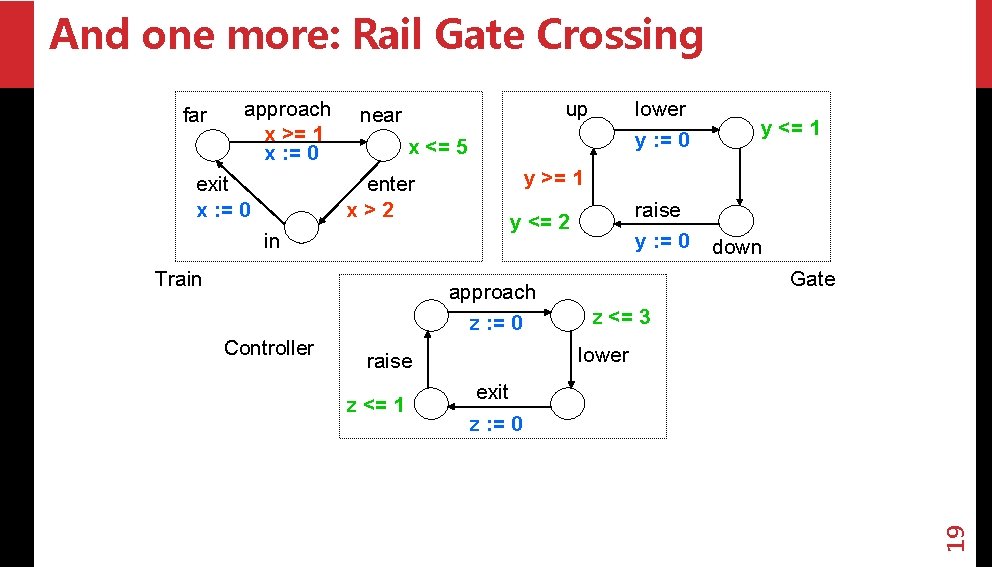
And one more: Rail Gate Crossing approach x >= 1 x : = 0 exit x : = 0 up near x <= 5 enter x>2 in Train raise y : = 0 y <= 2 down Gate z <= 3 lower raise z <= 1 y >= 1 approach z : = 0 Controller lower y : = 0 exit z : = 0 19 far

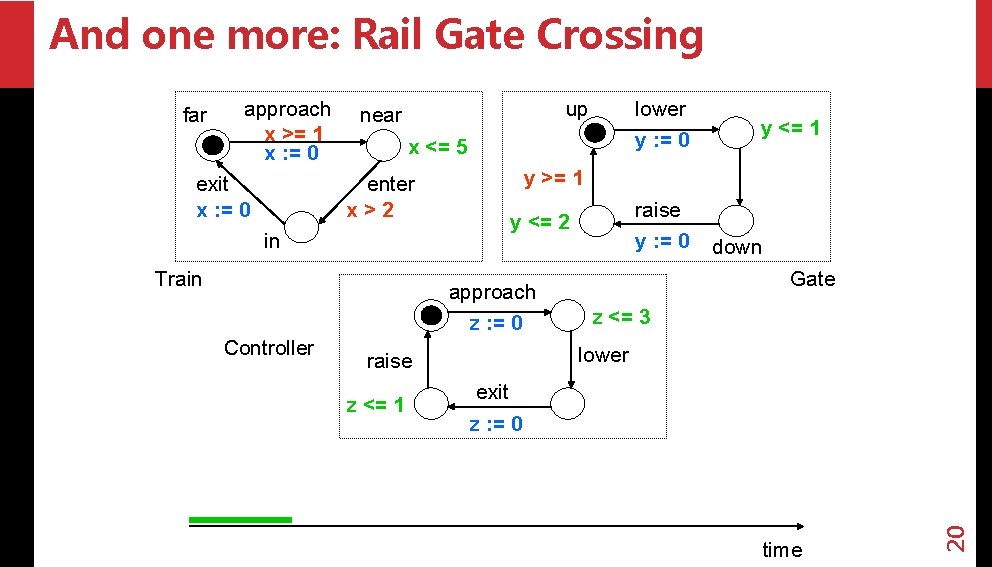
And one more: Rail Gate Crossing approach x >= 1 x : = 0 exit x : = 0 up near x <= 5 enter x>2 in Train raise y <= 2 y : = 0 down Gate z <= 3 lower raise z <= 1 y >= 1 approach z : = 0 Controller lower y : = 0 exit z : = 0 time 20 far

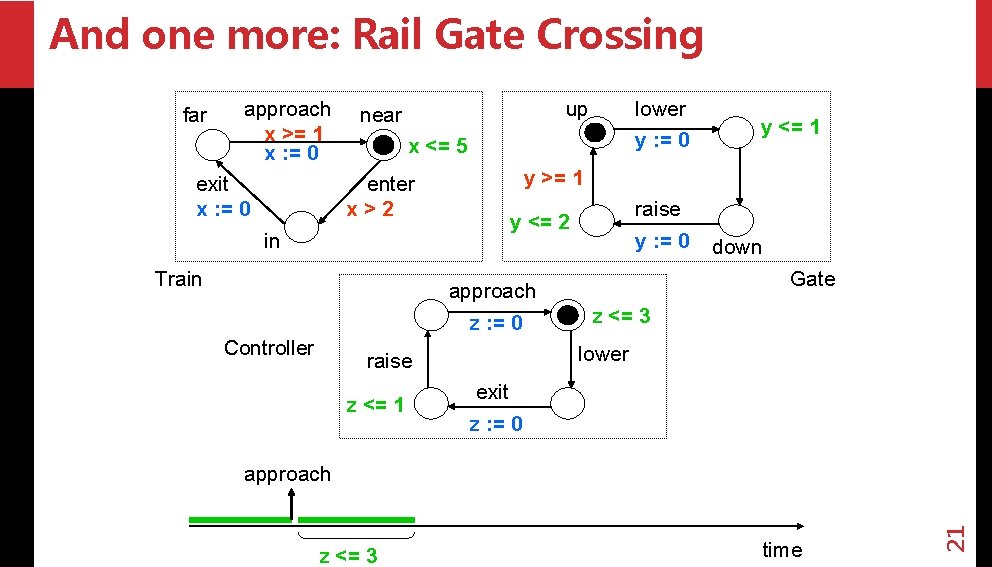
And one more: Rail Gate Crossing approach x >= 1 x : = 0 exit x : = 0 up near y : = 0 x <= 5 enter x>2 in Train raise y : = 0 y <= 2 down Gate z <= 3 lower raise z <= 1 y >= 1 approach z : = 0 Controller lower exit z : = 0 approach z <= 3 time 21 far

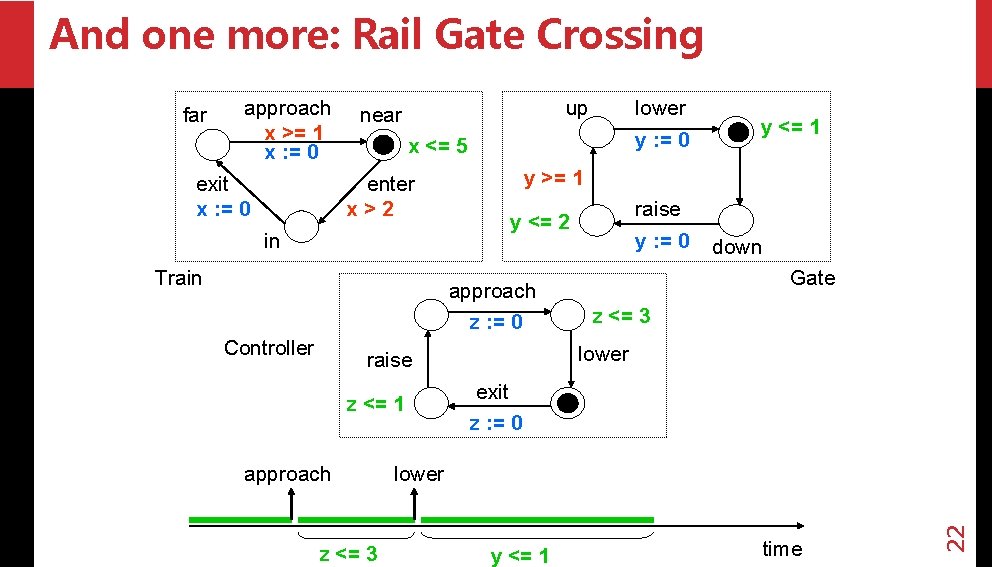
And one more: Rail Gate Crossing approach x >= 1 x : = 0 exit x : = 0 up near y : = 0 x <= 5 enter x>2 in Train approach z <= 3 raise y : = 0 y <= 2 down Gate z <= 3 lower raise z <= 1 y >= 1 approach z : = 0 Controller lower exit z : = 0 lower y <= 1 time 22 far

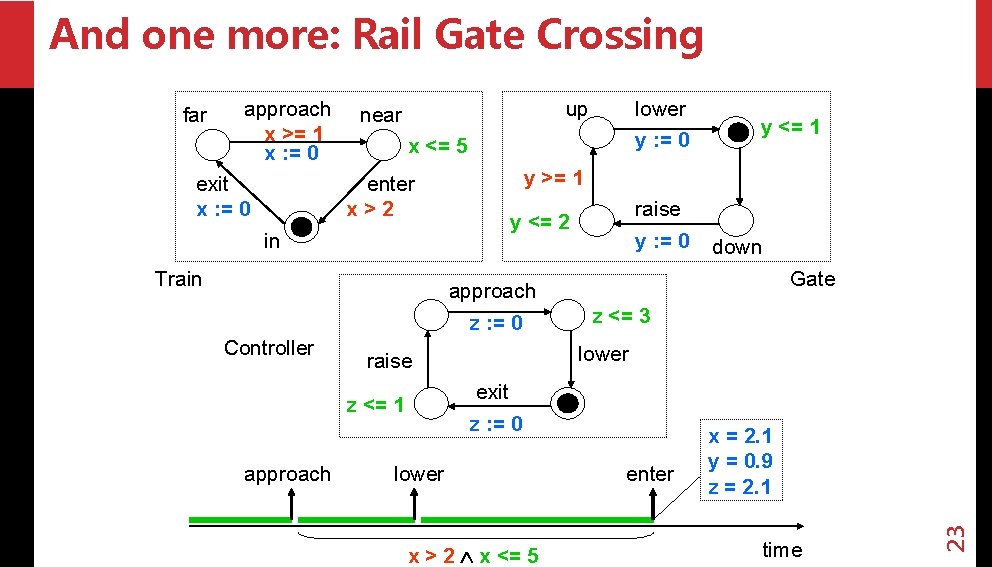
And one more: Rail Gate Crossing approach x >= 1 x : = 0 exit x : = 0 up near x <= 5 enter x>2 in Train approach raise y : = 0 y <= 2 down Gate z <= 3 lower raise exit z : = 0 z <= 1 y >= 1 approach z : = 0 Controller lower y : = 0 lower x > 2 x <= 5 enter x = 2. 1 y = 0. 9 z = 2. 1 time 23 far

Time Convergence, Timelocks, Zenoness • Not all paths in a timed automaton represent realistic behaviours. Examples… • Three essential phenomena: INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 24 • Time Convergence • Timelock • Zenoness

Time Divergence INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 25

Timelocks • For a state σ in a timed-automaton, there must be some way for time to progress. • If no way is possible, then “σ ” has a timelock. Let Pathsdiv(σ) be the set of time-divergent paths starting in σ. A state s contains a timelock iff Pathsdiv(σ) = Φ A timed automaton is timelock-free iff none of its reachable states contains a timelock. INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 26 • A timelock is a modeling flaw – should be avoided.

Zenoness An infinite path fragment π is zeno if and only if it is time-convergent and infinitely many discrete actions are executed within π. • Zeno paths represent non-realizable behaviour • since their execution would require infinitely fast processors. • Thus zeno paths are modelling flows and should be avoided. • To check whether a timed automaton is non-zeno is algorithmically difficult. e. g. , by static analysis. INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 27 • Instead, sufficient conditions are considered that are simple to check,

Verification q System modeled as a product of timed automata q Verification problem reduced to reachability or to temporal logic model checking q Applications § Real-time controllers § Asynchronous timed circuits § Scheduling § Distributed timing-based algorithms

Variants of timed automata INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 29

Timed Automata and Reachability Abstractions INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 30

Region Graphs INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 31

Standard Regions (what do the rules mean? ) INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 32 2 Clocks = 2 dimensions The partition is compatible with constraints, time elapsing and resets.

Operations on Regions (0<x=y<1) INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR (0<y<1=x) (0<y<x<1) (1<x<2, 0<y<1, {x }<{y}) (x=0, y=1) (0<x<1, y=0) (y=1<x<2) 33 (x=0, y=0)

Region Automaton INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 34

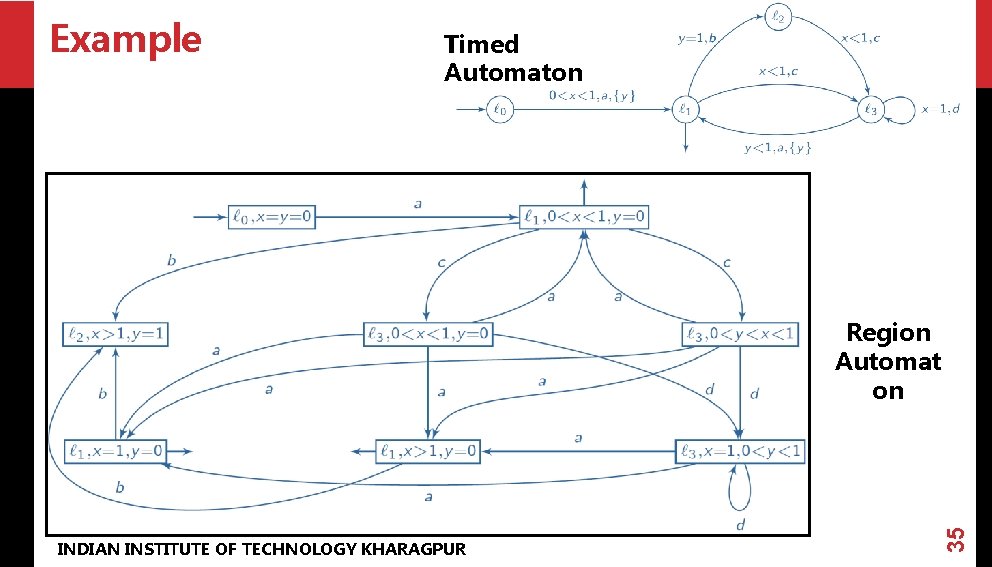
Example Timed Automaton INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 35 Region Automat on

A Logic for Timed Automata – Timed CTL INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 36

Derived Operators INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 37

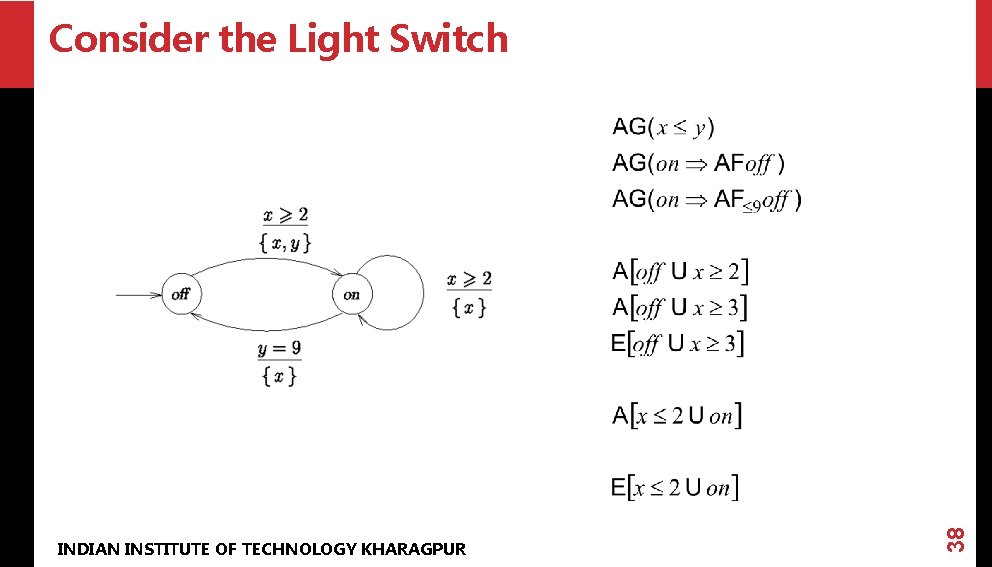
INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 38 Consider the Light Switch

Timeliness Properties AG [send(m) � AF<5 receive(m)] receive(m) always occurs within 5 time units after send(m) EG [send(m) � AF=11 receive(m)] receive(m) may occur exactly 11 time units after send(m) AG [ AG=25 putbox] INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 39 putbox occurs periodically (exactly) every 25 time units (note: other putbox’s may occur in between)

Moving forward from Timed Automata • Regular - Finite (Deterministic/Non. Deterministic Finite Automata) • Locations = States, Memory is finite – states are finite. • Discrete actions only • Transition Systems • Finite location systems : possibly infinite states (with variables) • Discrete actions only • Timed Automata • Finite location systems – timers : possibly infinite states (When would a TA have finite states? ) • Discrete and Delay actions • Hybrid Automata INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR 40 • Finite location systems – beyond timers : possibly infinite states • Discrete actions and Custom activities