Time Series Econometrics Lecture 1 Introduction to TS

Time Series Econometrics Lecture 1. Introduction to TS Analysis September 7 st , 2011

Course Information Title: Time Series (TS) Econometrics Lecturer: Renata Ivanova Language: English During lectures and exercise sessions we talk only in English! Lectures and Exercise sessions Time: Wednesday, 18: 30 – 21: 30, room T 59/T 60 Office hours: Wednesday, 17: 00 -18: 00, room T 58 Email: rivanova@cerge-ei. cz N!B! Course page: http: //home. cerge-ei. cz/Ivanova/TS. html

Course Information (Cont. ) Textbooks 1. Enders, W. (2004). Applied Econometrics: Time Series. John Wiley & Sons, Inc. 2 nd ed. 2. Kocenda, E. & Cerny, A. (2007). Elements of Time Series Econometrics: An Applied Approach. Karolinum, 2007. 3. Charemza, W. & Deadman, D. (2001). New directions in econometric practice: General to specific modeling, cointegration, and vector autoregression. Course calendar § § Lectures 1 -4 Midterm exam (beginning of October) Lectures 5 -10 Final exam

Course Policies Attendance üCompulsory attendance of all lectures and exercise sessions ü No laptops allowed during the lecture ü Taking notes is not compulsory ü Reading assignments for every class ü Late arrivals will not be tolerated ü Class participation is highly encouraged! ü Academic dishonesty (cheating) will never be tolerated Grading Your grade (100 %) = Midterm (15 %) + Final (40 %) + + Homework (40 %) + Quizzes (5 %). Final exam Winter exam session: January , 2012

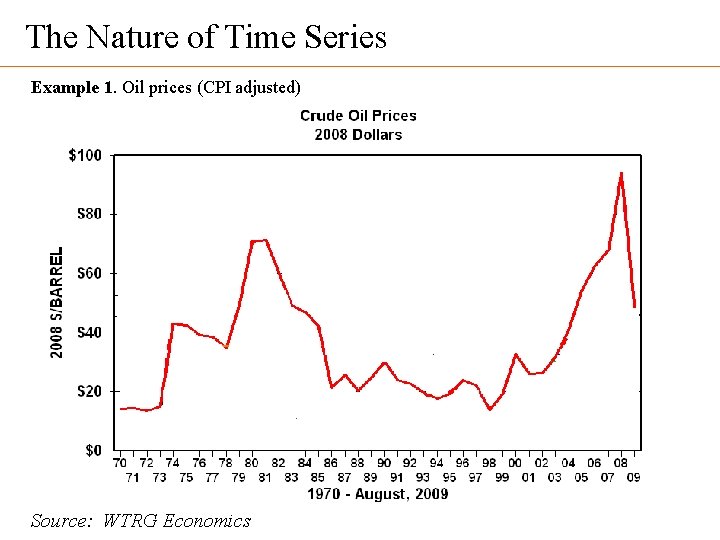
The Nature of Time Series Example 1. Oil prices (CPI adjusted) Source: WTRG Economics

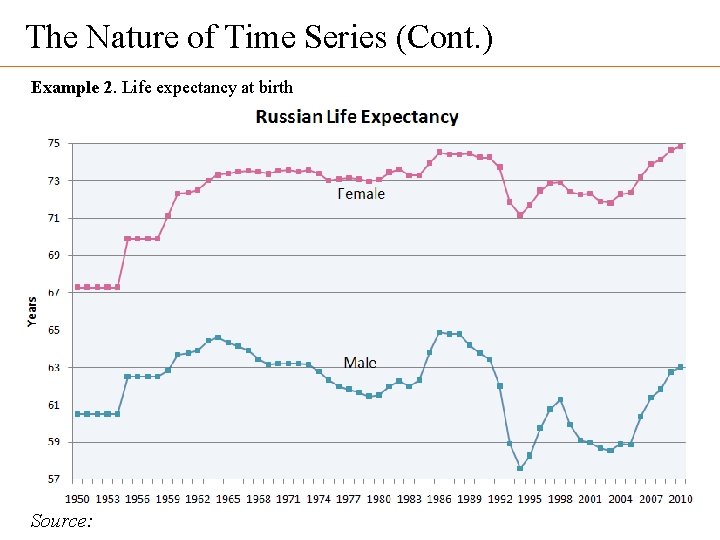
The Nature of Time Series (Cont. ) Example 2. Life expectancy at birth Source:

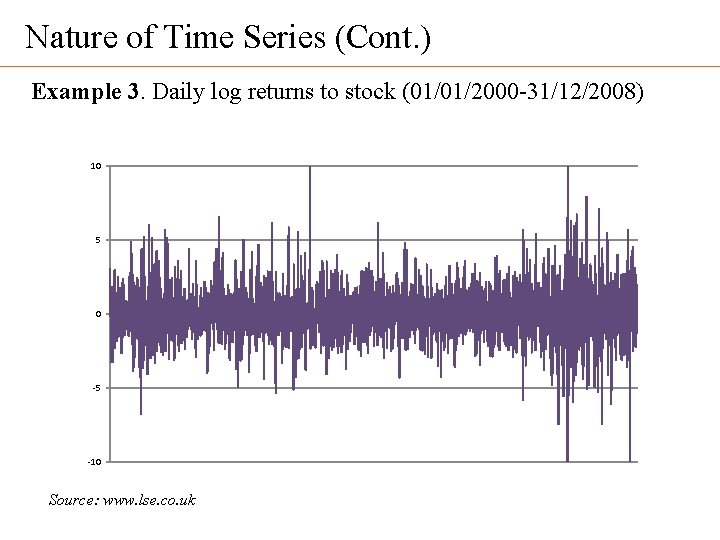
Nature of Time Series (Cont. ) Example 3. Daily log returns to stock (01/01/2000 -31/12/2008) 10 5 0 -5 -10 Source: www. lse. co. uk

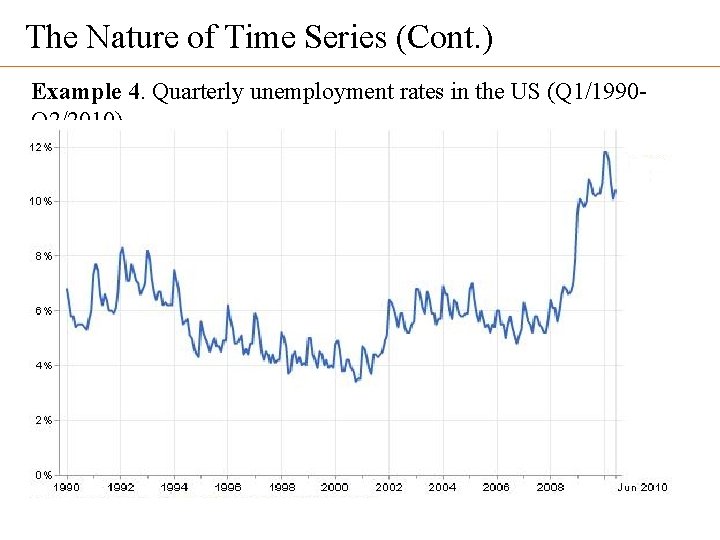
The Nature of Time Series (Cont. ) Example 4. Quarterly unemployment rates in the US (Q 1/1990 Q 2/2010)

Definition Time series : a sequence of numerical observations ordered in time TS attributes • Frequency: yearly, quarterly, monthly, weekly, daily, intra-daily - Equal spacing of observations • Time span (01/01/2000 – 31/12/2000) sample size (number of periods)

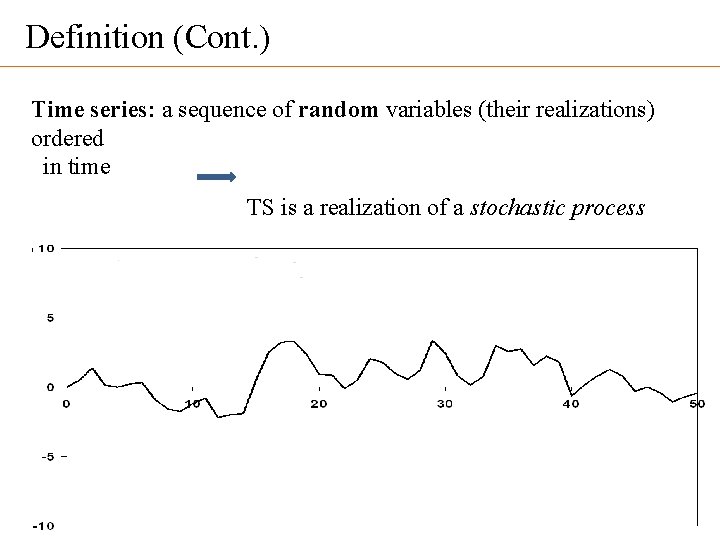
Definition (Cont. ) Time series: a sequence of random variables (their realizations) ordered in time TS is a realization of a stochastic process • A single realization

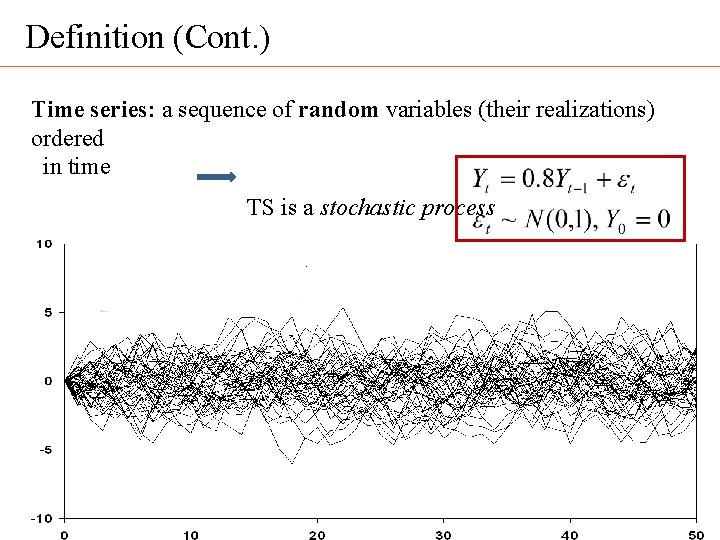
Definition (Cont. ) Time series: a sequence of random variables (their realizations) ordered in time TS is a stochastic process • 50 realizations

Definition (Cont. ) TS characteristics • Mean • Variance • Autocovariances - Subsequent elements of a TS are generally not independent

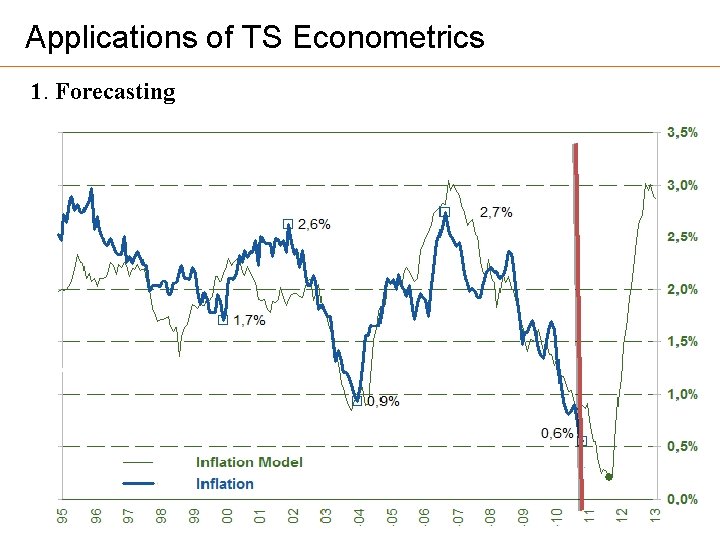
Applications of TS Econometrics 1. Forecasting

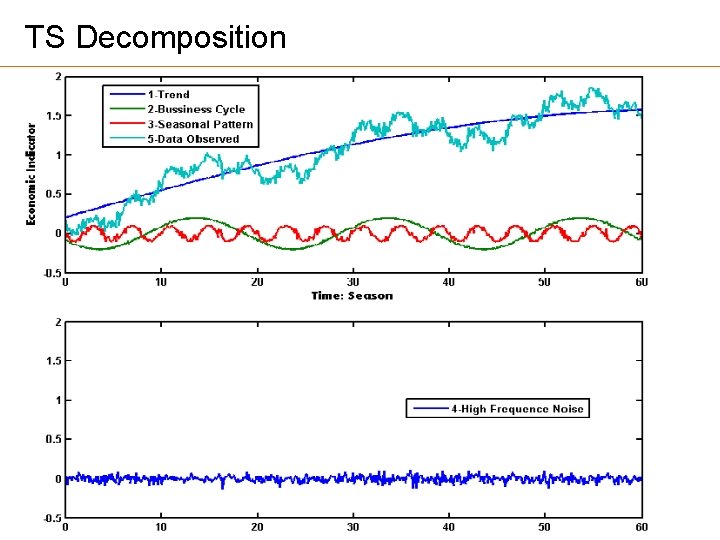
TS Decomposition

Applications of TS Econometrics (Cont. ) 2. Testing economic theory Random walk hypothesis: day-to-day changes in price of stock should have zero mean Stock price model: Hypothesis:

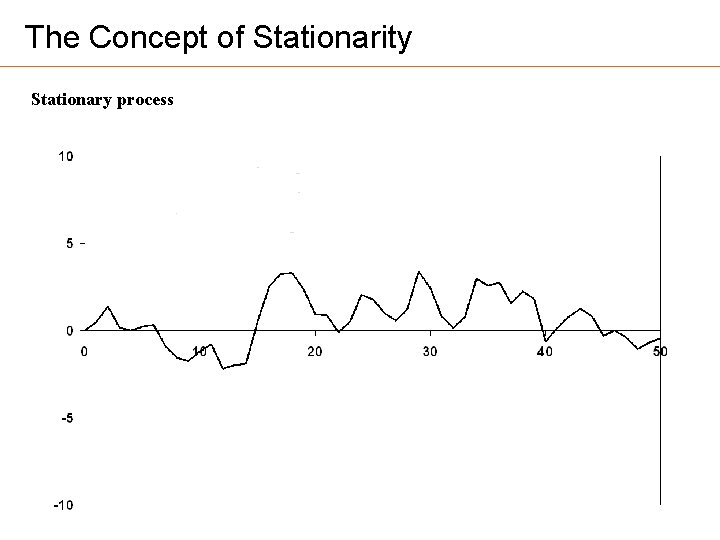
The Concept of Stationarity Stationary process

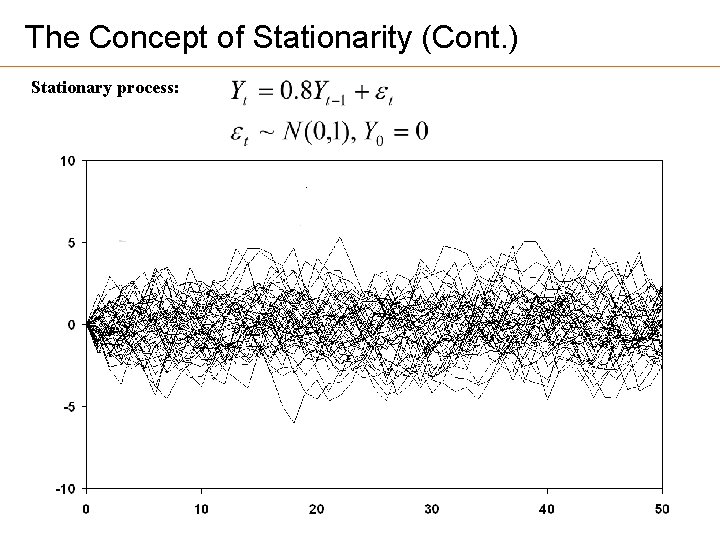
The Concept of Stationarity (Cont. ) Stationary process:

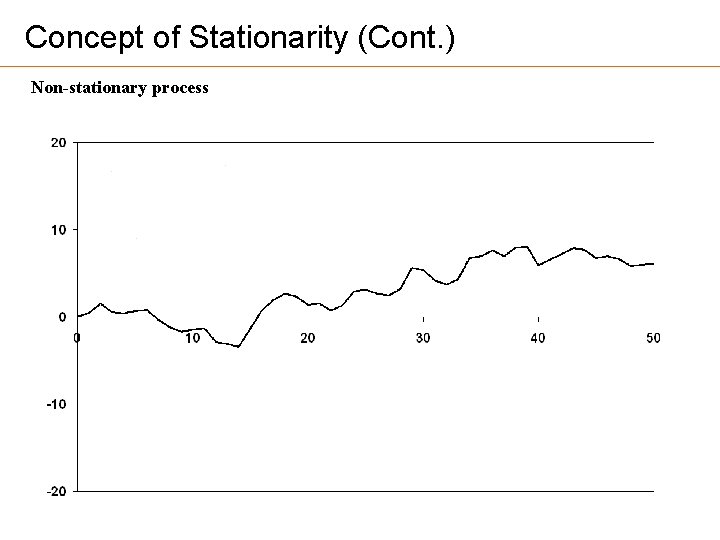
Concept of Stationarity (Cont. ) Non-stationary process

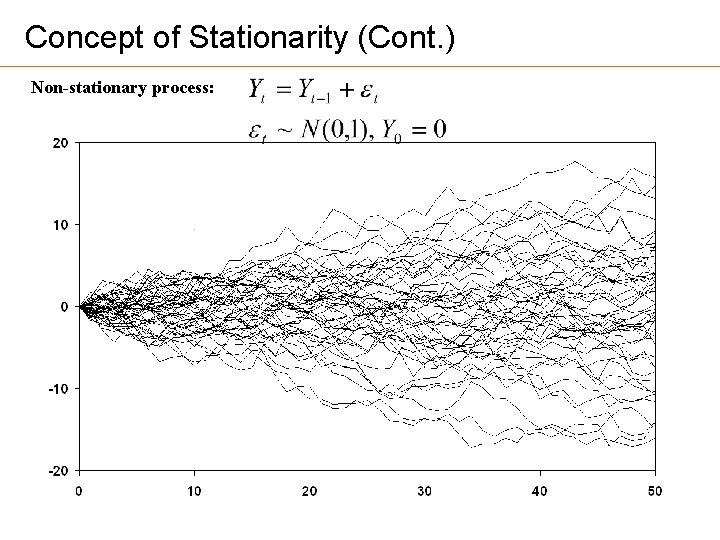
Concept of Stationarity (Cont. ) Non-stationary process:

Stationarity: Formal Definition TS is weakly (covariance) stationary if: 1. Population mean of the distribution is independent of time TS often returns to its initial value 2. Population variance of the distribution is independent of time TS is homoskedastic 3. Autocovariances Covariance depends only on k, not on t Strong stationarity – Same distribution shape (all moments are

The Concept of Stationarity (Cont. ) • Example Is { } a stationary process? Stationarity conditions Answer: Yes White Noise

Detecting Stationarity: ACF Autocovariance - covariance of a variable with itself in another point of time Autocorrelation For a stationary TS { } Autocorrelation function (ACF)

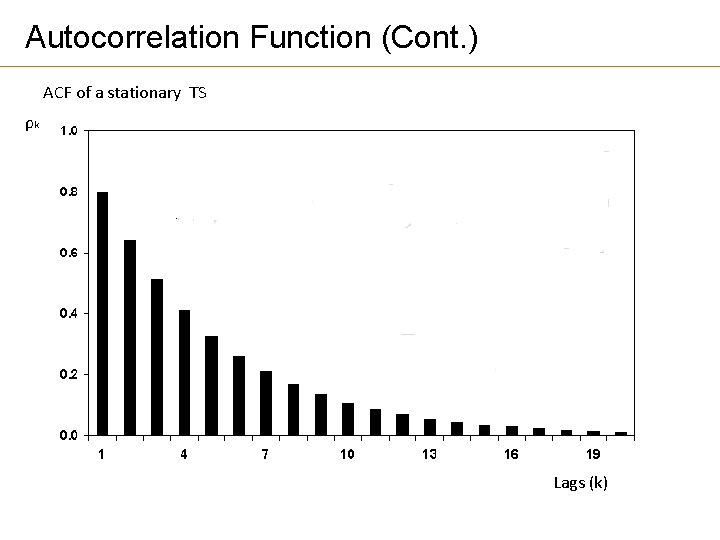
Autocorrelation Function (Cont. ) ACF of a stationary TS ρk Lags (k)

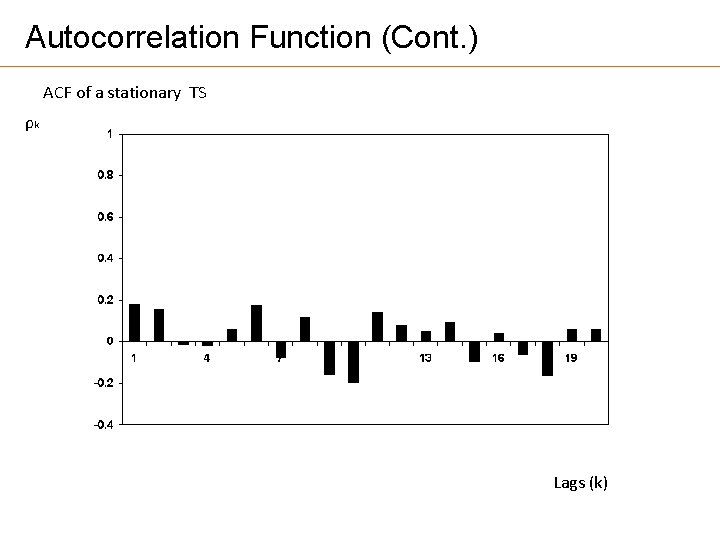
Autocorrelation Function (Cont. ) ACF of a stationary TS ρk Lags (k)

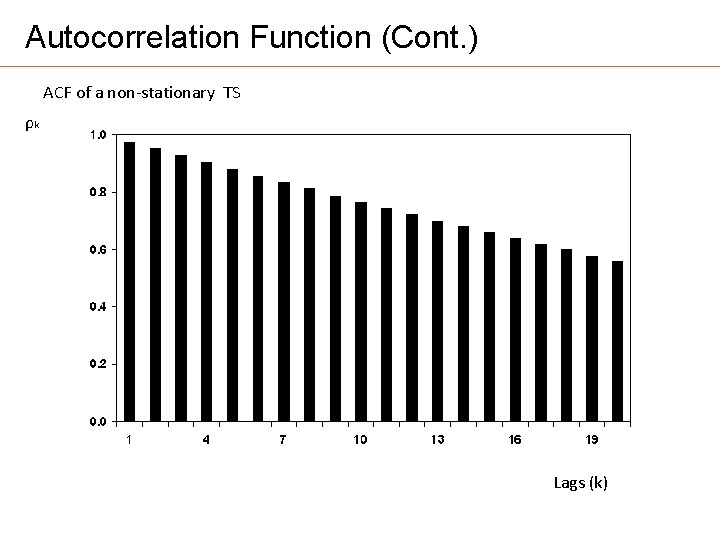
Autocorrelation Function (Cont. ) ACF of a non-stationary TS ρk Lags (k)

Autocorrelation Function (Cont. ) Properties of AFC