Time Series Econometrics Analysis of Nonstationary Data Outline

Time Series Econometrics Analysis of Nonstationary Data Outline • Introduction • Stationarity and Unit Root • Analysis of Nonstationary Data

Introduction • A sequence of random variables is called stochastic process. • A particular realization of the stochastic process is called time series. • Hence, time series is generated by a stochastic or random process. • As sample is to a population in cross section data, realization (time series) is to a random process.

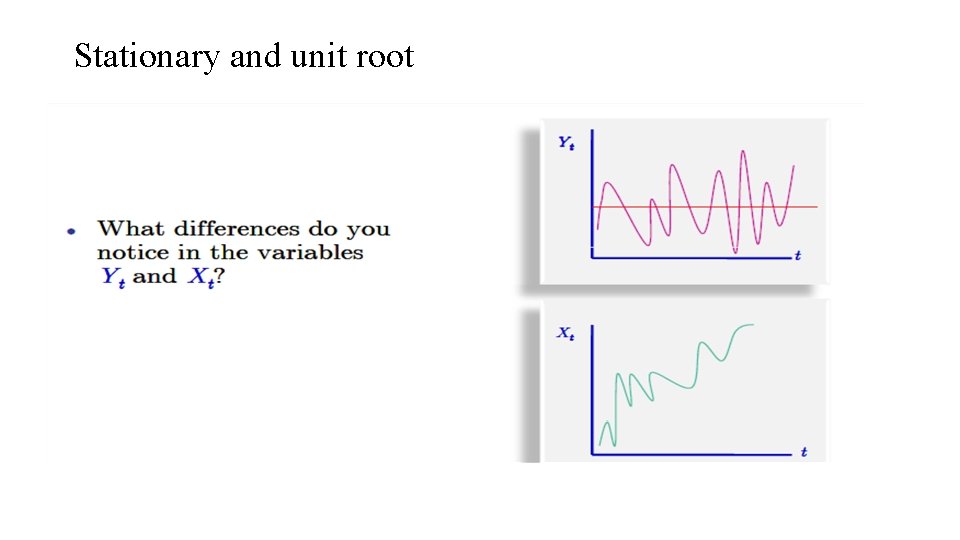
Stationary and unit root

Stationary and unit root

Stationary and unit root

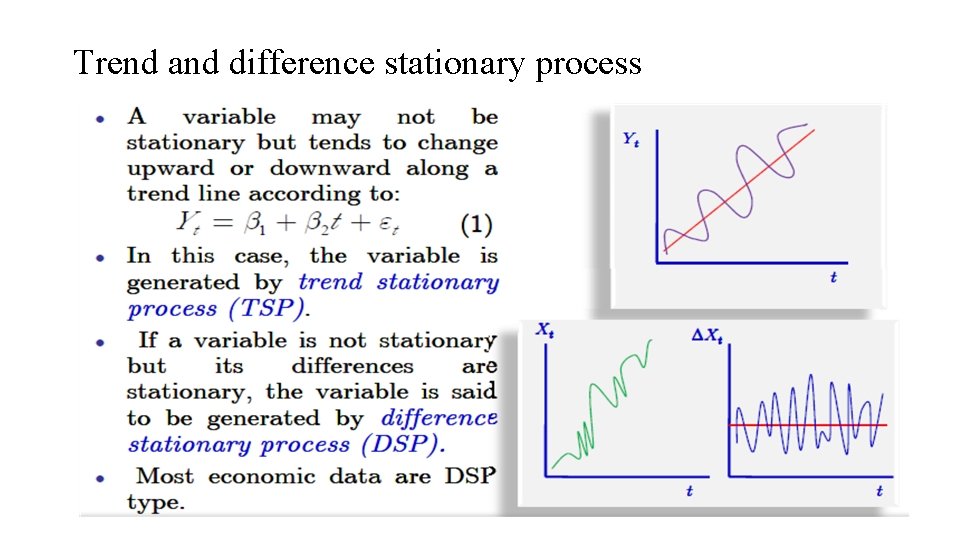
Trend and difference stationary process

Non-stationary time series

Non-stationary time series

Non-stationary time series

Integrated time series

Integrated time series

Spurious regression

Spurious regression

Test of stationarity: unit root

Test of stationarity: unit root

Test of stationarity: unit root

Test of stationarity:

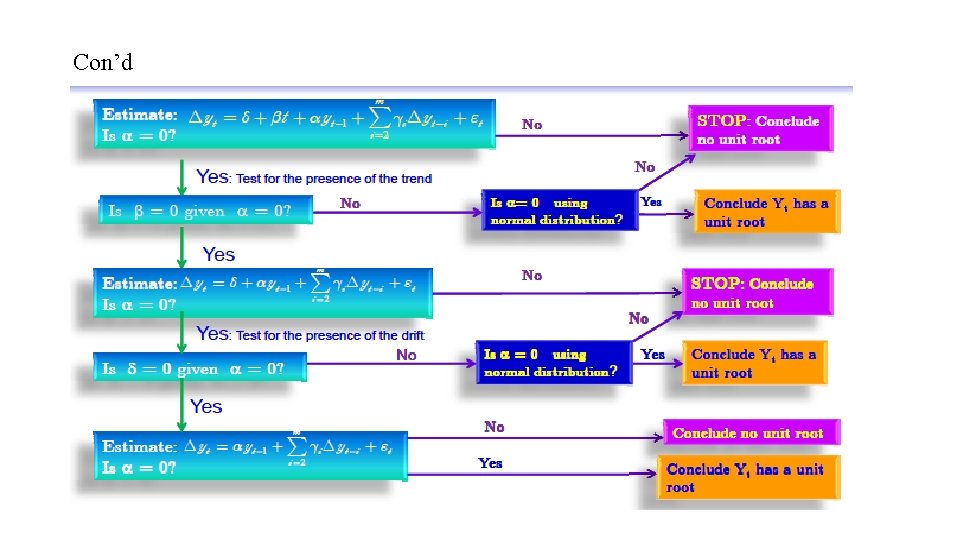
Con’d

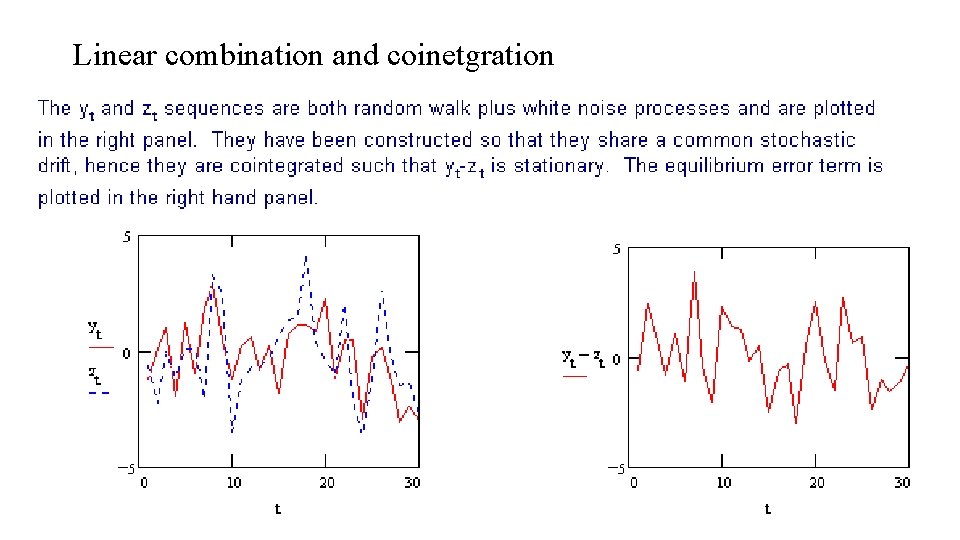
Linear combination and coinetgration • If the time series variables under consideration, Y and X, are the same order of integration though they are individually non stationary, the estimation of regression equation of Y on X or X on Y in level form [or static form] by OLS method is referred to as cointegration regression. • Inshort if the linear combination of non-stationary series is stationary we can say that there is cointegraion. • If two or more series are individually integrated but some linear combination of them has a lower order of integration, then the series are said to be cointegrated. • A common example is where the individual series are first-order integrated (I(1)) but some (cointegrating) vector of coefficients exists to form a stationary linear combination of them.

Linear combination and coinetgration • If there exists a stationary linear combination of nonstationary random variables, the variables combined are said to be cointegrated. • The old woman and the boy are unrelated to one another, except that they are both on a random walk in the park. Information about the boy's location tells us nothing about the old woman's location. • The old man and the dog are joined by one of those leashes that has the cord rolled up inside the handle on a spring. Individually, the dog and the man are each on a random walk. They cannot wander too far from one another because of the leash. We say that the random processes describing their paths are cointegrated.

Linear combination and coinetgration

The Engle-Granger Methodology

Con’d

Con’d

Con’d