Time Complexity We use a multitape Turing machine

Time Complexity • We use a multitape Turing machine • We count the number of steps until a string is accepted • We use the O(k) notation 1

Example: Algorithm to accept a string : • Use a two-tape Turing machine • Copy the • Compare the on the second tape and 2

Time needed: • Copy the on the second tape • Compare the and Total time: 3

For string of length time needed for acceptance: 4

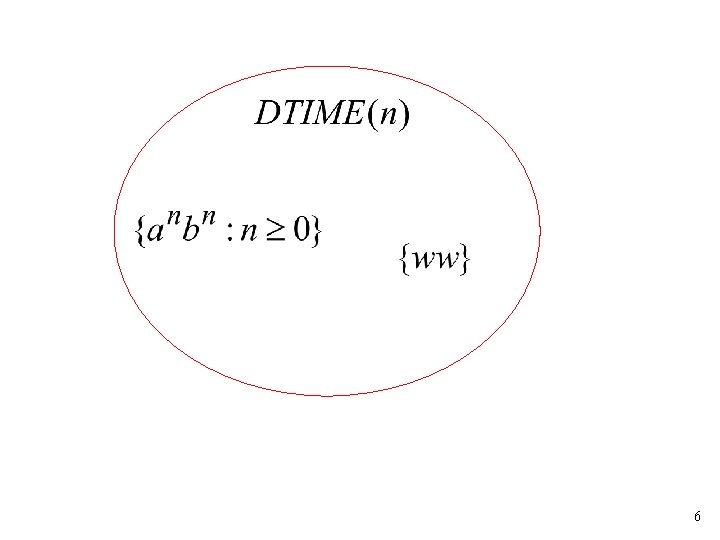
Language class: A Deterministic Turing Machine accepts each string of length in time 5

6

In a similar way we define the class for any time function: Examples: 7

Example: The membership problem for context free languages (CYK - algorithm) Polynomial time 8

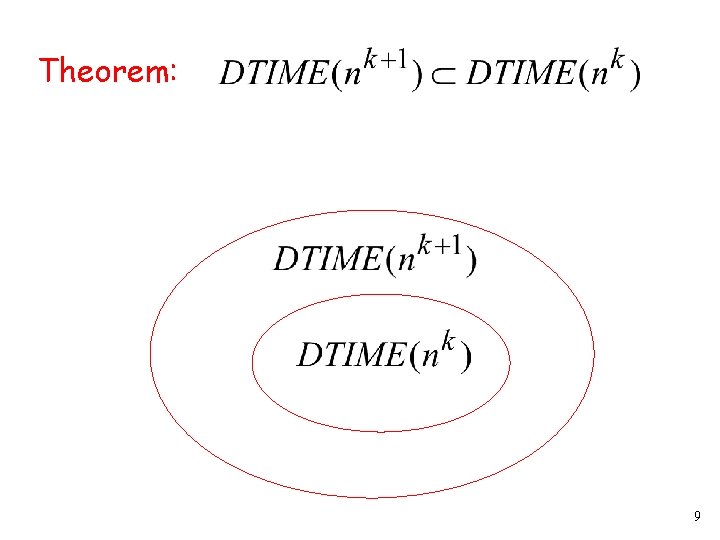
Theorem: 9

Polynomial time algorithms: Represent tractable algorithms: For small we can compute the result fast 10

The class for all • Polynomial time • All tractable problems 11

CYK-algorithm 12

Exponential time algorithms: Represent intractable algorithms: Some problem instances may take centuries to solve 13

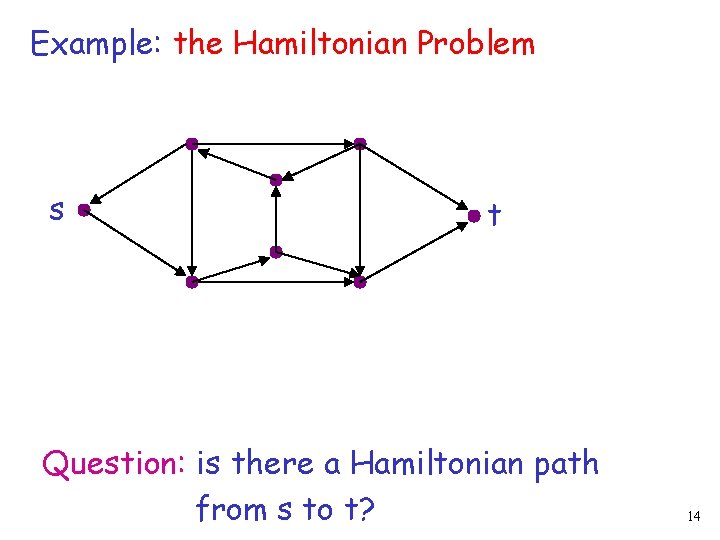
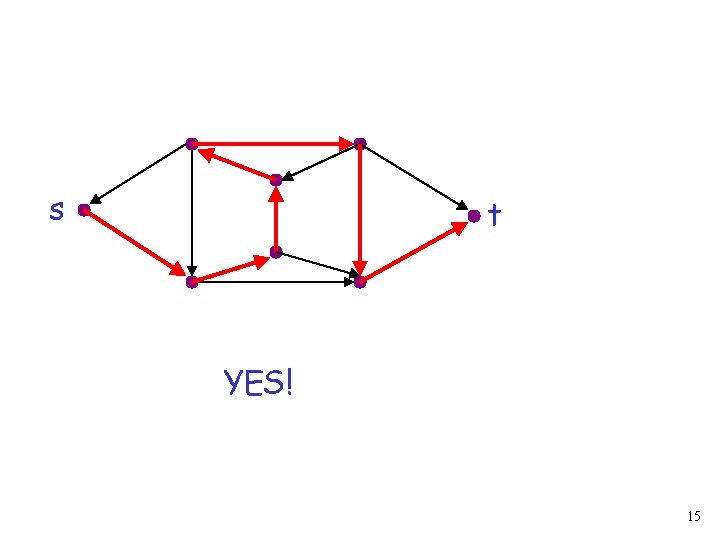
Example: the Hamiltonian Problem s t Question: is there a Hamiltonian path from s to t? 14

s t YES! 15

A solution: search exhaustively all paths L = {<G, s, t>: there is a Hamiltonian path in G from s to t} Exponential time Intractable problem 16

Example: The Satisfiability Problem Boolean expressions in Conjunctive Normal Form: Variables Question: is expression satisfiable? 17

Example: Satisfiable: 18

Example: Not satisfiable 19

For variables: exponential Algorithm: search exhaustively all the possible binary values of the variables 20

Non-Determinism Language class: A Non-Deterministic Turing Machine accepts each string of length in time 21

Example: Non-Deterministic Algorithm to accept a string : • Use a two-tape Turing machine • Guess the middle of the string and copy on the second tape • Compare the two tapes 22

Time needed: • Use a two-tape Turing machine • Guess the middle of the string and copy on the second tape • Compare the two tapes Total time: 23

24

In a similar way we define the class for any time function: Examples: 25

Non-Deterministic Polynomial time algorithms: 26

The class for all Non-Deterministic Polynomial time 27

Example: The satisfiability problem Non-Deterministic algorithm: • Guess an assignment of the variables • Check if this is a satisfying assignment 28

Time for variables: • Guess an assignment of the variables • Check if this is a satisfying assignment Total time: 29

The satisfiability problem is an - Problem 30

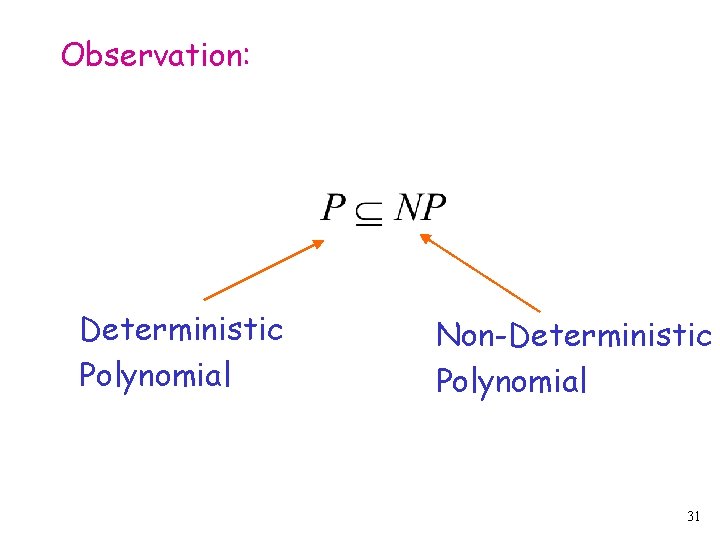
Observation: Deterministic Polynomial Non-Deterministic Polynomial 31

Open Problem: WE DO NOT KNOW THE ANSWER 32

Open Problem: Example: Does the Satisfiability problem have a polynomial time deterministic algorithm? WE DO NOT KNOW THE ANSWER 33