Time Complexity for Loops CSE 2320 Algorithms and

Time Complexity for Loops CSE 2320 – Algorithms and Data Structures Alexandra Stefan University of Texas at Arlington 6/5/2021 1

Summary & Conventions • On Time complexity of for loops – Time complexity: T(N), T(N, M) – What is the problem size? (See n = right-left+1 example) – Table method (table “follows” loop execution) • Important to use it when the iterations of the inner loop depend on the variable of the outer loop. – Tricky loops • An instruction is a method call => do not count it as 1 instruction. See time complexity of method • 3 level nested loops – Big-Oh briefly – understanding why we only look at the dominant term • Terminology and notation: – 1 -> N will stand for 1, 2, 3, 4, …(N-1), N – log 2 N = lg N – Use interchangeably: • Runtime and time complexity • Record and item 2

Code -> detailed count -> Dominant term • Write a piece of code that builds an array by inserting a new element every time and keeping the array in sorted order after each insertion: – Easier problem: insert an element in a sorted array (assume the array has enough space to hold the new item as well. You can just update the size variable. ) • Count (in detail) how many times specific instructions are executed. • Look at the contribution of N 2 vs 50 N for large values of N • – If one instruction executes in 10 -9 seconds, how long do N 2 and 50 N take? . In future examples to analyze code, I will remove the task oriented parts and keep the loop structure. • Other examples – Find the index of the smallest item in an array. Next, place the smallest item on the first position by swapping it with the first item in the array – Write a piece of code that returns 1/0 if all numbers in an array are unique or not. 3

How many times does the instruction printf("B ") execute? Worksheet (The number of executions of printf("B ") will determine the time complexity of this code. We will discuss time complexity formally later on. ) // Example A 1. for (i = 1; i<=7; i++) { printf("n. A: "); for(k=1; k<=5; k = k+1) printf("B "); } // Example A 2. Replace hardcoded value 7 and 5 with variables N and M for (i = 1; i<=N; i++) { printf("n. A: "); for(k=1; k<=M; k = k+1) printf("B "); } 4

How many times does the instruction printf("B ") execute? Answers (The number of executionss of printf("B ") will determine the time complexity of this code. We will discuss time complexity formally later on. ) // Example A 1. for (i = 1; i<=7; i++) { printf("n. A: "); for(k=1; k<=5; k = k+1) printf("B "); //// Answer: 35 = 7*5 } //Example A 2. Replace hardcoded value 7 and 5 with variables N and M. for (i = 1; i<=N; i++) { printf("n. A: "); for(k=1; k<=M; k = k+1) printf("B "); /////// Answer: N*M } Since the expression that gives the count now depends on N and M, lets be more formal and use the notation : T(N, M) = Θ(N*M) We use T(N, M) to indicate that it is a function of N and M, and use Θ to indicate that it is not the exact count of instructions, but the time complexity of the code. 5

Using the TABLE METHOD to derive this complexity: Output of Example A 1: // Example A 1. A: B B B for (i = 1; i<=7; i++) { A: B B B B B printf("n. A: "); for(k=1; k<=5; k = k+1) A: B B B B B printf("B "); A: B B B } A: B B B // Example A 2. Replace hardcoded value 7 and 5 with variables N and M for (i = 1; i<=N; i++) { printf("n. A: "); for(k=1; k<=M; k = k+1) printf("B "); } Iteration of outer loop How many times does the instruction printf("B ") execute? Worksheet i printf(B) Repetitions Is executed when k takes values: of printf(B) (count of different values of k) 1 st 1 1, 2, 3, 4, 5 5 2 nd 2 1, 2, 3, 4, 5 5 3 rd 3 1, 2, 3, 4, 5 5 4 th 4 1, 2, 3, 4, 5 5 5 th 5 1, 2, 3, 4, 5 5 6 th 5 1, 2, 3, 4, 5 5 7 th 5 1, 2, 3, 4, 5 5 Total: 5+5+5+5 = 7*5 = 35 Adding all the terms in the rightmost column will give the time complexity. 35 is the final result. Common error: take this result (35) and multiply it by 7 again. WRONG! 6

Using the TABLE METHOD to derive this complexity: // Example A 1. for (i = 1; i<=7; i++) { printf("n. A: "); for(k=1; k<=5; k = k+1) printf("B "); } // Example A 2. Replace hardcoded value 7 and 5 with variables N and M Output of Example A 1: for (i = 1; i<=N; i++) { A: B B B printf("n. A: "); A: B B B B B for(k=1; k<=M; k = k+1) A: B B B printf("B "); A: B B B } A: B B B B B Iteration of outer loop How many times does the instruction printf("B ") execute? Worksheet i printf(B) Repetitions Is executed when k takes values: of printf(B) (count of different values of k) 1 st 1 1, 2, 3, 4, …, M M 2 nd 2 1, 2, 3, 4, …, M M 3 rd 3 1, 2, 3, 4, …, M M … … ith i 1, 2, 3, 4, …, M M … … (N-1)th N-1 1, 2, 3, 4, …, M M Nth N 1, 2, 3, 4, …, M M Total: M+M+M+…M = N*M = NM Adding all the terms in the rightmost column will give the time complexity. NM is the final result. Common error: take this result (NM) and multiply it by N again. WRONG! 7

How many times does the instruction printf("B ") execute? Worksheet // Example A 3. for (i = 1; i<=5; i++) { // i goes up to 5 printf("n. A: "); for(k=i; k<=5; k = k+1) // k starts at value i (inner loop iterations depend on value of outer loop variable) printf("B "); } What is the output of this code? Use a table to help you count the repetitions of printf(B "). 8

How many times does the instruction printf("B ") execute? Answer Output of Example A 3: A: B B B A: B B A: B The table on the right helps us count the number of executions of printf("B "). i Iteration of outer loop // Example A 3. T(N) = …. for (i = 1; i<=5; i++) { // i goes up to 5 printf("n. A: "); for(k=i; k<=5; k = k+1) // here k starts at value i printf("B "); } printf(B) Is executed when k takes values: Repetitio ns of printf(B) (count of different values of k) 1 st 1 1, 2, 3, 4, 5 5 2 nd 2 2, 3, 4, 5 4 3 rd 3 3, 4, 5 3 4 th 4 4, 5 2 5 th 5 5 1 Total: 5+4+3+2+1 = 5*(5+1)/2 (This is a summation of part of an arithmetic Series. ) 9

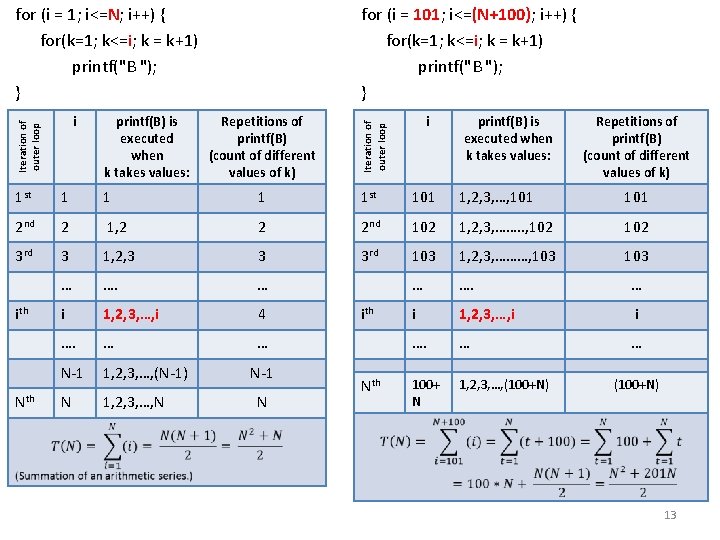
How many times does the instruction printf("B ") execute? Worksheet i Example A 4. Replace hardcoded value 5 with variable N. Goal: e able to generalize and understand the loop’s pattern of behavior. printf(B) Is executed when k takes values: Repetitions of printf(B) (count of different values of k) for (i = 1; i<=N; i++) { printf("n. A: "); for(k=i; k<=N; k = k+1) printf("B "); } 10

How many times does the instruction printf("B ") execute? Answer for (i = 1; i<=N; i++) { printf("n. A: "); for(k=i; k<=N; k = k+1) printf("B "); } Iteration of outer loop Example A 4. Replace hardcoded value 5 with variable N. Goal: generalize and understand the loop’s pattern of behavior. i printf(B) is executed when k takes values: Repetitions of printf(B) (count of different values of k) 1 1, 2, 3, …, N N 2 2, 3, …, N N-1 3 3, …, N N-2 … …. i i, i+1, …, N …. … … N-1 (N-1), N 2 N N 1 … N+1 -i 11

“independent” and “dependent” nested loops for (i = 1; i<=N; i++) { // N iterations for(k=1; k<=M; k = k+1) // M iterations printf("B "); } “Independent” loops: the number of iterations of the k loop does not depend on values of the variable of the outer loop, i. => You can just multiply the repetitions of the two loops: T(N, M) = N*M for (i = 101; i<=(100+N); i++) { // N iterations for(k=1; k<=M; k = k+1) // M iterations printf("B "); } “Independent” loops: the number of iterations of the k loop does not depend on values of the variable of the outer loop, i. => You can just multiply the repetitions of the two loops (values of i do not matter) T(N, M) = N*M for (i = 1; i<=N; i++) { // N iterations for(k=1; k<=i; k = k+1) // i iterations printf("B "); } “DEPENDENT” loops: the number of iterations of the k loop depends on values of the variable of the outer loop, i. => MAKE THE TABLE for (i = 101; i<=(100+N); i++) { // N iterations for(k=1; k<=i; k = k+1) // i iterations printf("B "); } “DEPENDENT” loops: the number of iterations of the k loop depends on values of the variable of the outer loop, i. => MAKE THE 12 TABLE

Iteration of outer loop i printf(B) is executed when k takes values: for (i = 101; i<=(N+100); i++) { for(k=1; k<=i; k = k+1) printf("B "); } Repetitions of printf(B) (count of different values of k) i Iteration of outer loop for (i = 1; i<=N; i++) { for(k=1; k<=i; k = k+1) printf("B "); } printf(B) is executed when k takes values: Repetitions of printf(B) (count of different values of k) 1 st 101 1, 2, 3, …, 101 2 nd 2 1, 2 2 2 nd 102 1, 2, 3, ……. . , 102 3 rd 3 1, 2, 3 3 3 rd 103 1, 2, 3, ………, 103 … …. … i 1, 2, 3, …, i 4 i 1, 2, 3, …, i i …. … … N-1 1, 2, 3, …, (N-1) N 1, 2, 3, …, N 100+ N 1, 2, 3, …, (100+N) ith N-1 N ith Nth (100+N) 13

Time complexity as a function of more than one variable // Write the Θ (Theta) time complexity for (i=0; i<N; i++) for (k=0; k<N; k++) printf("B"); for (i=0; i<M; i++) printf("A"); // Write the Θ (Theta) time complexity for (i=0; i<N; i++) for (k=0; k<M; k++) printf("B"); for (i=0; i<M; i++) printf("A"); Contribution from both loops: Dominant term: Θ(______________) T(N, M) = …. . 14

Time complexity as a function of more than one variable // Write the Θ (Theta) time complexity for (i=0; i<N; i++) for (k=0; k<N; k++) printf("B"); for (i=0; i<M; i++) printf("A"); // Write the Θ (Theta) time complexity for (i=0; i<N; i++) for (k=0; k<M; k++) printf("B"); for (i=0; i<M; i++) printf("A"); N 2+M => Θ(N 2+M) Must keep both. We do not know that N 2 > M T(N, M) = …. . NM+M => Θ(NM) We know that NM > M T(N, M) = …. . 15

Geometric progressions in a loop // Example D. T(N) = log 5(N) for(i=1; i<=N; i = i*5) printf("A"); How many powers of 5 smaller or equal than N are there? 50, 51, …, 5 p ( where 5 p <=N< 5 p+1 ) We want p. Simplify by assuming: N = 5 p, take log 5 on both sides: log 5(N) = log 5 (5 p) => log 5(N) = p*log 5 (5) => log 5(N) = p Because of our simplification we may be off by a constant (i. e. the exact answer is (p-1) or (p+1)). The missing ‘-1’ or ‘+1’ will generate lower-order terms => will not change the dominant term or the Θ. 16

Table Method for Time Complexity // Example D. T(N) = …. for (i = 1; i<=N; i++) for(k=1; k<=N; k = k*2) printf("A"); 17

Table Method – for Time Complexity i // Example D. T(N) = …. for (i = 1; i<=N; i++) for(k=1; k<=N; k = k*2) printf("A"); How many powers of 2 smaller or equal than N are there? 20, 21, …, 2 p ( where 2 p <=N< 2 p+1 ) We want p. Simplify by assuming: N = 2 p, => p = lg. N. Here: lg. N=log 2 N Because of our simplification we may be off by a constant (i. e. the exact answer is (p-1) or (p+1)). The missing ‘-1’ or ‘+1’ will generate lower-order terms => will not change the dominant term or the Θ. Self check: Use ((lg. N )- 2) in the last columns and verify that the dominant term and Θ are still the same. k takes values: Iterations of ‘for k’ for this i 1 1, 2, 4, 8, 16 , …, 2 p where 2 p is the largest power of 2 less or equal to N 2 1, 2, 4, 8, 16 , …, 2 p ~lg. N i 1, 2, 4, 8, 16 , …, 2 p ~lg. N … … N-1 1, 2, 4, 8, 16 , …, 2 p ~lg. N N 1, 2, 4, 8, 16 , …, 2 p ~lg. N … … 18

Table Method for Time Complexity // Example D. T(N) = …. for (i = 1; i<=N; i++) for(k=1; k<=i; k = k*2) printf("A"); 19

Table Method – for Time Complexity i // Example E. T(N) = …. for (i = 1; i<=N; i++) for(k=1; k<=i; k = k*2) printf("A"); How many powers of 2 smaller than i are there? 20, 21, …, 2 p ( where 2 p <=i< 2 p+1 ) We want p. Simplify by assuming: i = 2 p => p = lgi. Here: lgi=log 2 i Because of our simplification we may be off by a constant (i. e. the exact answer is (p-1) or (p+1)). The missing ‘-1’ or ‘+1’ will generate lower-order terms => will not change the dominant term or the Θ. Self check: Use ((lgi )- 2) in the last columns and verify that the dominant term and Θ are still the same. k takes values: Iterations of ‘for k’ for this i 1 1 2 1, 2 2 3 1, 2 2 4 1, 2, 4 3 i 1, 2, 4, 8, 16 , …, 2 p lgi … … … N-1 1, 2, 4, 8, 16 , …, 2 p ~lg(N-1) N 1, 2, 4, 8, 16 , …, 2 p ~lg. N 1 … 20

Time complexity // Example C (source: Dr. Bob Weems) T(N) = … for (i = 0; i<N; i++) for(k=1; k<N; k = k+k) printf("A"); -------------------------------// Example D. T(N) = …. for (i = 0; i<N; i++) for(k=1; k<N; k = k*2) printf("A"); -------------------------------// Example E. T(N) = …. for (i = 0; i<N; i++) for(k=N; k>=1; k = k/2) printf("A"); -------------------------------// Example F. T(N) = …. for (i = 0; i<N; i++) for(k=1; k<N; k = k+2) printf("A"); Practice 21

Time complexity Answers Here we can easily solve without a table because the number of k values does not depend on i, so it is the same for every iteration of the outer loop. // Example C (source: Dr. Bob Weems) T(N) = … for (i = 0; i<N; i++) N Θ(Nlg. N) for(k=1; k<N; k = k+k) k: 1, 2, 4, 8, 16, 32 …, last power of 2 smaller than N printf("A"); Geometric progression (powers of 2) => lg. N values (not exact) -------------------------------// Example D. T(N) = …. for (i = 0; i<N; i++) N Θ(Nlg. N) for(k=1; k<N; k = k*2) k: 1, 2, 4, 8, 16, 32 …, last power of 2 smaller than N printf("A"); Geometric progression (powers of 2) => lg. N values (not exact) -------------------------------// Example E. T(N) = …. for (i = 0; i<N; i++) N Θ(Nlg. N) for(k=N; k>=1; k = k/2) k: N, N/2, N/4, N/8, …, 8, 4, 2, 1 printf("A"); --------------------- Geometric progression (/2) => (1+lg. N) values (not exact) // Example F. T(N) = …. for (i = 0; i<N; i++) N 2) Θ(N for(k=1; k<N; k = k+2) k: 1, 3, 5, 7, 9, …, last odd smaller than N printf("A"); 22 Arithmetic progression (+2) => N/2 values (not exact)

Time complexity: T(n) notation Worksheet We will use T(n) to refer to the time complexity of a piece of code that depends on some value, n. If the code depends on more values, those will also be arguments of T. E. g. : T(n, m). Also n may depend on other values. // Write the Θ (Theta) time complexity for (i=left; i<right; i++) printf("A"); for (i=0; i<p; i++) { for (k=0; k<r; k++) printf("B"); } 23

Time complexity: T(n) notation Answer We will use T(n) to refer to the time complexity of a piece of code that depends on some value, n. If the code depends on more values, those will also be arguments of T. E. g. : T(n, m). // Write the Θ (Theta) time complexity for (i=left; i<right; i++) printf("A"); for (i=0; i<p; i++) { for (k=0; k<r; k++) printf("B"); } ‘for i’ loop depends on value (right-left) => Let n = (right-left) Now the code piece depends on: n, p and r => For its time complexity use: T(n, p, r) Solve: T(n, p, r) = Θ(n+pr) 24

Loops: Sequential vs Nested and Multiple Variables We keep both the n term and the pr term because we assume n, p, r to be independent, positive integers. (We cannot and must assume that n will be less than pr. In some cases n can be much bigger than pr and it will be the dominant term. ) // Write the Θ (Theta) time complexity n for (i=0; i<n; i++) printf("A"); for (i=0; i<p; i++) p for (k=0; k<r; k++) printf("B"); Θ(n + pr) r T(n, p, r) = Θ(n+pr) 25

Dominant Terms for Functions of Multiple Variables. • Give the Theta for the function below 27 n 4 m + 6 n 3 + 7 nm 2 + 100 = Θ(…………) 26

Dominant Terms for Functions of Multiple Variables. • Give the Theta for the function below 27 n 4 m + 6 n 3 + 7 nm 2 + 100 = Θ ( n 4 m + nm 2 ) m and n are independent. (m can be much larger than n. ) 27

Adding Terms (table method) for ‘dependent’ loops Cannot multiply. The values that k takes depend on i => the number of iterations of ‘for k’ is different for every i => MUST explicitly add them. for (i = 0; i<(n-1); i++) for(k=i+1; k<n; k = k+1) printf("A"); i k takes values: Iterations of ‘for k’ for this i 0 1 -> (n-1) n-1 1 2 -> (n-1) n-2 i (i+1) -> (n-1) n-i-1 … … … n-3 (n-2) -> (n-1) 2 n-2 (n-1) -> (n-1) 1 … Steps: - Table - T(…)= Summation (based on table) - Closed form - Dominant term: - Θ (Theta): Θ(n 2) If you add the individual terms (counts of repetitions of the ‘for k’ loop), you must NOT multiply by n anymore. The addition is already factoring in the contribution of the outer loop (each row corresponds to an i). T(n) : 28

Adding Terms (table method) for ‘simple’ codei k takes The table method can be applied to the simple code (with ‘independent’ loops): for (i = 0; i<n; i++) for(k=1; k<n; k = k+1) printf("A"); Steps: - Table - T(…)=Summation (based on table) - Closed form - Dominant term: - Θ (Theta): Θ(n 2) Again, since you add the individual terms, you must NOT multiply by n anymore. The addition is already factoring in the contribution of the outer loop (each row corresponds to an i). values: # Iterations of ‘for k’ for this i 0 1 -> (n-1) n-1 1 1 -> (n-1) n-1 … … i 1 -> (n-1) … … n-3 1 -> (n-1) n-1 … T(n) : 29

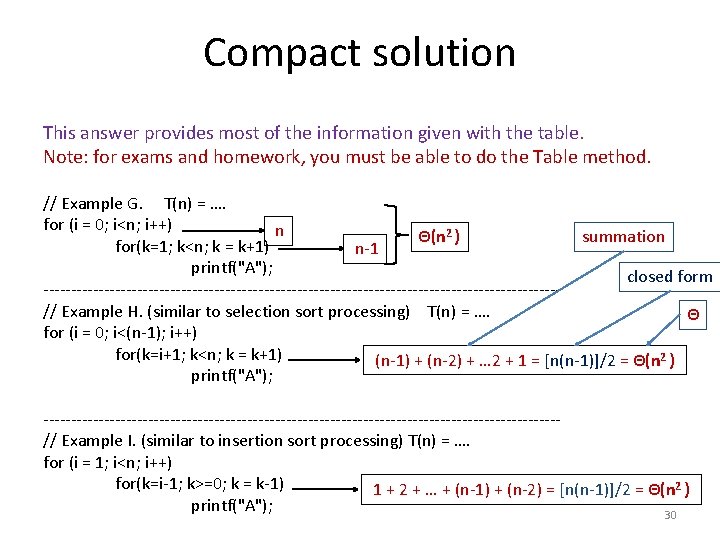
Compact solution This answer provides most of the information given with the table. Note: for exams and homework, you must be able to do the Table method. // Example G. T(n) = …. for (i = 0; i<n; i++) n Θ(n 2 ) summation for(k=1; k<n; k = k+1) n-1 printf("A"); closed form -----------------------------------------------// Example H. (similar to selection sort processing) T(n) = …. Θ for (i = 0; i<(n-1); i++) for(k=i+1; k<n; k = k+1) (n-1) + (n-2) + … 2 + 1 = [n(n-1)]/2 = Θ(n 2 ) printf("A"); -----------------------------------------------// Example I. (similar to insertion sort processing) T(n) = …. for (i = 1; i<n; i++) for(k=i-1; k>=0; k = k-1) 1 + 2 + … + (n-1) + (n-2) = [n(n-1)]/2 = Θ(n 2 ) printf("A"); 30

Function Call Inside Loop If foo(i) has Θ(i), what is Θ for foo(0)? The time complexity for a function call is NOT 1, but the complexity derived from its code. Assume that foo has time complexity: Tfoo(n)= Θ(n) // Example 1. Independent loops => // T(n) = n* Θ(n) = Θ(n 2) n for (i = 1; i<=n; i++) foo(n); Θ(n), use n Table for Example 2 foo(i) Simplify to takes: i 1 Θ(1) 1 2 Θ(2) 2 … … … // Example 2. Dependent loops. MUST use table method: // => T(n) = Θ(n) + Θ(n-1) +…+ Θ(2)+ Θ(1) = Θ(n 2) for (i = 1; i<=n; i++) foo(i); // --> Θ(i) i Θ(i) I … … … n-1 Θ (n-1) Steps (for example 2): - Table - Summation (based on table) - Closed form - Dominant term: - Θ (Theta): Θ(n 2) n Θ (n) Θ (n 2) n-1 N 31

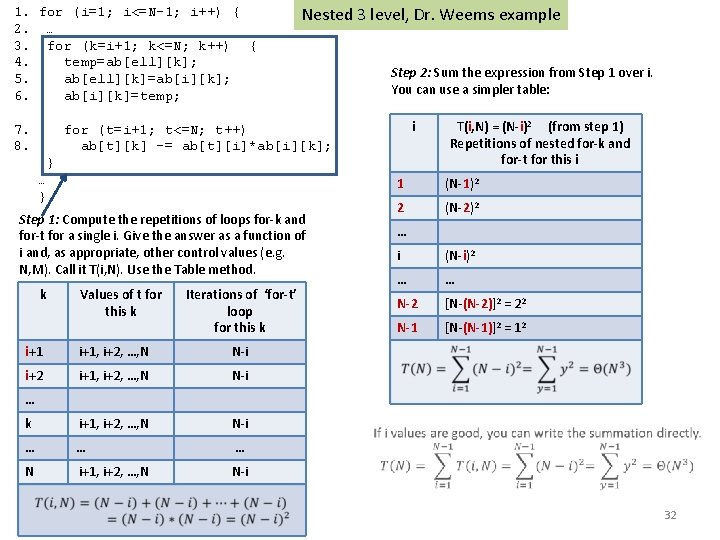
1. for (i=1; i<=N-1; i++) { 2. … 3. for (k=i+1; k<=N; k++) { 4. temp=ab[ell][k]; 5. ab[ell][k]=ab[i][k]; 6. ab[i][k]=temp; 7. 8. Nested 3 level, Dr. Weems example Step 2: Sum the expression from Step 1 over i. You can use a simpler table: i for (t=i+1; t<=N; t++) ab[t][k] -= ab[t][i]*ab[i][k]; } … } Step 1: Compute the repetitions of loops for-k and for-t for a single i. Give the answer as a function of i and, as appropriate, other control values (e. g. N, M). Call it T(i, N). Use the Table method. k Values of t for this k Iterations of ‘for-t’ loop for this k i+1, i+2, …, N N-i i+2 i+1, i+2, …, N N-i k i+1, i+2, …, N N-i … … … N i+1, i+2, …, N N-i T(i, N) = (N-i)2 (from step 1) Repetitions of nested for-k and for-t for this i 1 (N-1)2 2 (N-2)2 … i (N-i)2 … … N-2 [N-(N-2)]2 = 22 N-1 [N-(N-1)]2 = 12 … 32

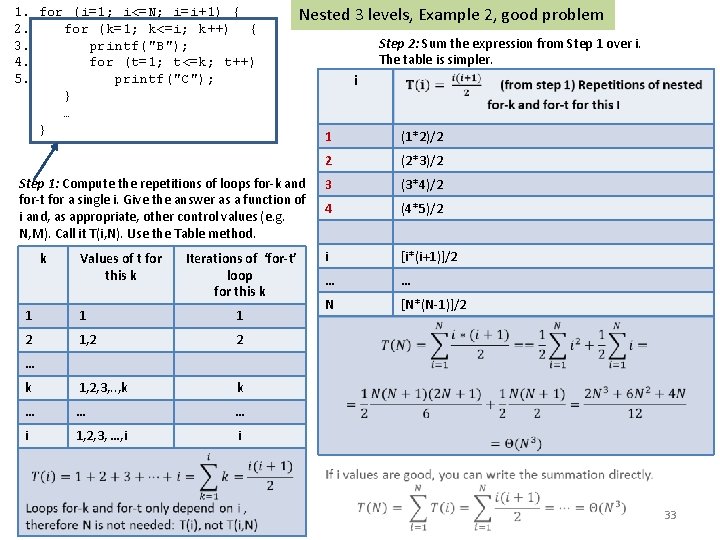
1. for (i=1; i<=N; i=i+1) { 2. for (k=1; k<=i; k++) { 3. printf("B"); 4. for (t=1; t<=k; t++) 5. printf("C"); } … } Nested 3 levels, Example 2, good problem Step 1: Compute the repetitions of loops for-k and for-t for a single i. Give the answer as a function of i and, as appropriate, other control values (e. g. N, M). Call it T(i, N). Use the Table method. k Values of t for this k Iterations of ‘for-t’ loop for this k 1 1 1 2 1, 2 2 k 1, 2, 3, . . , k k … … … i 1, 2, 3, …, i i Step 2: Sum the expression from Step 1 over i. The table is simpler. i 1 (1*2)/2 2 (2*3)/2 3 (3*4)/2 4 (4*5)/2 i [i*(i+1)]/2 … … N [N*(N-1)]/2 … 33

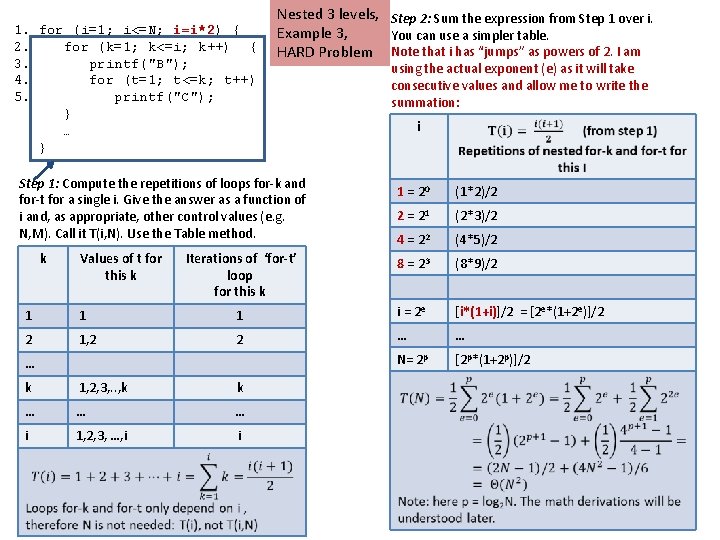
1. for (i=1; i<=N; i=i*2) { 2. for (k=1; k<=i; k++) { 3. printf("B"); 4. for (t=1; t<=k; t++) 5. printf("C"); } … } Nested 3 levels, Step 2: Sum the expression from Step 1 over i. Example 3, You can use a simpler table. HARD Problem Note that i has “jumps” as powers of 2. I am Step 1: Compute the repetitions of loops for-k and for-t for a single i. Give the answer as a function of i and, as appropriate, other control values (e. g. N, M). Call it T(i, N). Use the Table method. k Values of t for this k using the actual exponent (e) as it will take consecutive values and allow me to write the summation: i 1 = 20 (1*2)/2 2 = 21 (2*3)/2 4 = 22 (4*5)/2 Iterations of ‘for-t’ loop for this k 8 = 23 (8*9)/2 1 1 1 i = 2 e [i*(1+i)]/2 = [2 e*(1+2 e)]/2 2 1, 2 2 … … N= 2 p [2 p*(1+2 p)]/2 … k 1, 2, 3, . . , k k … … … i 1, 2, 3, …, i i 34

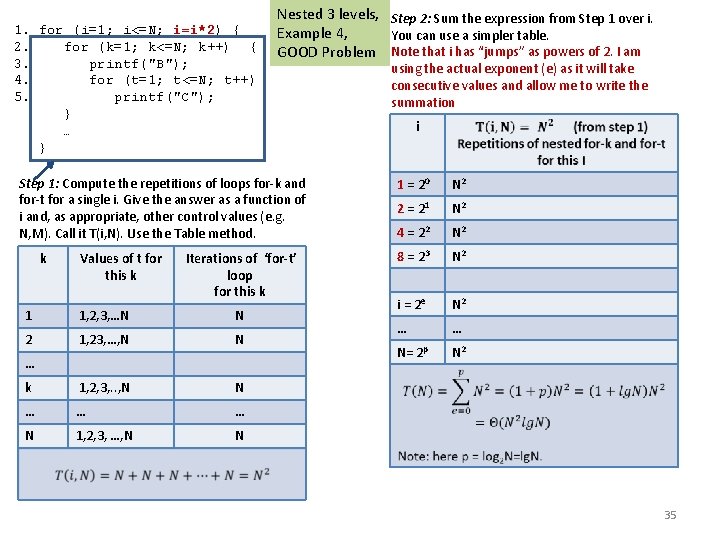
1. for (i=1; i<=N; i=i*2) { 2. for (k=1; k<=N; k++) { 3. printf("B"); 4. for (t=1; t<=N; t++) 5. printf("C"); } … } Nested 3 levels, Step 2: Sum the expression from Step 1 over i. Example 4, You can use a simpler table. GOOD Problem Note that i has “jumps” as powers of 2. I am Step 1: Compute the repetitions of loops for-k and for-t for a single i. Give the answer as a function of i and, as appropriate, other control values (e. g. N, M). Call it T(i, N). Use the Table method. k Values of t for this k Iterations of ‘for-t’ loop for this k 1 1, 2, 3, …N N 2 1, 23, …, N N k 1, 2, 3, . . , N N … … … N 1, 2, 3, …, N N … using the actual exponent (e) as it will take consecutive values and allow me to write the summation i 1 = 20 N 2 2 = 21 N 2 4 = 22 N 2 8 = 23 N 2 i = 2 e N 2 … … N= 2 p N 2 35

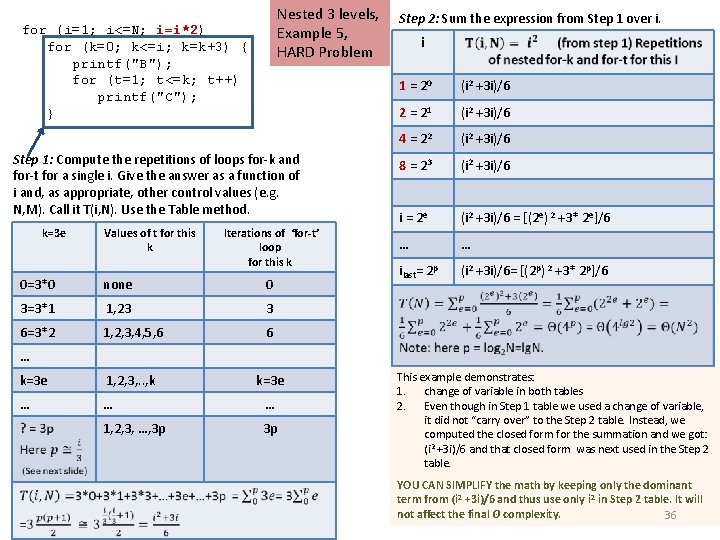
Nested 3 levels, Example 5, HARD Problem for (i=1; i<=N; i=i*2) for (k=0; k<=i; k=k+3) { printf("B"); for (t=1; t<=k; t++) printf("C"); } Step 1: Compute the repetitions of loops for-k and for-t for a single i. Give the answer as a function of i and, as appropriate, other control values (e. g. N, M). Call it T(i, N). Use the Table method. k=3 e Values of t for this k Iterations of ‘for-t’ loop for this k 0=3*0 none 0 3=3*1 1, 23 3 6=3*2 1, 2, 3, 4, 5, 6 6 k=3 e 1, 2, 3, . . , k k=3 e … … … 1, 2, 3, …, 3 p 3 p Step 2: Sum the expression from Step 1 over i. i 1 = 20 (i 2 +3 i)/6 2 = 21 (i 2 +3 i)/6 4 = 22 (i 2 +3 i)/6 8 = 23 (i 2 +3 i)/6 i = 2 e (i 2 +3 i)/6 = [(2 e) 2 +3* 2 e]/6 … … ilast= 2 p (i 2 +3 i)/6= [(2 p) 2 +3* 2 p]/6 … This example demonstrates: 1. change of variable in both tables 2. Even though in Step 1 table we used a change of variable, it did not “carry over” to the Step 2 table. Instead, we computed the closed form for the summation and we got: (i 2 +3 i)/6 and that closed form was next used in the Step 2 table. YOU CAN SIMPLIFY the math by keeping only the dominant term from (i 2 +3 i)/6 and thus use only i 2 in Step 2 table. It will not affect the final Θ complexity. 36

Formula for values of i and exact calculation of number of loop iterations – Example 1 for (i=0; i<=N; i=i+3) printf("A"); • e i=3 e 0 0 1 3 2 6 3 9 … … e 3 e … … p 37

Formula for values of i and exact calculation of number of loop iterations – Example 2 for (i=2; i<=N; i=i+3) printf("A"); • e i=2+3 e 0 2 1 5 2 8 3 11 … … e i = 2+3 e … … p ilast <=N (ilast =2+3 p) 38

Formula for values of i and exact calculation of number of loop iterations – Example 3 for (i=1; i<=N; i=i*5) printf("A"); • e i=5 e 0 1 1 5 2 25 3 125 … … e i=5 e … … p 39

Starting a business? • Facebook: more than 2. 07 billion monthly active users (in 2017) • Assume: – If you start a business that has the potential to grow this much, and – Currently you have 30 users – You need to buy software and have 2 offers: • N 2 • 1000 N, also a bit more expensive – Switching from one software to the other later on, is undesired (disruption of service, uncertainty, increased cost …) • Which one do you choose? 40

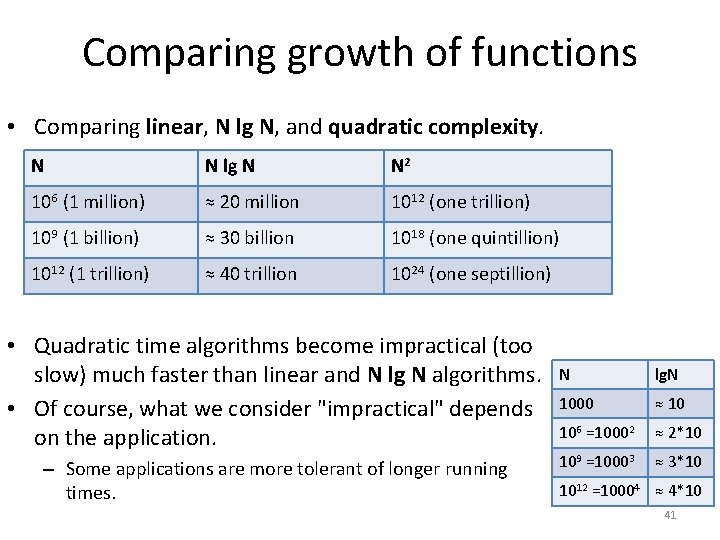
Comparing growth of functions • Comparing linear, N lg N, and quadratic complexity. N N lg N N 2 106 (1 million) ≈ 20 million 1012 (one trillion) 109 (1 billion) ≈ 30 billion 1018 (one quintillion) 1012 (1 trillion) ≈ 40 trillion 1024 (one septillion) • Quadratic time algorithms become impractical (too slow) much faster than linear and N lg N algorithms. • Of course, what we consider "impractical" depends on the application. – Some applications are more tolerant of longer running times. N lg. N 1000 ≈ 10 106 =10002 ≈ 2*10 109 =10003 ≈ 3*10 1012 =10004 ≈ 4*10 41

Θ (Theta) made simple • For any function we look at the ‘fastest growing term’ or the dominant term. – E. g. for f(n) = 15 n 3 +7 n 2+3 n+20, the dominant term is 15 n 3. – Functions of multiple variables may have more than one dominant term! Consider f(n, m) = 27 n 4 m + 6 n 3 + 7 nm 2 + 100 (Ask yourself: What if m is small and n is large? What if n is small and m is large? ) • Use Θ, Theta, for the dominant term but without the constant. – This is a oversimplification of Θ. We will study Θ formally in future lectures. • Notation: f(n) = Θ(n 2) – if the dominant term of f(n) is n 2. • Given a function, e. g. f(n) = 15 n 3 +7 n 2+3 n+20, find Theta: – find the dominant term: 15 n 3 – remove the constant: n 3 – f(n) = Θ(n 3) 42

CLRS - reference • Book reference subchapters (the first number is the chapter number): – 1. 2 Efficiency – Problem 1 -1 – See the pseudocode conventions in 2. 1 – In 2. 2 see section “Order of growth”. – 2. 1 covers Insertion sort and discusses detailed instruction count part of that. You can revisit this subchapter after we talk about insertion sort. – 2. 3 we will cover later on. (CLRS 3 rd edition) 43

Motivation for Big-Oh Notation • Given an algorithm, we want to find a function that describes the time performance of the algorithm. • Computing the number of instructions in detail is NOT desired: – It is complicated and the details are not important – The number of machine instructions and runtime depend on factors other than the algorithm: • Programming language • Compiler optimizations • Performance of the computer it runs on (CPU, memory) (There are some details that we would actually NOT want this function to include, because they can make a function unnecessarily complicated. ) • When comparing two algorithms we want to see which one is better for very large data. This is called the asymptotic behavior – It is not important what happens for small size data. – Asymptotic behavior = rate of growth = order of growth • The Big-Oh notation describes the asymptotic behavior and greatly simplifies algorithmic analysis. 44

Counting instructions: detailed Answers 1 + n* (1 + body_instr_count) false true for (init; cond; update) // assume the condition is TRUE n times body // Example A. Notice the ; at the end of the for loop. temp = 5; x = temp * 2; for (i = 0; i<n; i++) ; 2 + 1 + n* (1 + 0) = 4 + 2 n -----------------------------------------------// Example B (source: Dr. Bob Weems) - NOT REQUIRED for (i=0; i<n; i++) 1 + n * (1 + ___ ) = 2 + n * (2 + 5*p + 3*p*r) = 2 + 4*n + 5*n*p + 3*n*p*r for (t=0; t<p; t++) 1 + p* (1 + 1 + ____) = 2 + p * (3 + 2 + 3*r) = 2 + 5*p + 3*p*r { c[i][t]=0; 1 + r* (1 + 1) = 2 + 3 * r for (k=0; k<r; k++) c[i][t]+=a[i][k]*b[k][t]; 45 }

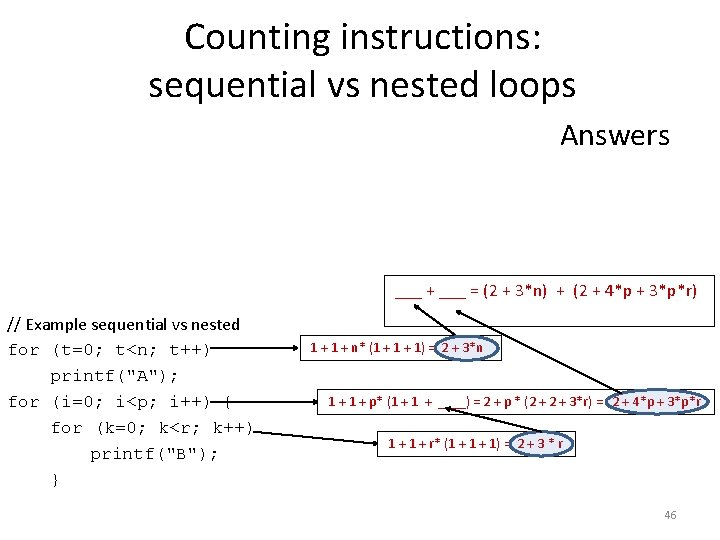
Counting instructions: sequential vs nested loops Answers ___ + ___ = (2 + 3*n) + (2 + 4*p + 3*p*r) // Example sequential vs nested for (t=0; t<n; t++) printf("A"); for (i=0; i<p; i++) { for (k=0; k<r; k++) printf("B"); } 1 + n* (1 + 1) = 2 + 3*n 1 + p* (1 + ____) = 2 + p * (2 + 3*r) = 2 + 4*p + 3*p*r 1 + r* (1 + 1) = 2 + 3 * r 46

Self study Estimate runtime • Problem: The total number of instructions in a program (or a piece of code) is 1012 and it runs on a computer that executes 109 instructions per second. How long will it take to run this program? Give the answer in seconds. If it is very large, transform it in larger units (hours, days, years). • Summary: – Total instructions: 1012 – Speed: 109 instructions/second • Answer: – Time = (total instructions)/speed = (1012 instructions) / (109 instr/sec) = 103 seconds ~ 15 minutes • Note that this computation is similar to computing the time it takes to travel a certain distance ( e. g. 120 miles) given the speed (e. g. 60 miles/hour). 47

Self study Estimate runtime • A slightly different way to formulate the same problem: – total number of instructions in a program (or a piece of code) is 1012 and – it runs on a computer that executes one instruction in one nanosecond (10 -9 seconds) – How long will it take to run this program? Give the answer in seconds. If it is very large, transform it in larger units (hours, days, years) • Summary: – 1012 total instructions – 10 -9 seconds per instruction • Answer: – Time = (total instructions) * (seconds per instruction) = (1012 instructions)* (10 -9 sec/instr) = 103 seconds ~ 15 minutes 48

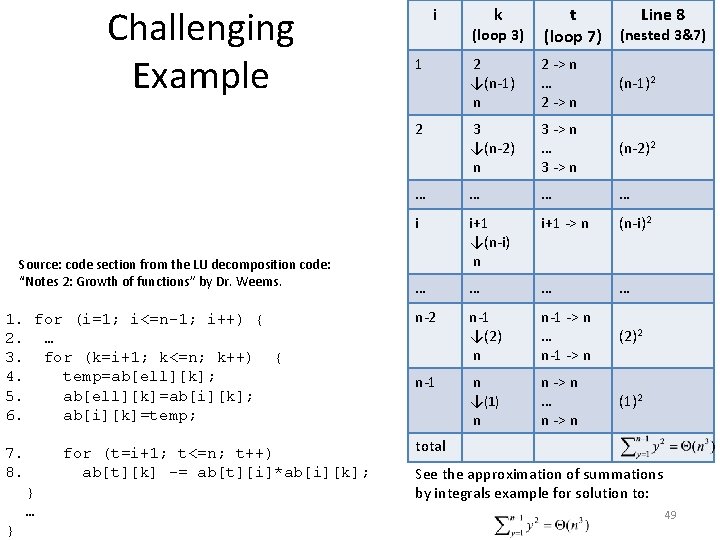
Challenging Example Source: code section from the LU decomposition code: “Notes 2: Growth of functions” by Dr. Weems. 1. for (i=1; i<=n-1; i++) { 2. … 3. for (k=i+1; k<=n; k++) { 4. temp=ab[ell][k]; 5. ab[ell][k]=ab[i][k]; 6. ab[i][k]=temp; 7. 8. for (t=i+1; t<=n; t++) ab[t][k] -= ab[t][i]*ab[i][k]; } … } i k (loop 3) t (loop 7) Line 8 1 2 ↓(n-1) n 2 -> n … 2 -> n (n-1)2 2 3 ↓(n-2) n 3 -> n … 3 -> n (n-2)2 … … i i+1 ↓(n-i) n i+1 -> n (n-i)2 … … n-2 n-1 ↓(2) n n-1 -> n … n-1 -> n (2)2 n-1 n ↓(1) n n -> n … n -> n (1)2 (nested 3&7) total See the approximation of summations by integrals example for solution to: 49