Time and Frequency Characterization of Signals Systems Frequency

Time and Frequency Characterization of Signals & Systems • Frequency Domain Characterization through multiplication of Fourier Transform of input signal and system frequency response. ( Transfer Function). • Time Domain Characterization through convolution of input signal and system impulse response. Convenient to use frequency domain because easy operation of Multiplication as oppose to operation of convolution in time domain. 1

Magnitude and Phase Representation of Fourier Transforms 2

Magnitude-Phase Representation of The Frequency Response of LTI Systems x(t) X(jw) h(t) H(jw) y(t)=h(t)*x(t) Y(jw)=H(jw)X(jw) |Y(jw)| = |H(jw)| |X(jw)| x[n] y[n]=x[n]*h[n] 3

Linear Phase and Group Delay of LTI Systems x(t) X(jw) h(t) H(jw) y(t)=h(t)*x(t) Y(jw)=H(jw)X(jw) |Y(jw)| = |H(jw)| |X(jw)| 4

Log-Magnitude and Bode plots The absolute values of the magnitude of the transfer function of a system are normally converted into decibels define as 5

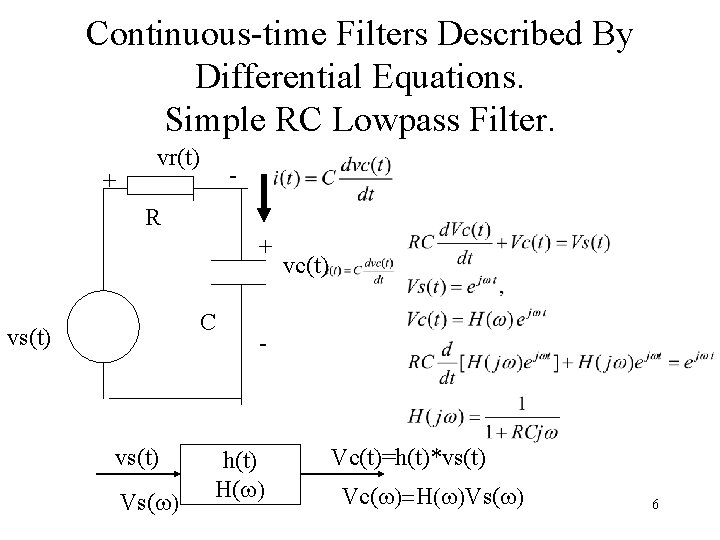
Continuous-time Filters Described By Differential Equations. Simple RC Lowpass Filter. + vr(t) - R + C vs(t) Vs(w) vc(t) - h(t) H(w) Vc(t)=h(t)*vs(t) Vc(w)=H(w)Vs(w) 6

Continuous-time Filters Described By Differential Equations. Simple RC Lowpass Filter. + vr(t) - R + vc(t) vs(t) C - 7

First-order Recursive Discretetime Filter 8

x[n] First-order Recursive Discretetime Filter y[n] + ay[n-1] D a y[n-1] h[n] x[n] X(w) H(w) y[n]=x[n]*h[n] Y(w)=X(w)H(w) 9

First-order Recursive Discretetime Filter 10

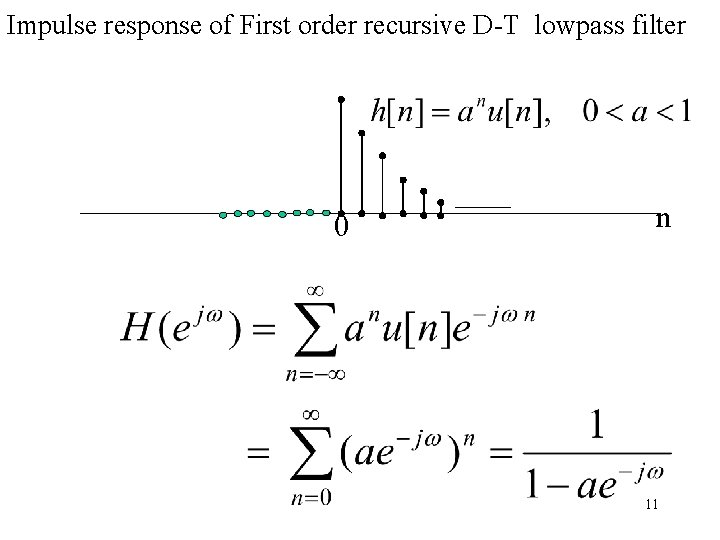
Impulse response of First order recursive D-T lowpass filter 0 n 11

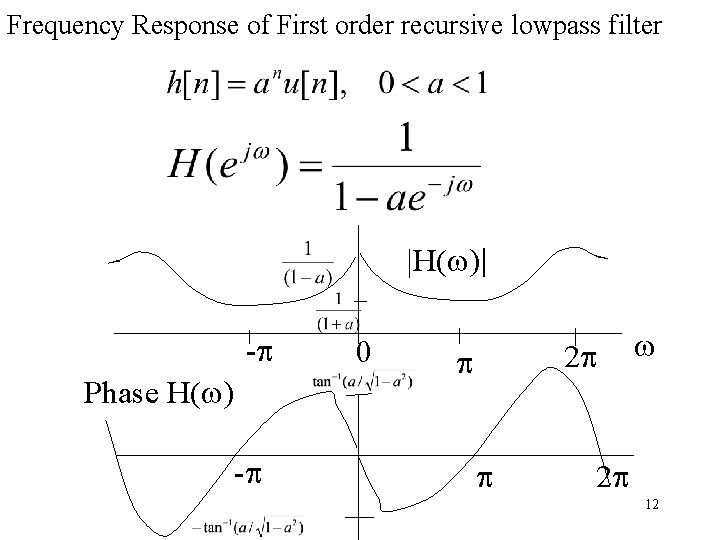
Frequency Response of First order recursive lowpass filter |H(w)| -p Phase H(w) -p 0 2 p p p w 2 p 12

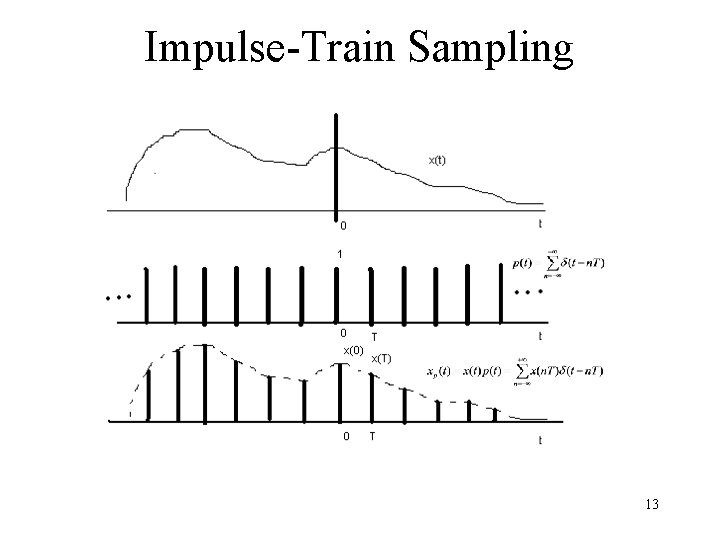
Impulse-Train Sampling 13

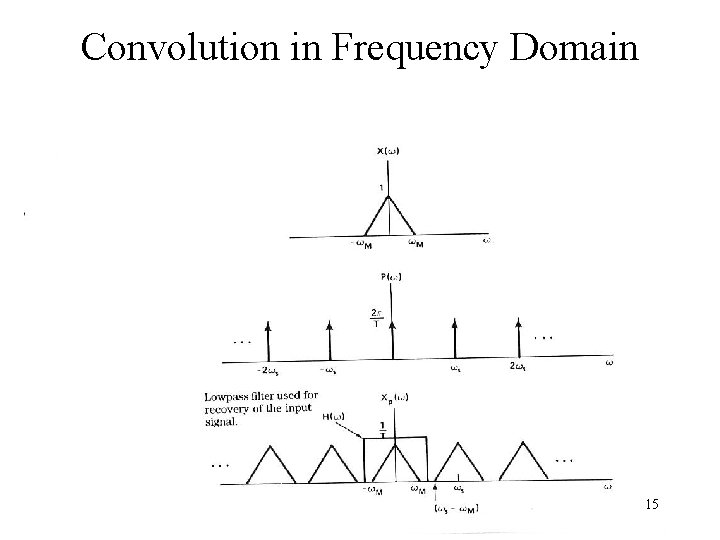
Multiplication/Modulation Property p(t) P(w) X x(t) X(w) 14

Convolution in Frequency Domain 15

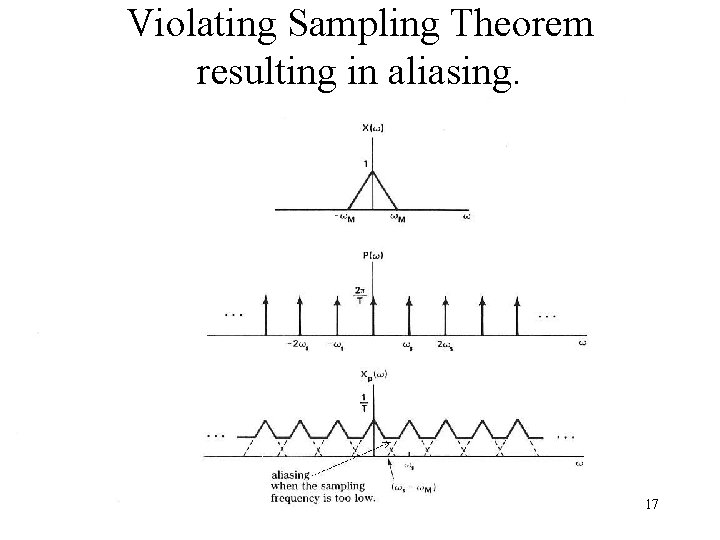
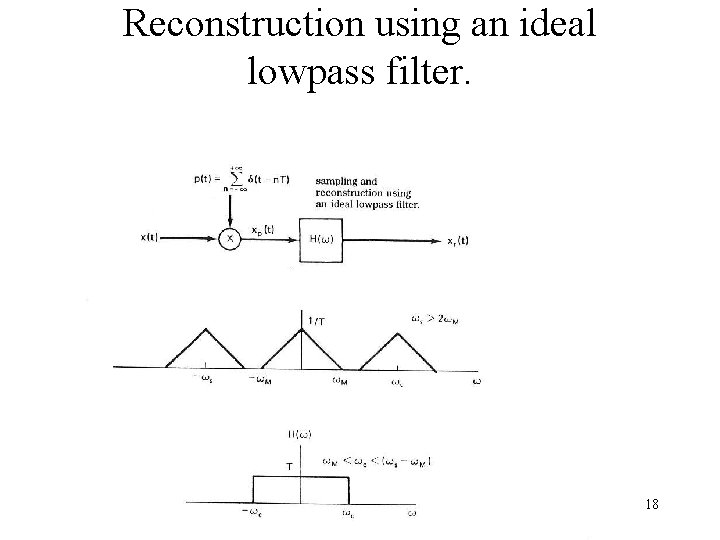
Sampling Theorem 16

Violating Sampling Theorem resulting in aliasing. 17

Reconstruction using an ideal lowpass filter. 18

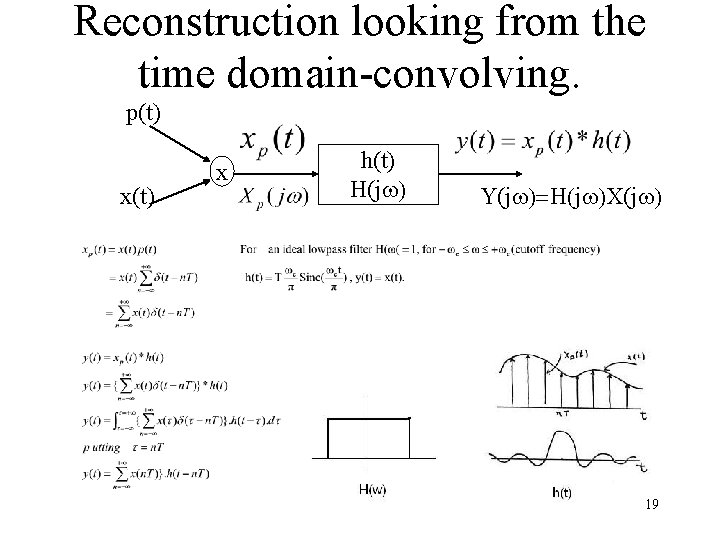
Reconstruction looking from the time domain-convolving. p(t) x h(t) H(jw) Y(jw)=H(jw)X(jw) 19

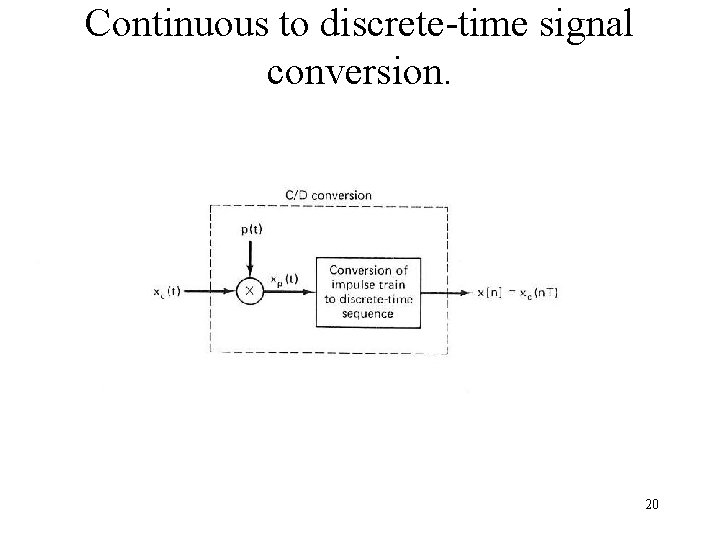
Continuous to discrete-time signal conversion. 20

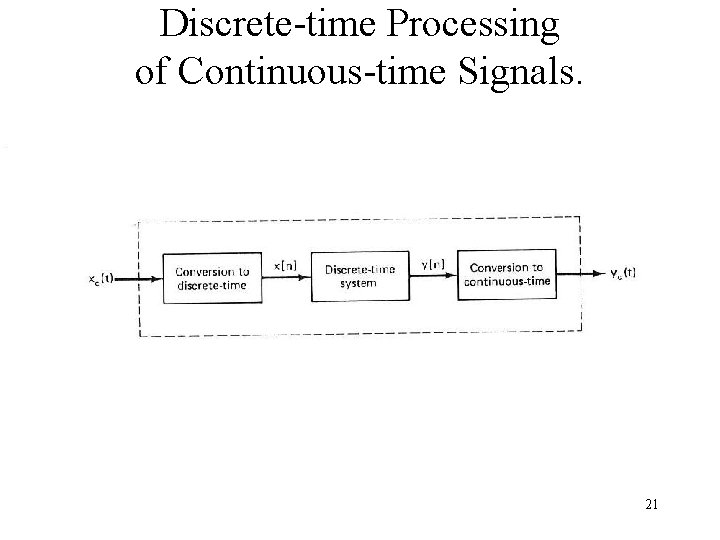
Discrete-time Processing of Continuous-time Signals. 21

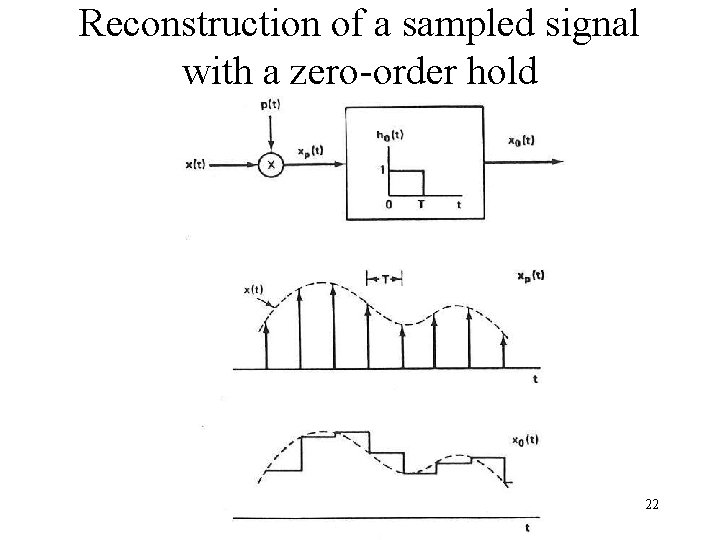
Reconstruction of a sampled signal with a zero-order hold 22

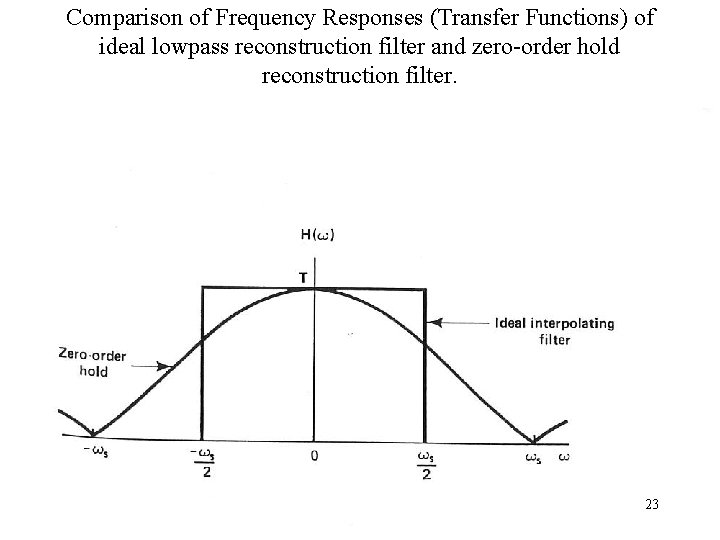
Comparison of Frequency Responses (Transfer Functions) of ideal lowpass reconstruction filter and zero-order hold reconstruction filter. 23

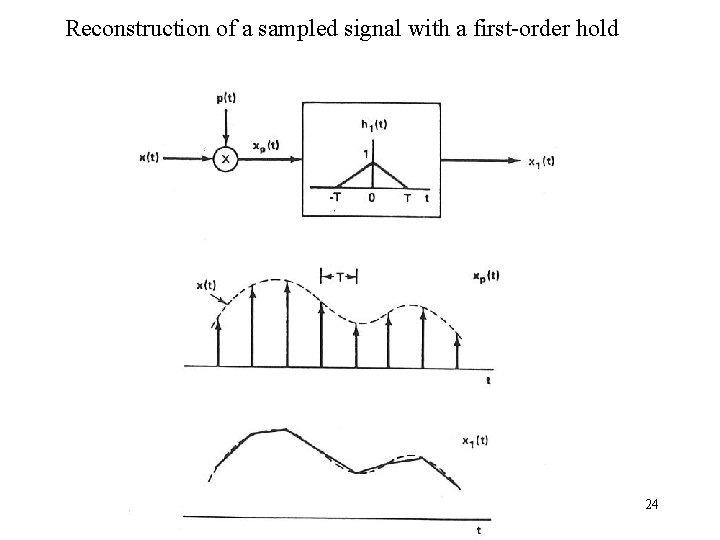
Reconstruction of a sampled signal with a first-order hold 24

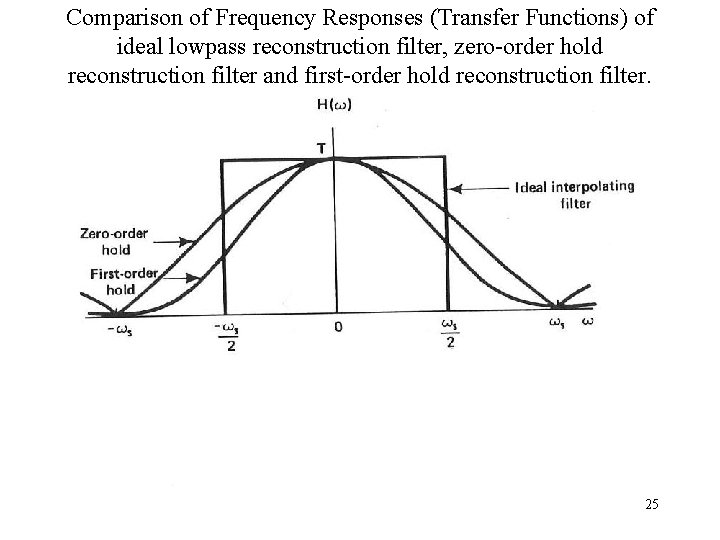
Comparison of Frequency Responses (Transfer Functions) of ideal lowpass reconstruction filter, zero-order hold reconstruction filter and first-order hold reconstruction filter. 25

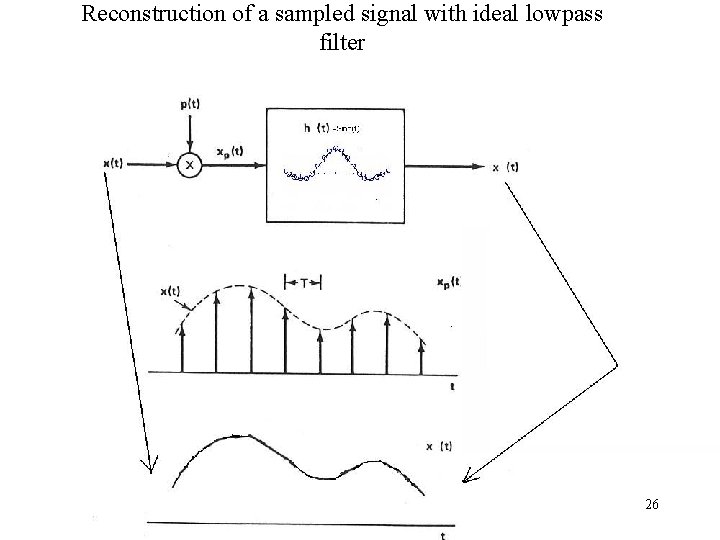
Reconstruction of a sampled signal with ideal lowpass filter 26