Tiled Polygon Traversal Using HalfPlane Edge Functions Joel

Tiled Polygon Traversal Using Half-Plane Edge Functions Joel Mc. Cormack & Bob Mc. Namara www. compaq. com

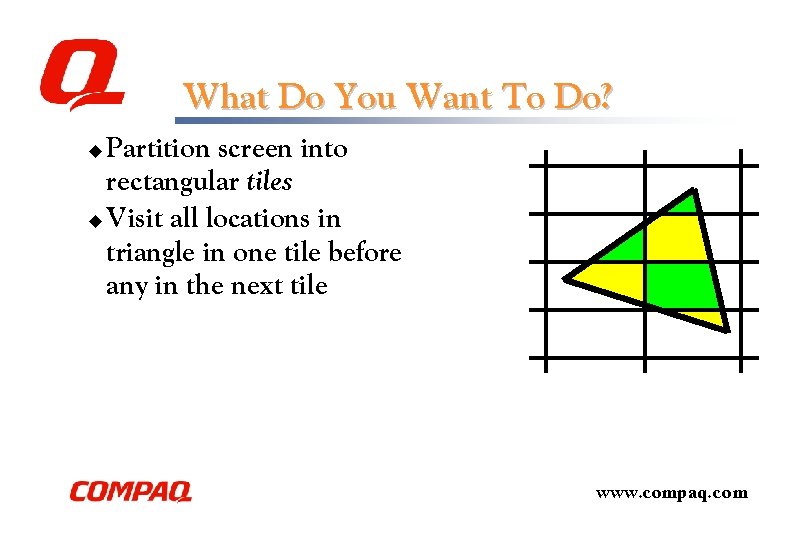
What Do You Want To Do? Partition screen into rectangular tiles u Visit all locations in triangle in one tile before any in the next tile u www. compaq. com

Why Do You Want To Do That? u Improve frame buffer memory access patterns DRAM access to open page faster than non-open page l Staying on open page improves average access time. . . l …and improves prefetching of pages into other banks l u Improve texture cache access patterns l Staying within limited area increases cache hits by exploiting 2 D spatial coherency of texel accesses www. compaq. com

Outline Half-Plane Edge Functions u Fragment Stamp and Movement u A Simple Traversal Algorithm u A Tiling Traversal Algoriththm u Uses of Tiling and Even Metatiling u Conclusions u www. compaq. com

Half-Plane Edge Functions Many rasterizers traverse polygons by surrounding them with edge functions going from vertex to vertex u E 01(x, y) = (x – x 0)(y 1 – y 0) – (y – y 0)(x 1 – x 0) splits 2 D plane into two halves: u Non-negative on or to right of edge l Negative to left of edge l u If all edge functions at (x, y) have same sign, then (x, y) is within polygon www. compaq. com

Triangle Surrounded By Edge Functions Non-negative half-planes have “shadow” lines u All three edges non-negative in shaded yellow area u www. compaq. com

Zen and the Art of Polygon Traversal u Scanline traversal like being in the military: Start exactly right here l Go exactly to there, then stop l Repeat l u Half-plane traversal more like Zen wandering to enlightenment: Where am I? l Where can I go? Have I reached my limits? l Okay, how about that away? (For now. ) l www. compaq. com

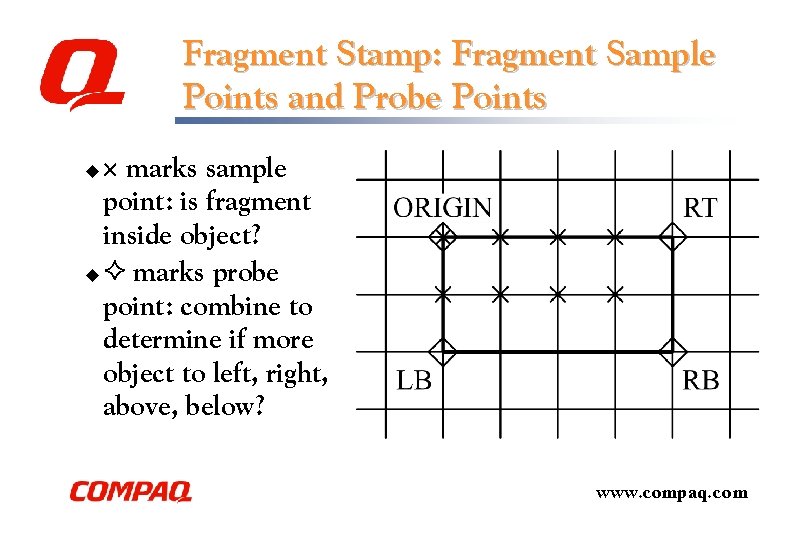
Fragment Stamp: Fragment Sample Points and Probe Points marks sample point: is fragment inside object? u marks probe point: combine to determine if more object to left, right, above, below? u www. compaq. com

Fragment Stamp: Which Adjacent Stamp Positions Are Valid? Does a stamp segment, e. g. (RB, LB), intersect the object (and thus indicate valid adjacent position)? u Probably, if: u Each edge contains at least one stamp segment endpoint l Object’s bounding box contains at least one stamp segment endpoint l www. compaq. com

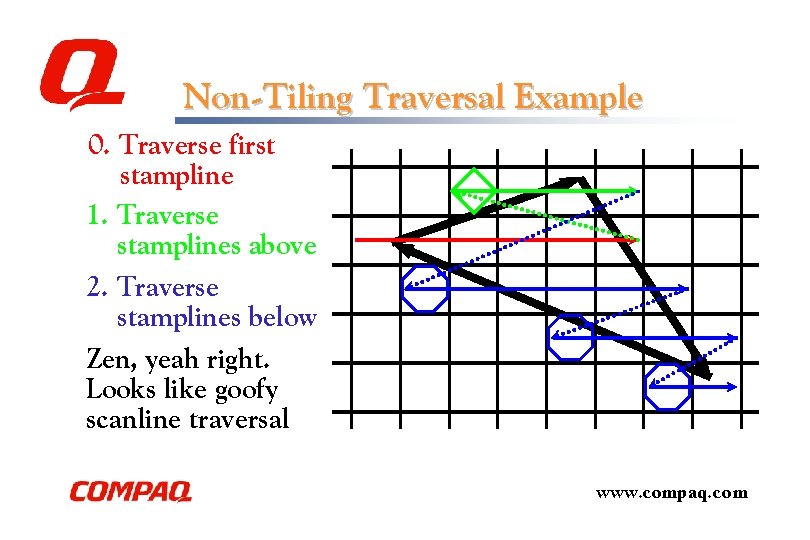
Non-Tiling Traversal Example 0. Traverse first stampline 1. Traverse stamplines above 2. Traverse stamplines below Zen, yeah right. Looks like goofy scanline traversal www. compaq. com

A Non-Tiling Traversal Algorithm Starting at leftmost vertex. . . 0. Proceed right as long as valid position Save first valid up position l Save first valid down position l 1. Jump to saved up, proceed right as long as valid l Save first valid up, repeat 1 until no more up 2. Jump to saved down, proceed right as long as valid l Save first valid down, repeat 2 until no more down www. compaq. com

Tiling Traversal Observations u Easy to obey top and bottom tile boundaries Go down from initial scanline until hit tile bottom l Then do original algorithm starting at Step 1 (go up) l u Need new saved state to obey right tile boundary Original algorithm, but stop at right tile boundary, and save first right position in next tile over l Traverse all of object in first tile column l Then move to saved right position and restart algorithm l u Combine both to obey all tile boundaries www. compaq. com

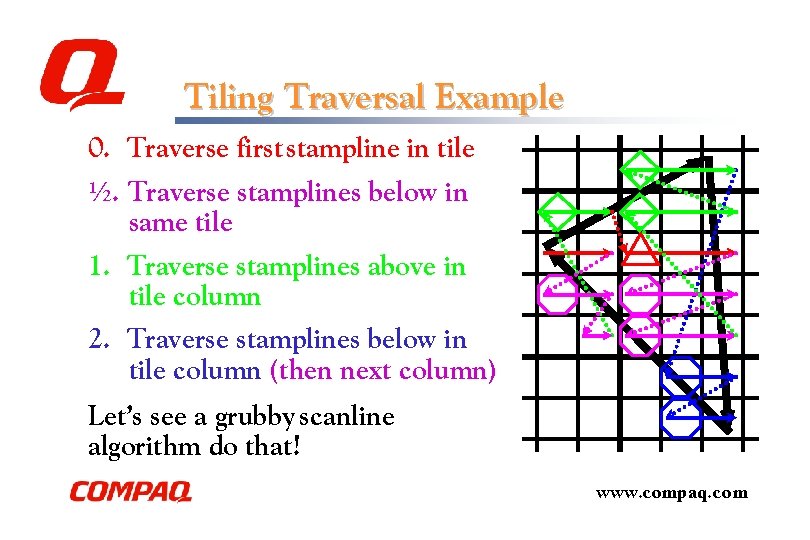
Tiling Traversal Example 0. Traverse first stampline in tile ½. Traverse stamplines below in same tile 1. Traverse stamplines above in tile column 2. Traverse stamplines below in tile column (then next column) Let’s see a grubby scanline algorithm do that! www. compaq. com

A Tiling Traversal Algorithm 0. Proceed right as long as valid position and in same tile l Save first valid up and down positions ½. Jump to saved down, proceed right in same tile l Save first valid down, repeat ½ while down in same tile 1. Jump to saved up, proceed right in same tile l Save first valid up, repeat 1 until no more up 2. Jump to saved down, proceed right in same tile l Save first valid down, repeat 2 until no more down 3. Jump to saved right (in new tile), go back to Step 0 www. compaq. com

Obvious Uses for Tiling u Optimize frame buffer access patterns Tile size & dimensions match 2 D page in frame buffer l All positions in object & page visited before new page l Increases available time to prefetch next page l Serpentine variation reduces non-prefetchable crossings l u Reduce texture cache miss rate Tile size related to texture cache size l Tile dimensions long and skinny to minimize texture fetches that will suffer capacity misses l www. compaq. com

Subset Metatiling Visit all location in tile before next tile, and all tiles in metatile before next metatile u Requires three additional save states, though u www. compaq. com

Subset Metatiling Uses u Optimize hierarchical frame buffer caching l Mitsubishi 3 D-RAM has two cache levels Optimize hierarchical texture caches u Or optimize frame buffer access and texture cache access simultaneously u www. compaq. com

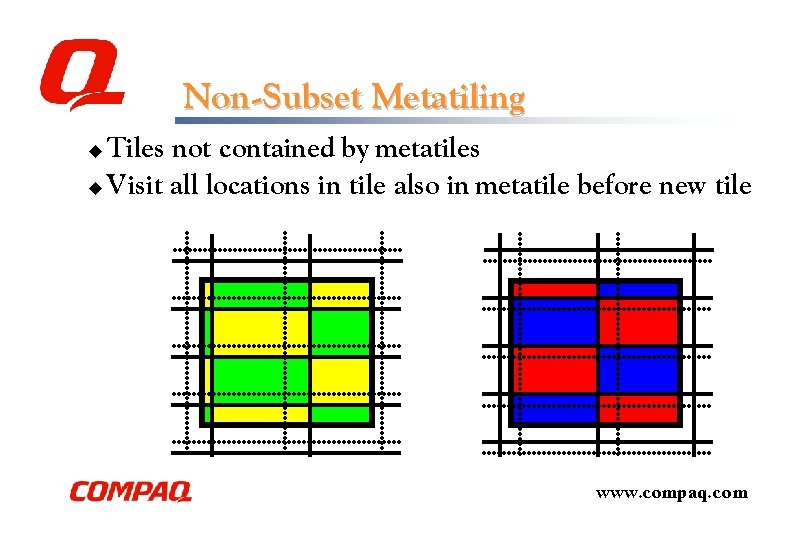
Non-Subset Metatiling Tiles not contained by metatiles u Visit all locations in tile also in metatile before new tile u www. compaq. com

Conclusions Tiling is easy to add to a half-plane based rasterizer u Tiling increases frame buffer memory efficiency u Tiling increases effectiveness of texture cache u Scanline rasterizers should die a quiet death u www. compaq. com