Tight Bounds for Parallel Randomized Load Balancing Christoph

Tight Bounds for Parallel Randomized Load Balancing Christoph Lenzen and Roger Wattenhofer Christoph Lenzen, STOC 2011

What is Load Balancing? optimizing storage utilization work sharing hashing low-congestion routing Christoph Lenzen, STOC 2011
An Example of Parallel Load Balancing • • fully connected network small & equal bandwidths (one message/round) n nodes need to send/receive up to n messages minimize number of rounds Christoph Lenzen, STOC 2011
An Example of Parallel Load Balancing • • fully connected network small & equal bandwidths (one message/round) n nodes need to send/receive up to n messages minimize number of rounds Christoph Lenzen, STOC 2011
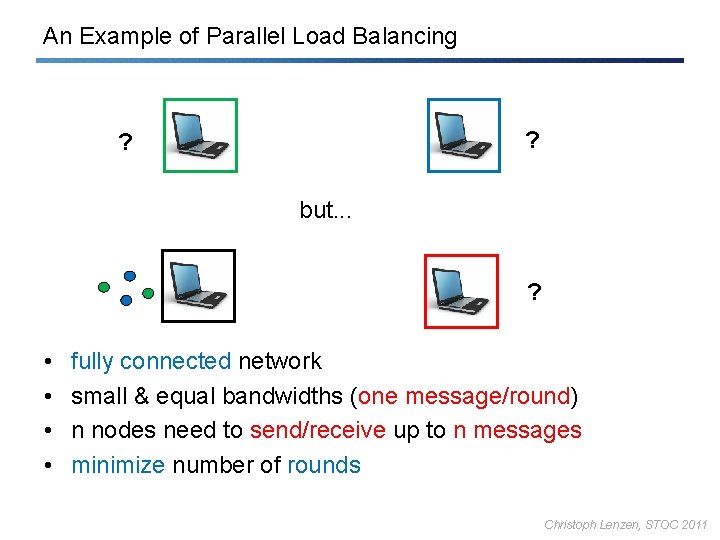
An Example of Parallel Load Balancing ? ? but. . . ? • • fully connected network small & equal bandwidths (one message/round) n nodes need to send/receive up to n messages minimize number of rounds Christoph Lenzen, STOC 2011
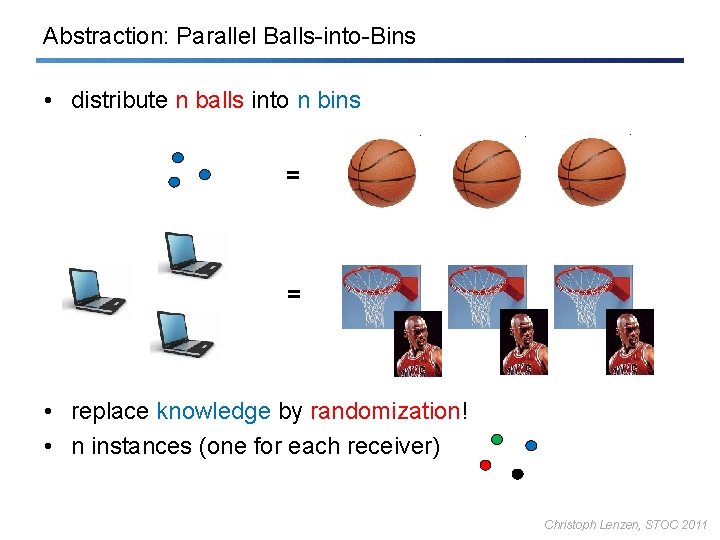
Abstraction: Parallel Balls-into-Bins • distribute n balls into n bins = = • replace knowledge by randomization! • n instances (one for each receiver) Christoph Lenzen, STOC 2011

Naive Approach: Fire-and-Forget • throw balls uniformly independently at random (u. i. r. ) • max. load with high probability (w. h. p. ) Christoph Lenzen, STOC 2011
The Power of Two Choices (e. g. Azar et al. , SIAM J. of Comp. ‘ 99) • • • inspect two bins and decide take least loaded max. load w. h. p. d choices: w. h. p. possible Vöcking, JACM‘ 92. . . but not parallel! Christoph Lenzen, STOC 2011

The Parallel Power of Two Choices • strongest upper bound: Stemann, SPAA‘ 96 max. load • tight for constant r in r rounds Adler et al. , STOC‘ 95 • . . . and certain algorithms: – non-adaptive (fix bins to contact in advance) – symmetric (all choices uniform) Christoph Lenzen, STOC 2011
An Adaptive Algorithm • • ≈ • < • contact one bin every bin accepts one ball n/e balls remain (w. h. p. ) contact 2<e bins n/e 2 balls remain (w. h. p. ) contact k<e 2 bins, and so on Christoph Lenzen, STOC 2011

The Power of the Tower • • • termination in rounds cap # contacted bins at total messages w. h. p. in exp. (for each ball and bin) can enforce max. load 2 tolerates message loss & faulty bins log* x x 0 1 1 2 2 4 3 16 4 65, 536 5 ≈1020, 000 Christoph Lenzen, STOC 2011
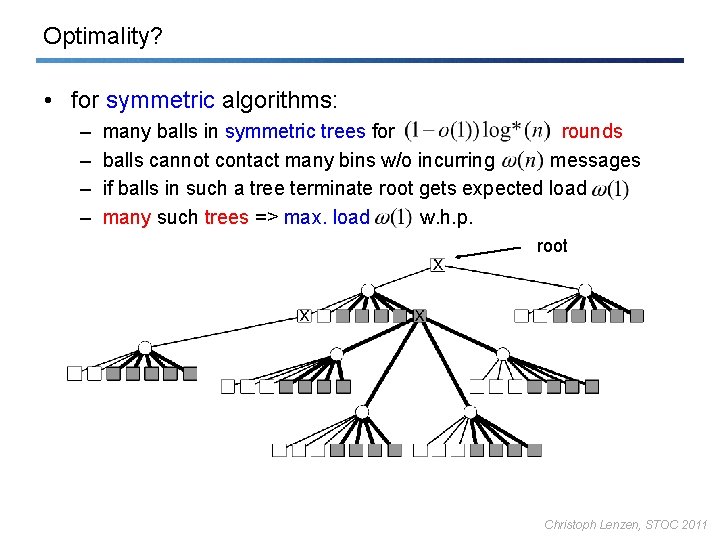
Optimality? • for symmetric algorithms: – – many balls in symmetric trees for rounds balls cannot contact many bins w/o incurring messages if balls in such a tree terminate root gets expected load many such trees => max. load w. h. p. root Christoph Lenzen, STOC 2011

No Faster Solution Possible, unless. . . • bin loads of are accepted, place s balls at once • bins have "identities" known to all balls • messages are used Christoph Lenzen, STOC 2011
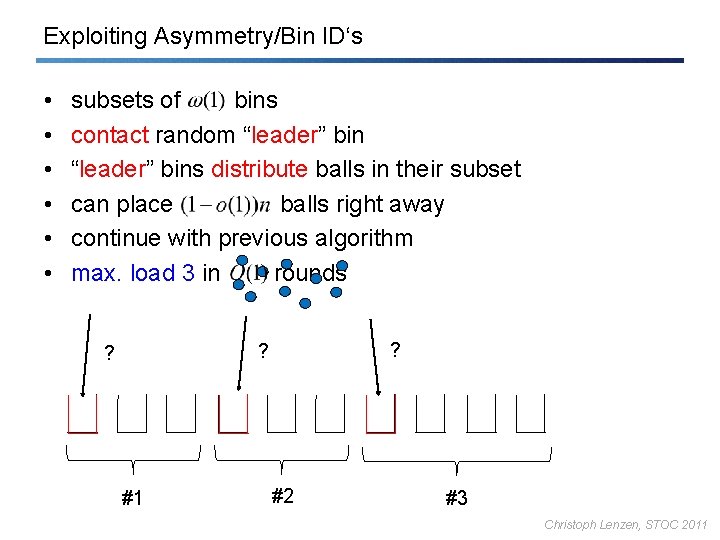
Exploiting Asymmetry/Bin ID‘s • • • subsets of bins contact random “leader” bins distribute balls in their subset can place balls right away continue with previous algorithm max. load 3 in rounds ? ? ? #1 #2 #3 Christoph Lenzen, STOC 2011
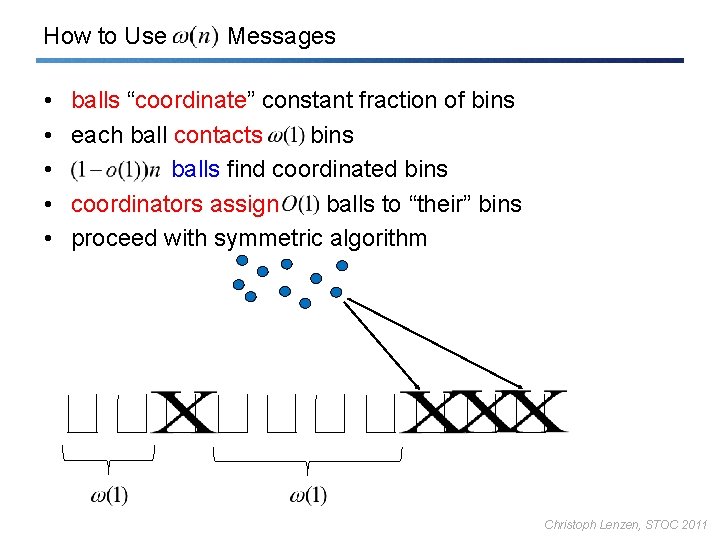
How to Use • • • Messages balls “coordinate” constant fraction of bins each ball contacts bins balls find coordinated bins coordinators assign balls to “their” bins proceed with symmetric algorithm Christoph Lenzen, STOC 2011

Summary • optimal symmetric solution – max. load 2, mess. , rounds • constant-time if: – global enumeration of bins – messages – max. load Christoph Lenzen, STOC 2011

. . . hey, What Happened to the Original Problem? ! • can be solved in • can be used to sort rounds keys in rounds Patt-Shamir and Teplitsky, PODC‘ 11 Christoph Lenzen, STOC 2011

Thank You! Questions or Comments? Christoph Lenzen, STOC 2011
- Slides: 18