Ti indicator random variable of the event that

Ti = indicator random variable of the event that i-th throw results in a tail E[T] = E[T 1] + … + E[T 6] = 6*(1/2) = 3 P(T=3) = P(H=3) = binomial(6, 3)/26 = 5/16 < 1/2

E[Xi, j] = ½ (consider only i<j) X= Xi, j 1 i<j n E[X] = n(n-1) /4

There exists c such that T(n) T(n/2)+T(n/3)+c*n. We need to show that there exists d such that T(n) d*n for all n. Induction step: T(n) T(n/2) + T(n/3) + c*n d*n/2 + d*n/3 + c*n d*n + (c-d/6)*n d*n, taking d=6 c.

l m+1

if B A[m] then

Reverse(a, b) for i from a to a+b do swap(A[i], A[a+b-i]); Rotate(k) Reverse(1, k) Reverse(k+1, n) Reverse(1, n) 1, …. , k, k+1, …. , n k, …. , 1, n, …. , k+1, …. , n, 1, …. , k

1) find the median m of A 2) m m m sum S 3) if Sgeq C then recurse on A[n/2. . n] else recurse on A[1. . n/2] with C’=C-S

T(n) = T(n/2) + O(n) 3) if Sgeq C then recurse on A[n/2. . n] else recurse on A[1. . n/2] with C’=C-S

Coupon collector problem n coupons to collect What is the expected number of cereal boxes that you need to buy?

Coupon collector problem Assume that a dart throw is uniform in the circle. Let p be The fraction occupied by the bull’s eye. Expected number of darts needed to hit the bull’s eye ?

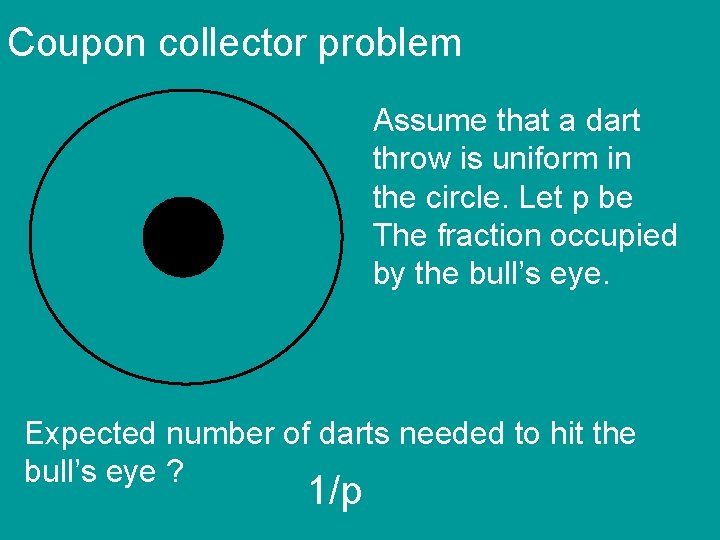
Coupon collector problem Assume that a dart throw is uniform in the circle. Let p be The fraction occupied by the bull’s eye. Expected number of darts needed to hit the bull’s eye ? 1/p

What is the expected number of boxes that I buy in k-th phase ? k-th phase = when I have k different Kinds of coupons. E[X 0] = 1 … E[Xk] = ? … E[Xn-1] = n

What is the expected number of boxes that I buy in k-th phase ? k-th phase = when I have k different Kinds of coupons. E[X 0] = 1 … E[Xk] = n/(n-k) … E[Xn-1] = n

What is the expected number of boxes that I buy in k-th phase ? k-th phase = when I have k different Kinds of coupons. n-1 X=X 0+X 1+…+Xn-1 n = n-k k=0 n 1 =n k k=1 = (n ln n)

What is the expected number of boxes that I buy in k-th phase ? k-th phase = when I have k different Kinds of coupons. n-1 = X=X 0+X 1+…+Xn-1 n = n-k k=0 E[X]=E[X 0]+…+E[Xn-1] n 1 =n k k=1 = (n ln n)

Harmonic numers n ln n 1 k k=1 1+ln n

Randomized algorithm for “median” SELECT k-th element for random x 1) <x L =x >x R 2) recurse on the appropriate part

Randomized algorithm for “median” Las Vegas algorithm (never makes error, randomness only influences running time) The identity testing algorithm was Monte Carlo algorithm with 1 sided error.

Markov inequality For non-negative random variable X: P(X > a. E[X]) < 1/a P(X a. E[X]) 1/a

Variance For a random variable X: V[ X ] = E[ (X-E[X])2 ] What is the variance of X=the number on a (6 -sided) dice ?

Variance For a random variable X: V[ X ] = E[ (X-E[X])2 ] Y = (X-E[X])2 P( Y > a. E[Y] ) < 1/a P( (X-E[X])2 > a. V[X] ) < 1/a P( (X-E[X])2 > b 2. E[X]2 ) < V[X]/(b 2 E[X]2) P( |X-E[X]| > b. E[X] ) < V[X] E[X]2 * 1 b 2

Chebychev’s inequality P( |X-E[X]| > b. E[X] ) < V[X] E[X]2 * P( (1 -b)*E[X] X (1+b)*E[X] ) >1 - V[X] E[X]2 * 1 b 2