ThreeDimensional Graphics Problem l How can you effectively

Three-Dimensional Graphics Problem l How can you effectively display 3 -D information on a 2 -D display? CS-321 Dr. Mark L. Hornick 1

Ambiguous images – which one is it? ? ? CS-321 Dr. Mark L. Hornick 2

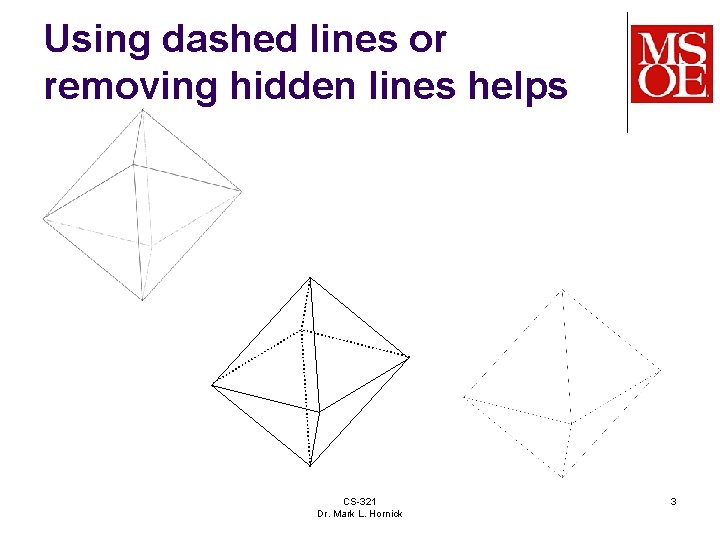
Using dashed lines or removing hidden lines helps CS-321 Dr. Mark L. Hornick 3

Stereoviews pairs CS-321 Dr. Mark L. Hornick 4

Depth Cueing CS-321 Dr. Mark L. Hornick 5

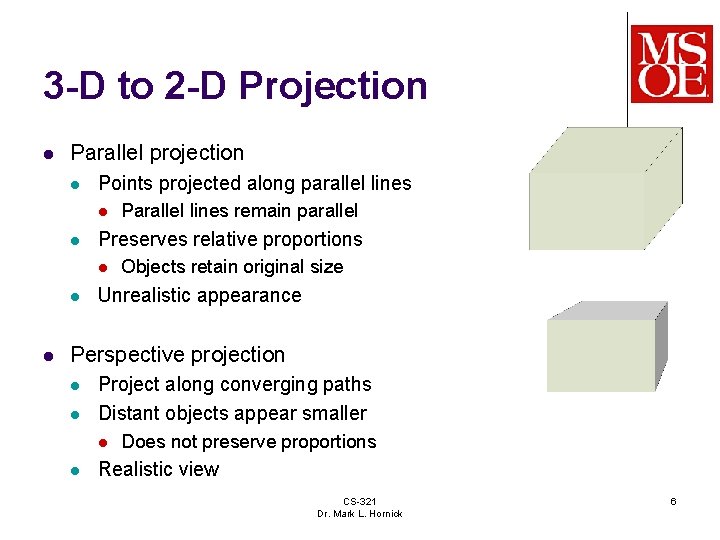
3 -D to 2 -D Projection l Parallel projection l Points projected along parallel lines l l Preserves relative proportions l l l Parallel lines remain parallel Objects retain original size Unrealistic appearance Perspective projection l l Project along converging paths Distant objects appear smaller l l Does not preserve proportions Realistic view CS-321 Dr. Mark L. Hornick 6

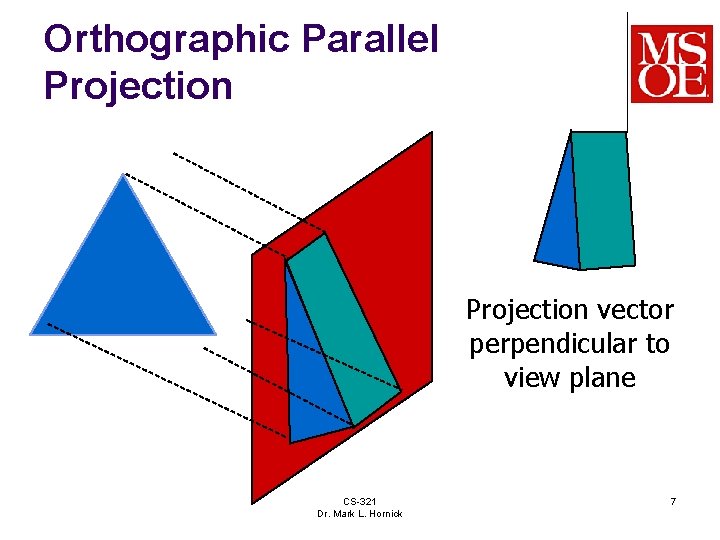
Orthographic Parallel Projection vector perpendicular to view plane CS-321 Dr. Mark L. Hornick 7

Orthographic Transform l Transform world to view coordinates l l l So direction vector aligned to +z Keep xd and yd coordinates “Flatten” zd coordinate l l l Ignore? Set to zero? Use for depth cueing? CS-321 Dr. Mark L. Hornick 8

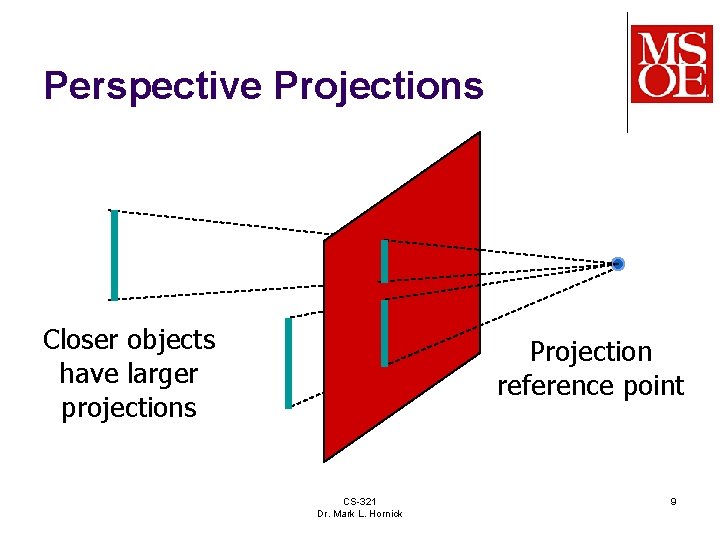
Perspective Projections Closer objects have larger projections Projection reference point CS-321 Dr. Mark L. Hornick 9

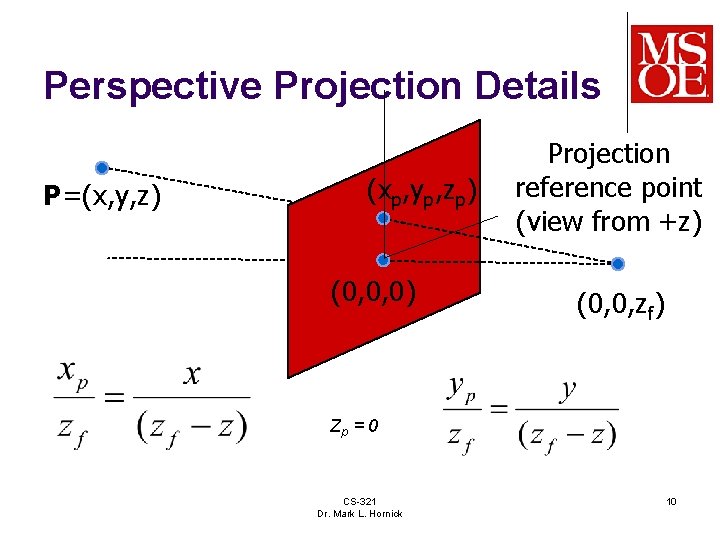
Perspective Projection Details P=(x, y, z) (xp, yp, zp) (0, 0, 0) Projection reference point (view from +z) (0, 0, zf) Zp = 0 CS-321 Dr. Mark L. Hornick 10

Perspective Projection Details Zp = 0 CS-321 Dr. Mark L. Hornick 11

Perspective Matrix CS-321 Dr. Mark L. Hornick 12

Perspective Transformation CS-321 Dr. Mark L. Hornick 13

Model Coordinates to Device Coordinates • Including scaling and perspective matrices M and S • Computes the non-normalized homogeneous transformed vector vh • The normalized homogeneous transformed vector vd: CS-321 Dr. Mark L. Hornick 14