Threedimensional figures or solids can be made up

Three-dimensional figures, or solids, can be made up of flat or curved surfaces. Faces– the polygons that make the polyhedron Edges– A line segment formed by the intersection of 2 faces. Vertices – a point where 3 or more edges meet.

In this lesson, you will learn how to visualize the 2 D cross -sections of 3 D shapes Cross Section: the 2 dimensional shape that results from cutting through the solid -
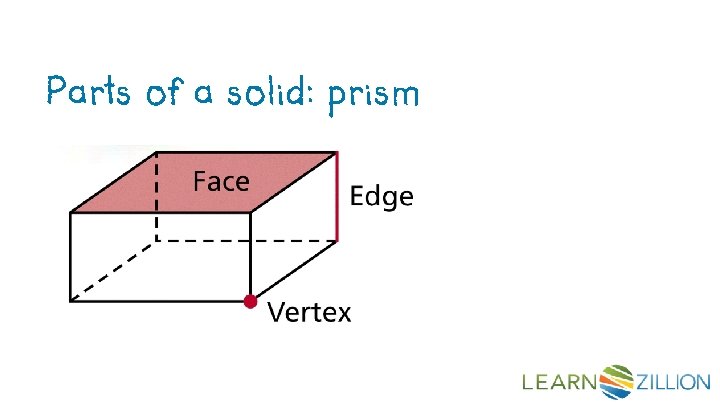
Let’s Review Parts of a solid: prism

Core Lesson Effect of slicing plane When a plane intersects the faces, the result will be the edges of a 2 D figure The cross section would be a hexagon.
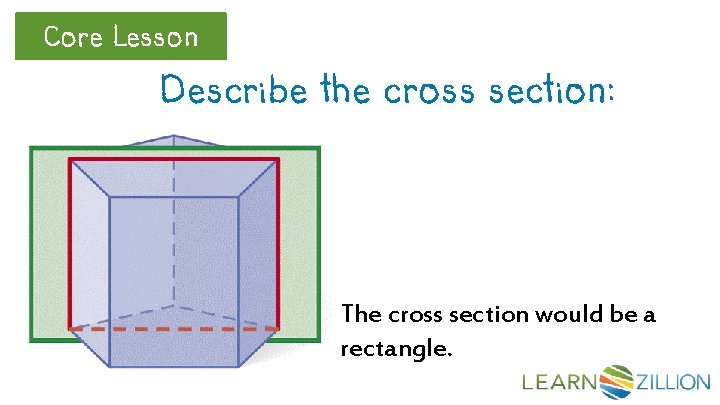
Core Lesson Describe the cross section: The cross section would be a rectangle.
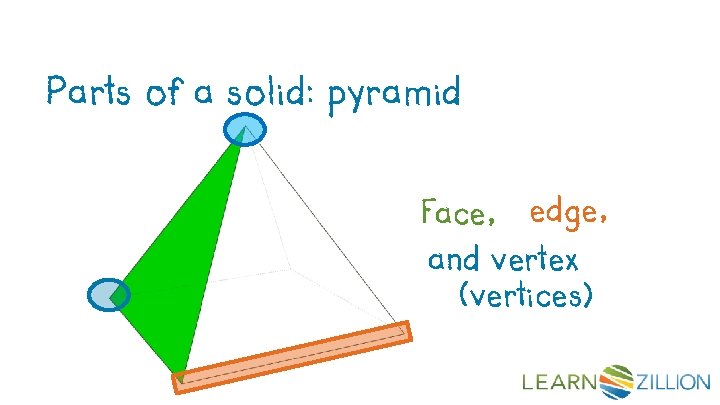
Let’s Review Parts of a solid: pyramid Face, edge, and vertex (vertices)
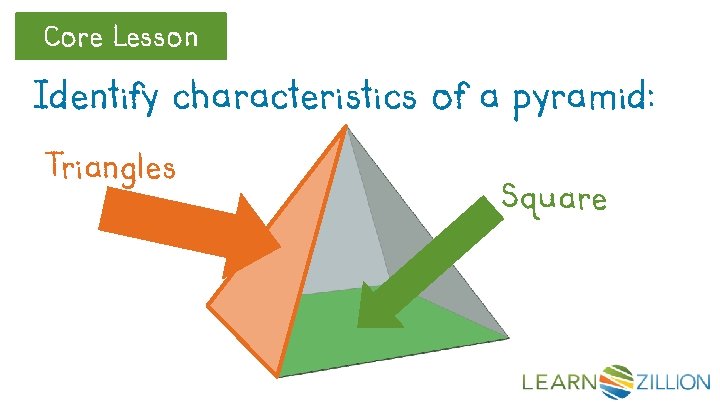
Core Lesson Identify characteristics of a pyramid: Triangles Square
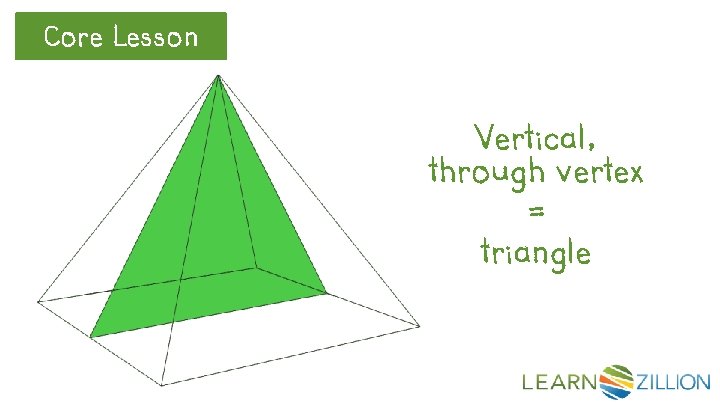
Core Lesson Vertical, through vertex = triangle

Core Lesson Effect of slicing plane We would see a trapezoid.

Core Lesson Horizontal Cross-section Slices parallel to the base will always be similar to the base
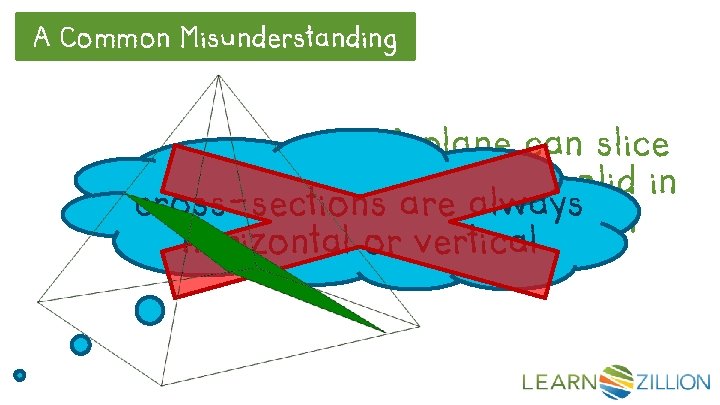
A Common Misunderstanding A plane can slice through a solid in cross-sections are always any direction horizontal or vertical

The Great Pyramids of Giza were originally built with a limestone cap at the top. Over the centuries, these caps have eroded away, and the tops of the pyramids are now parallel to the ground. What 2 D shape describes the new top of the pyramid?

The Great Pyramids of Giza were originally built with a limestone cap at the top. Over the centuries, these caps have eroded away, and the tops of the pyramids are now parallel to the ground. What 2 D shape describes the new top of the pyramid? Top of pyramid is square
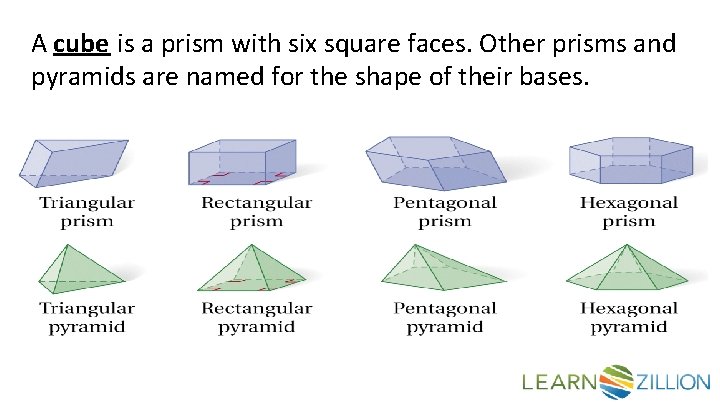
A cube is a prism with six square faces. Other prisms and pyramids are named for the shape of their bases.
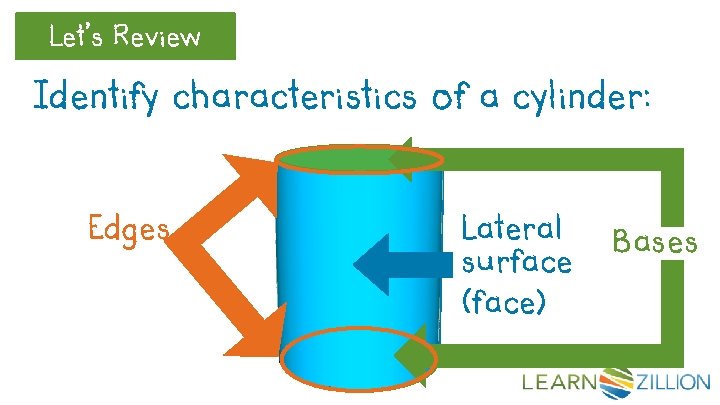
Let’s Review Identify characteristics of a cylinder: Edges Lateral surface (face) Bases
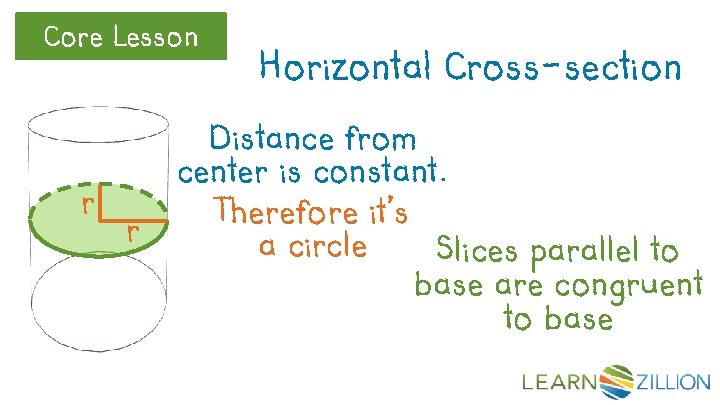
Core Lesson r r Horizontal Cross-section Distance from center is constant. Therefore it’s a circle Slices parallel to base are congruent to base
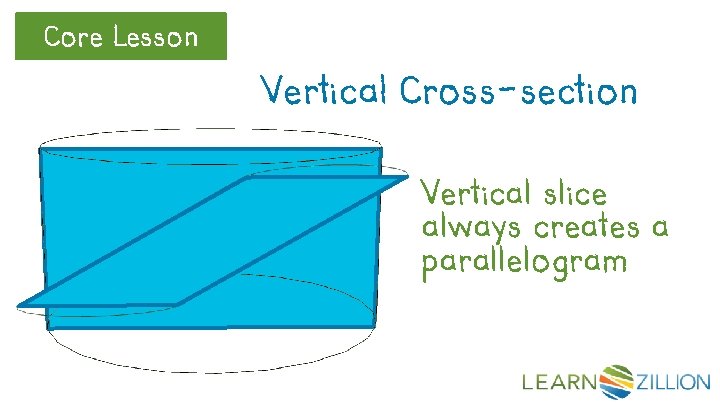
Core Lesson Vertical Cross-section Vertical slice always creates a parallelogram
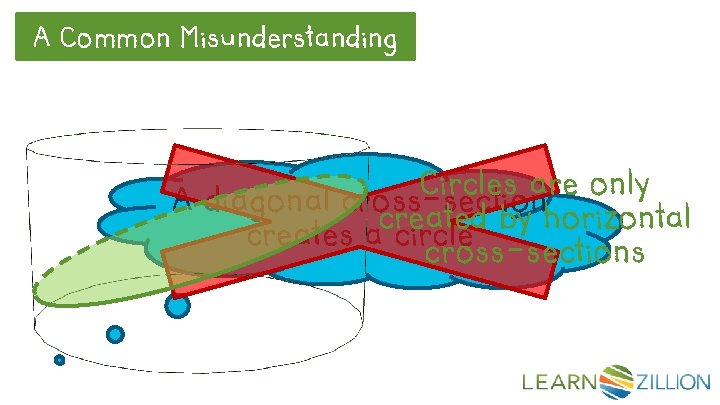
A Common Misunderstanding Circles are only A diagonal cross-section created by horizontal creates a circle cross-sections
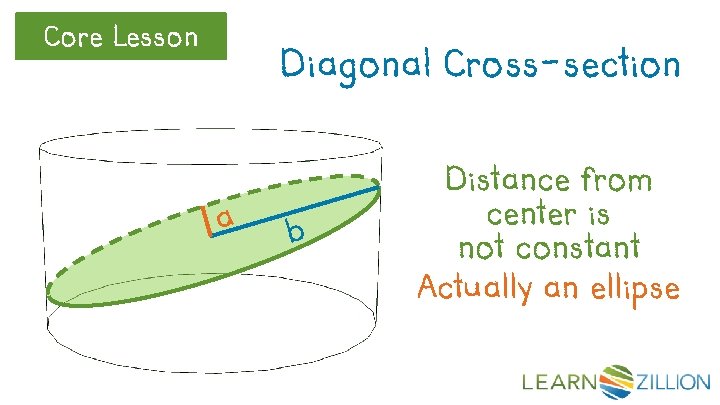
Core Lesson Diagonal Cross-section a b Distance from center is not constant Actually an ellipse

Ice cream factories test how consistently the ingredients are distributed through each carton by cutting cartons in half for a good view. Describe the 2 D figure that result from slicing a carton vertically through the top.

Core Lesson Ice cream factories test how consistently the ingredients are distributed through each carton by cutting cartons in half for a good view. Describe the 2 D figures that result from slicing a carton vertically through the top. Vertical: rectangle
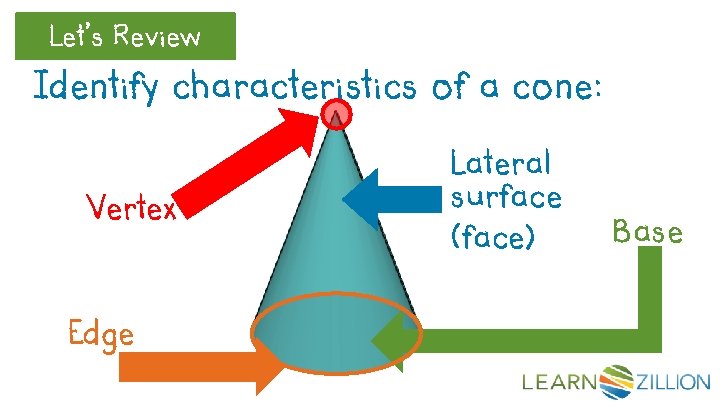
Let’s Review Identify characteristics of a cone: Vertex Edge Lateral surface (face) Base
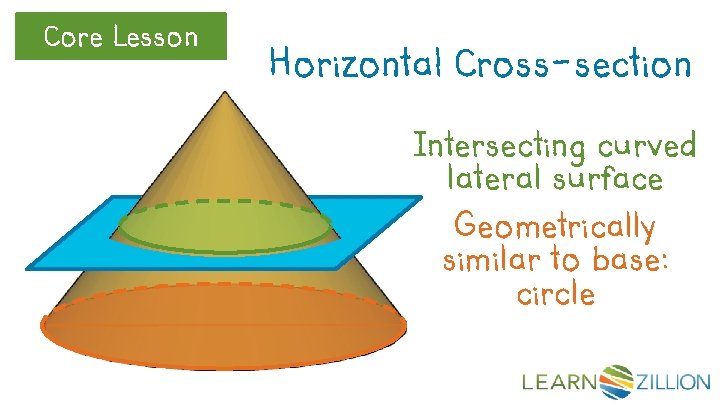
Core Lesson Horizontal Cross-section Intersecting curved lateral surface Geometrically similar to base: circle
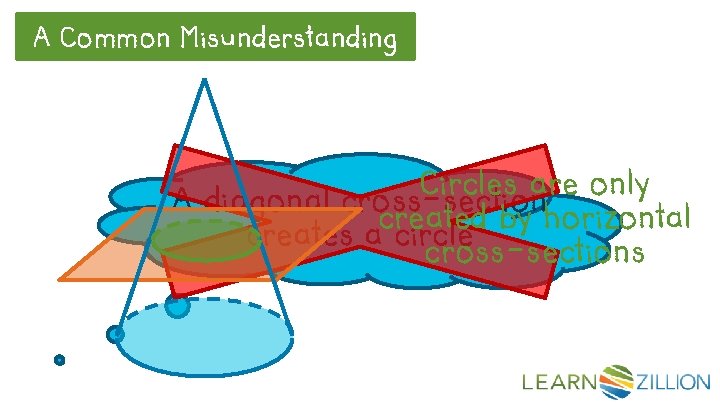
A Common Misunderstanding Circles are only A diagonal cross-section created by horizontal creates a circle cross-sections

Core Lesson a Diagonal Cross-section b Distance from center is not constant Actually an ellipse

Core Lesson Interactive

In this lesson, you will learn how to predict the 3 D results of rotating simple figures by analyzing the effects of rotations.

How do you predict the 3 D result of rotating a 2 D figure? What 3 D shape would result from rotating this rectangle?
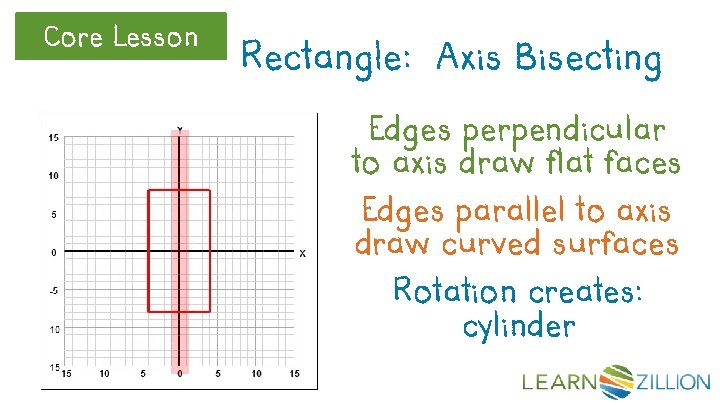
Core Lesson Rectangle: Axis Bisecting Edges perpendicular to axis draw flat faces Edges parallel to axis draw curved surfaces Rotation creates: cylinder

Core Lesson Rectangle: Axis Along Edges perpendicular to axis draw flat faces Edges parallel to axis draw curved surfaces Rotation creates: cylinder
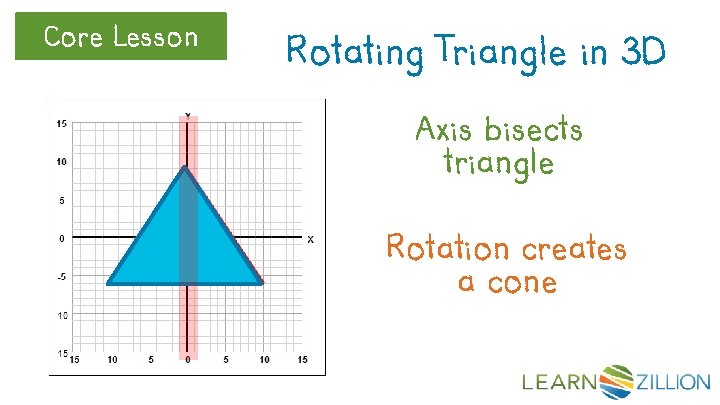
Core Lesson Rotating Triangle in 3 D Axis bisects triangle Rotation creates a cone
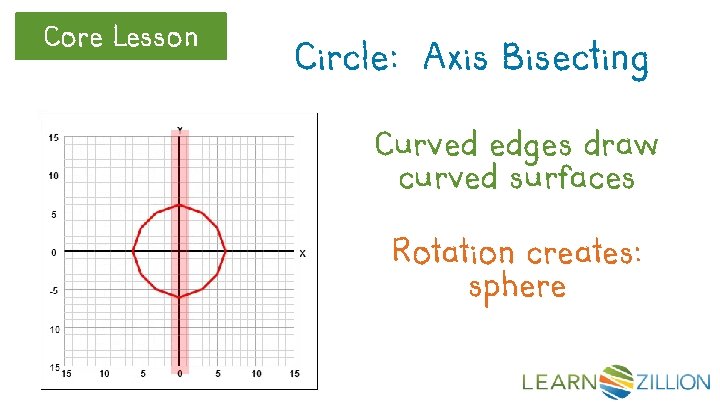
Core Lesson Circle: Axis Bisecting Curved edges draw curved surfaces Rotation creates: sphere

The End !!!
- Slides: 33