Three topics for the day Elementary Row Operations

Three topics for the day: Elementary Row Operations Row Echelon Form Reduced Row Echelon Form …in Sec. 7. 3 b

When using Gaussian Elimination, we work primarily on the coefficients of the variables. Knowing this, it is often easier to perform these operations on the matrix form of a system of equations… Example – the system: The augmented matrix: The coefficient matrix:

Definition: Row Echelon Form (REF) of a Matrix A matrix is in row echelon form if the following conditions are satisfied: 1. Rows consisting entirely of 0’s (if there any) occur at the bottom of the matrix. 2. The first entry in any row with nonzero entries is 1. 3. The column subscript of the leading 1 entries increases as the row subscript increases. Example: This should look somewhat familiar… Triangular Form? !? !

Elementary Row Operations on a Matrix A combination of the following operations will transform a matrix to row echelon form: 1. Interchange any two rows. Notation: R ij indicates interchanging the i-th and j-th rows 2. Multiply all elements of a row by a nonzero real number. Notation: k. R i indicates multiplying the i-th row by k 3. Add a multiple of one row to any other row. Notation: k. R i + R j indicates adding k times the i-th row to the j-th row

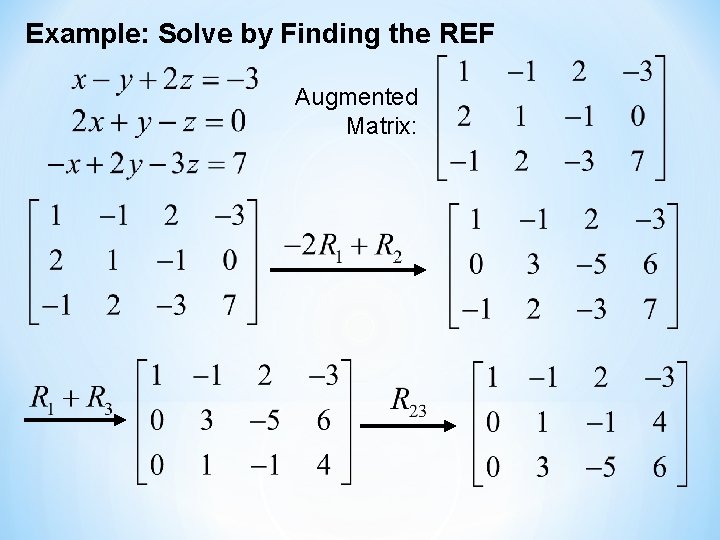
Example: Solve by Finding the REF Augmented Matrix:

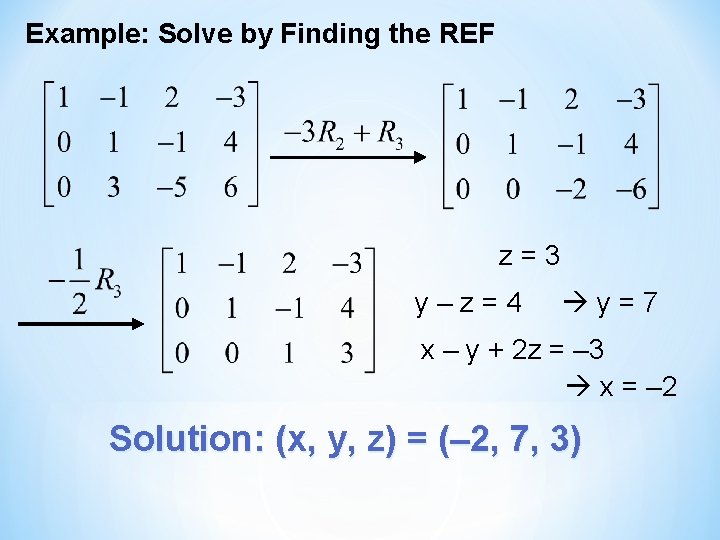
Example: Solve by Finding the REF z=3 y–z=4 y=7 x – y + 2 z = – 3 x = – 2 Solution: (x, y, z) = (– 2, 7, 3)

Guided Practice What elementary row operations applied to will yield the given matrix? 2 R 2 + R 1

Guided Practice What elementary row operations applied to will yield the given matrix? (1/4)R 3

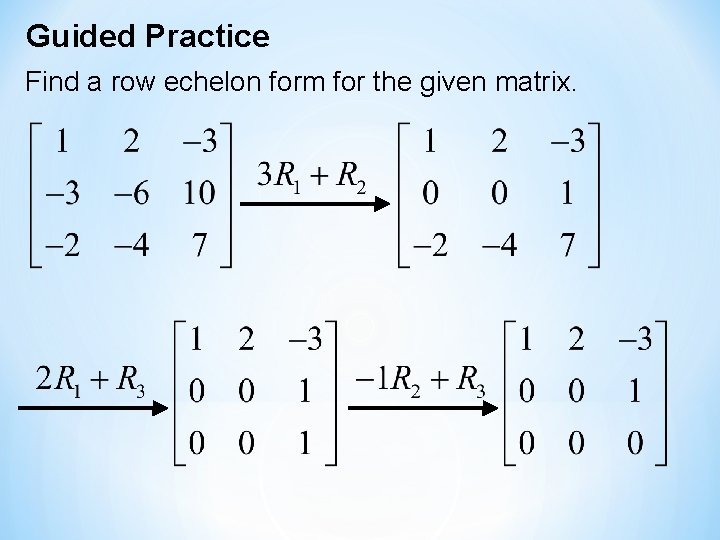
Guided Practice Find a row echelon form for the given matrix.

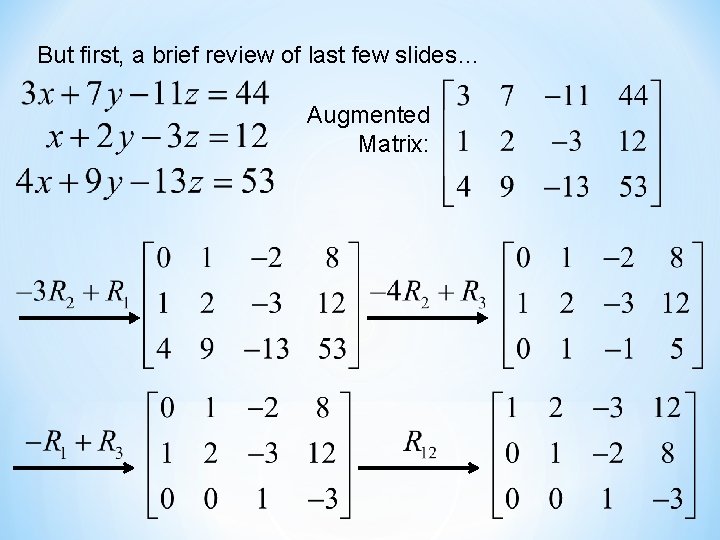
But first, a brief review of last few slides… Augmented Matrix:

But first, a brief review of the last few slides… z = – 3 y – 2 z = 8 y = 2 x + 2 y – 3 z = 12 x = – 1 Solution: (x, y, z) = (– 1, 2, – 3)

*Reduced Row Echelon Form It is possible to continue applying elementary row operations to a REF matrix until every column that has a leading 1 has 0’s elsewhere. This is the Reduced Row Echelon Form (RREF) of the matrix. Let’s see this with our previous example…

From this final RREF matrix, we can read the solution of (– 1, 2, – 3) directly… We can also use the Try it with our initial augmented matrix: calculator to find a RREF matrix…

More Good Examples Solve the system using a RREF matrix Augmented Matrix: RREF: (Calc) Solution: (x, y, z, w) = (2, 7, – 1, – 3)

More Good Examples Solve the system using a RREF matrix RREF Matrix: For every value of z, we can use these two equations to find a different x and y!!! Solution: Set of all ordered triples in the form (– 3 z + 5, 2 z – 2, z), where z is any real number

More Good Examples Solve the system using a RREF matrix Augmented Matrix: RREF Matrix: Solution: Set of all ordered 4 -tuples of the form (–z – 2 w + 1, 2 z + w – 1, z, w), z and w any real #’s