Three Dimensional Viewing Viewing Transformation We create a

Three Dimensional Viewing

Viewing Transformation • We create a 3 D scene using modelling transformations. We then ‘take a picture’ of the scene using a camera, • and display the camera’s picture on the display screen.

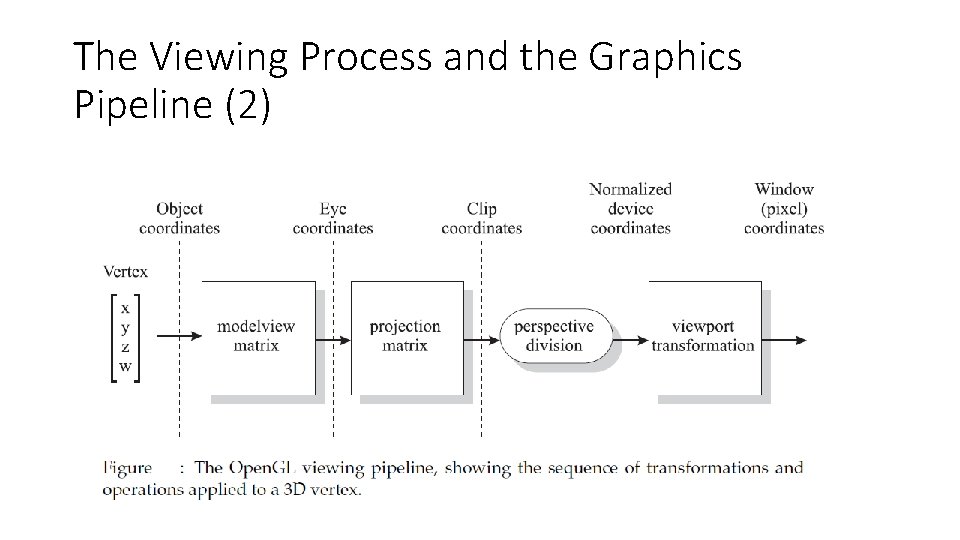
The Viewing Process and the Graphics Pipeline (2)

Projection

Projection • All our real world objects are 3 -dimensional. • But, when it comes to graphics or any other display device they are 2 dimensional. • The formal definition of projection is transformation of coordinate system of n dimensional object into an n-m dimension image where m≠ 0 • Thus simple projections can be obtained by discarding any one of dimension

Projections • Now that we’ve positioned and pointed the Open. GL camera, • the next step is to specify what kind of image we want. This is done using the projection matrix, P. • Open. GL applies the projection transformation after it has applied the modelview transformation.

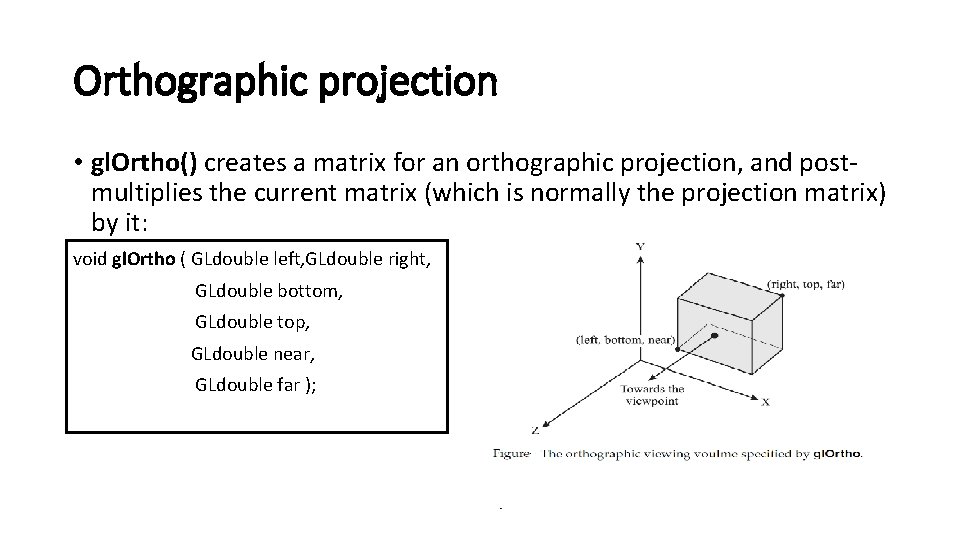
Orthographic projection When the direction of projection is perpendicular to the view plane and the projection plane is parallel to any one of the standard planes, XY plane, YZ palne or XZ plane then the projection is called orthographic projection

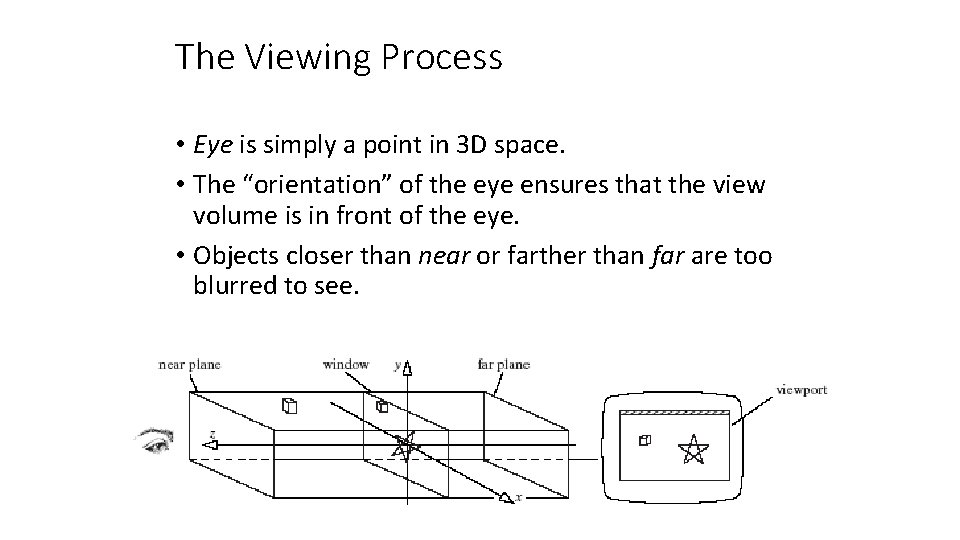
The Viewing Process • Eye is simply a point in 3 D space. • The “orientation” of the eye ensures that the view volume is in front of the eye. • Objects closer than near or farther than far are too blurred to see.

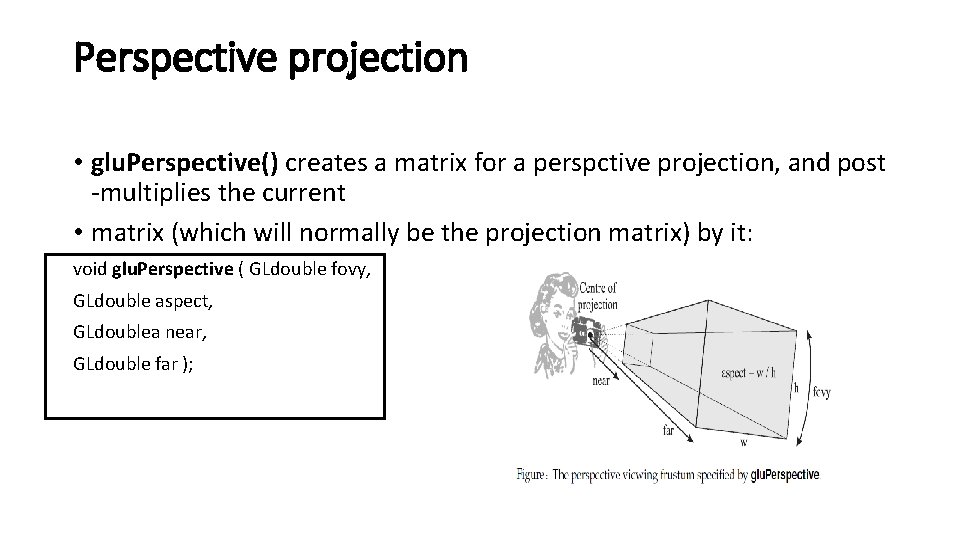
Perspective projection • In perspective projection there is always a point where all the projection lines converges. This point is called a center of projection.

View Volume • Consider the real world camera analogy, in which we choose the lens type (wide-angle, telephoto etc. ). • The choice of lens affects the field of view, and selects what portion of the 3 D world will appear within the bounds of final image. • The volume of space which eventually appears in the image is known as the view volume (or view frustum).

View Volume • The actual 3 D shape of the view volume depends on what kind of projection is used. • For orthographic (parallel) projections the view volume is box-shaped. • perspective projections have a view volume shaped like a truncated pyramid. • Its side walls are fixed by the window edges; its other two walls are fixed by a near plane and a far plane.

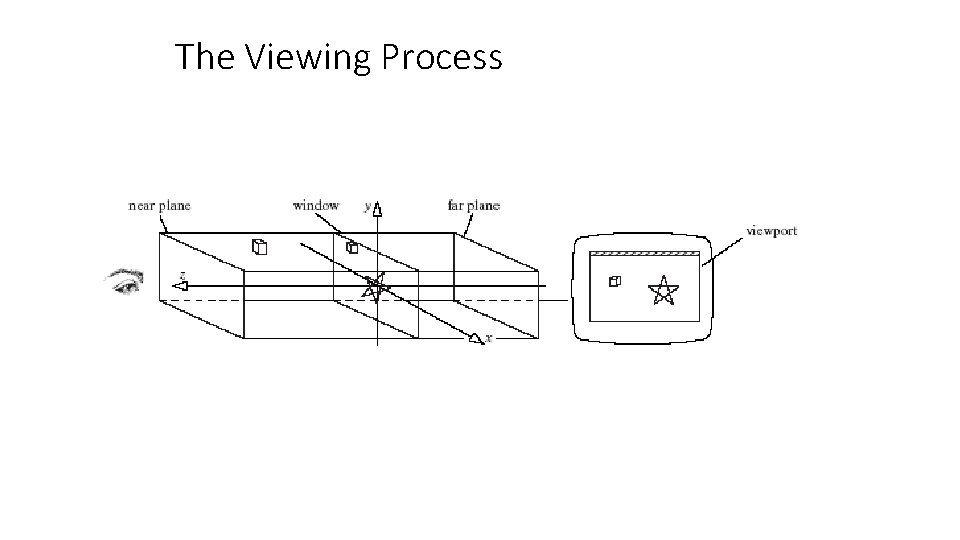
The Viewing Process

Drawing 3 D Scenes in Open. GL • We want to transform objects in order to orient and position them as desired in a 3 D scene. • Open. GL provides the necessary functions to build and use the required matrices. • The matrix stacks maintained by Open. GL make it easy to set up a transformation for one object, and then return to a previous transformation, in preparation for transforming another object.

The Camera in Open. GL • The camera is created with a matrix. • We will study the details of how this is done later. • For now, we just use an Open. GL tool to set up a reasonable camera so that we may pay attention primarily to transforming objects.

The Viewing Process and the Graphics Pipeline (4) • Points inside the view volume are projected onto the window along lines parallel to the z-axis. • We ignore their z-component, so that the 3 D point (x 1 y 1, z 1) projects to (x 1, y 1, 0). • Points lying outside the view volume are clipped off. • A separate viewport transformation maps the projected points from the window to the viewport on the display device.

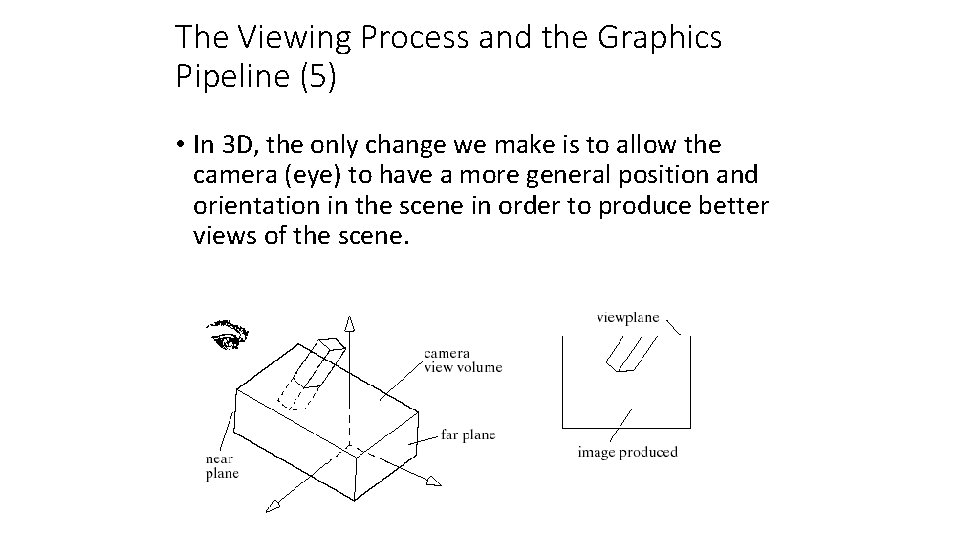
The Viewing Process and the Graphics Pipeline (5) • In 3 D, the only change we make is to allow the camera (eye) to have a more general position and orientation in the scene in order to produce better views of the scene.

The Viewing Process and the Graphics Pipeline (6) • The z axis points toward the eye. X and y point to the viewer’s right and up, respectively. • Everything outside the view volume is clipped. • Everything inside it is projected along lines parallel to the axes onto the window plane (parallel projection).

Setting Up the Camera (2) • What glu. Look. At does is create a camera coordinate system of three mutually orthogonal unit vectors: u, v, and n. • n = eye - look; u = up x n; v = n x u • Normalize n, u, v (in the camera system) and let e = eye - O in the camera system, where O is the origin.

Setting Up the Camera (3) • Then glu. Look. At () sets up the view matrix where d = (-e∙u, -e∙v, -e∙n) • up is usually (0, 1, 0) (along the y-axis), look is frequently the middle of the window, and eye frequently looks down on the scene.

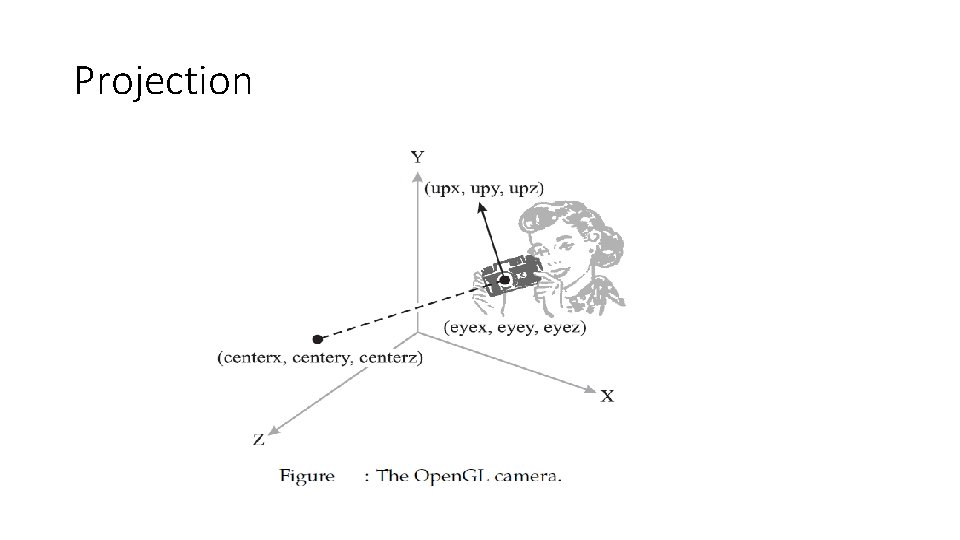
Controlling the camera • We set the position and orientation of the Open. GL camera, as shown in Figure 9. 2, using glu. Look. At(): • void glu. Look. At ( GLdouble eyex, GLdouble eyey, GLdouble eyez, GLdouble centerx, GLdouble centery, GLdouble centerz, GLdouble upx, GLdouble upy, GLdouble upz );

Controlling the camera • The position of the camera in space – sometimes also called the eyepoint – is given by (eyex, eyey, eyez). • (centerx, centery, centerz) specifies a look point for the camera to ‘look at’, and a good choice for this would a point of interest in the scene, and often the center of the scene is used. • Together, the points (eyex, eyey, eyez) and (centerx, centery, centerz) define a view vector. The last set of glu. Look. At()’s arguments specifythe up vector of the camera. This defines the camera’s orientation at the eyepoint.

Example gl. Matrix. Mode (GL_PROJECTION); // set the view volume (world coordinates) gl. Load. Identity(); gl. Ortho (-3. 2, -2. 4, 1, 50); gl. Matrix. Mode (GL_MODELVIEW); // place and aim the camera gl. Load. Identity (); glu. Look. At (4, 4, 4, 0, 1, 0); // modeling transformations go here

Orthographic projection • gl. Ortho() creates a matrix for an orthographic projection, and postmultiplies the current matrix (which is normally the projection matrix) by it: void gl. Ortho ( GLdouble left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble near, GLdouble far );

Perspective projection • glu. Perspective() creates a matrix for a perspctive projection, and post -multiplies the current • matrix (which will normally be the projection matrix) by it: void glu. Perspective ( GLdouble fovy, GLdouble aspect, GLdoublea near, GLdouble far );

Setting Up the Scene (2) gl. Matrix. Mode (GL_MODELVIEW); // set up the modelview matrix gl. Load. Identity (); // initialize modelview matrix // set up the view part of the matrix // do any modeling transformations on the scene

Setting Up the Projection gl. Matrix. Mode(GL_PROJECTION); // make the projection matrix current gl. Load. Identity(); // set it to the identity matrix gl. Ortho(left, right, bottom, top, near, far); // multiply it by the new matrix • Using 2 for near places the near plane at z = -2, that is, 2 units in front of the eye. • Using 20 for far places the far plane at -20, 20 units in front of the eye.

Setting Up the Camera (View Matrix) gl. Matrix. Mode (GL_MODELVIEW); // make the modelview matrix current gl. Load. Identity(); // start with identity matrix // position and aim the camera glu. Look. At (eye. x, eye. y, eye. z, // eye position look. x, look. y, look. z, // the “look at” point 0, 1, 0) // approximation to true up direction // Now do the modeling transformations

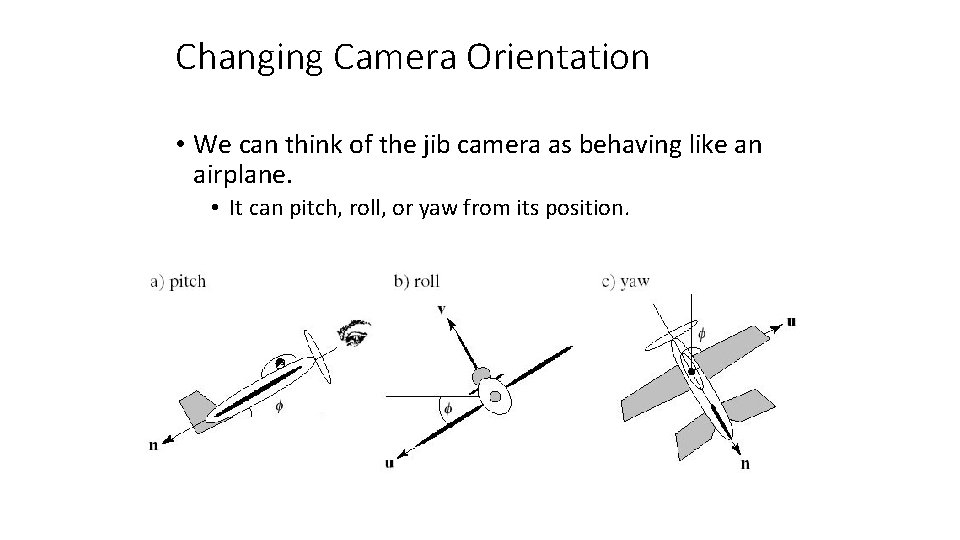
Changing Camera Orientation • We can think of the jib camera as behaving like an airplane. • It can pitch, roll, or yaw from its position.

Changing Camera Orientation (2) • Pitch – the angle between the longitudinal axis and world horizontal. • Roll – the angle between the transverse axis and the world. • Yaw – motion of the longitudinal axis causing a change in the direction of the plane’s flight.