Three different ways There are three different ways








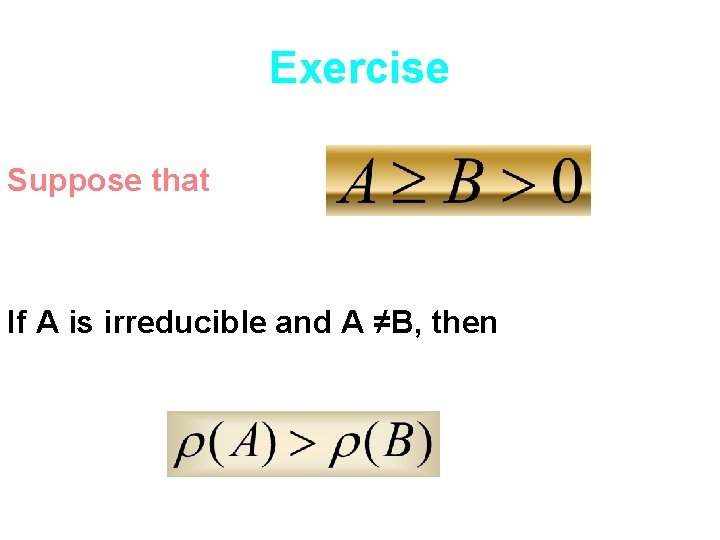






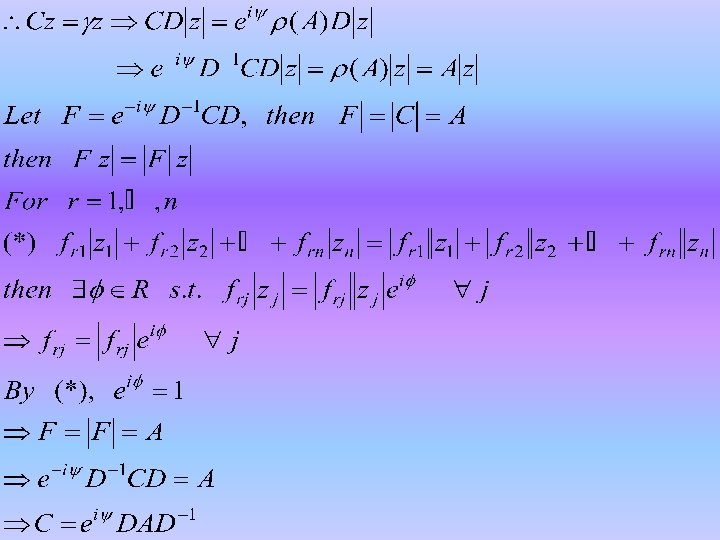






































































- Slides: 92

Three different ways There are three different ways to show that ρ(A) is a simple eigenvalue of an irreducible nonnegative matrix A:








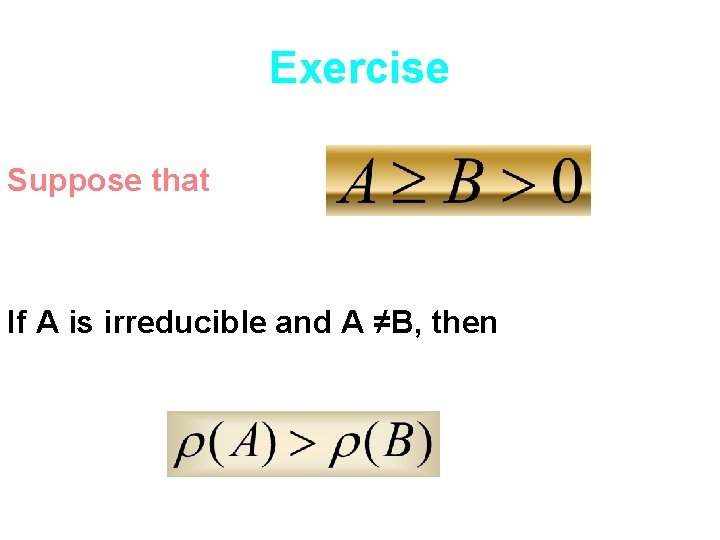
Exercise Suppose that If A is irreducible and A ≠B, then


Remark with equality iff the nonzero wis have the argument i. e. such that

Lemma 2. 4. 24 (Wielandt’s Lemma) p. 1 Let Suppose that A is irreducible, nonnegative, and (a) Then

Lemma 2. 4. 24 (Wielandt’s Lemma) p. 2 (b) Suppose that C has an eigenvalue then C is of the form where D is a diagonal matrix that satisfies


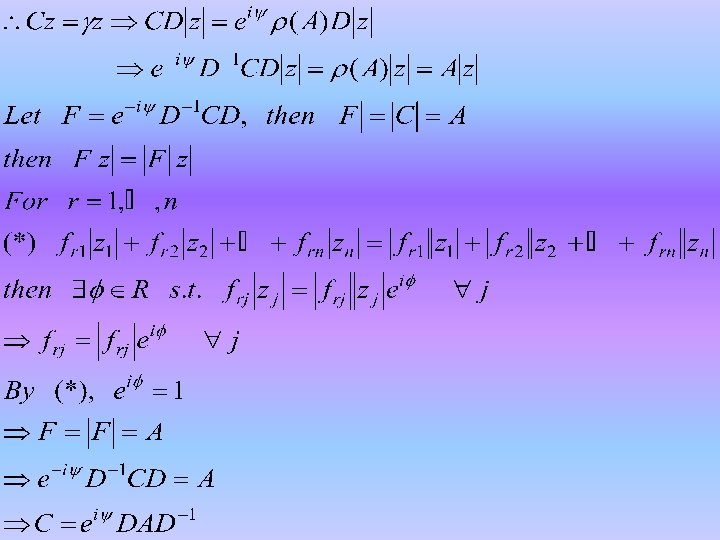

Exercise 2. 4. 25 (i) p. 1 and let k be a positive integer. Prove that where the equality holds if and only if


Exercise 2. 4. 25 p. 2 (i) Prove also that when the equality holds, the algebraic multiplicity of as an eigenvalue of A is equal to the algebraic multiplicity of as an eigenvalue of A.


Exercise 2. 4. 25 p. 3 (ii) Use the result of part (i), Theorem 2. 4. 4 and Perron’s theorem to deduce that if A is an irreducible nonnegative matrix , then is a simple eigenvalue of A.


Exercise 2. 4. 26 p. 1 (i) Let Prove that if and if A is irreducible then Hint: Use Remark 2. 4. 9.


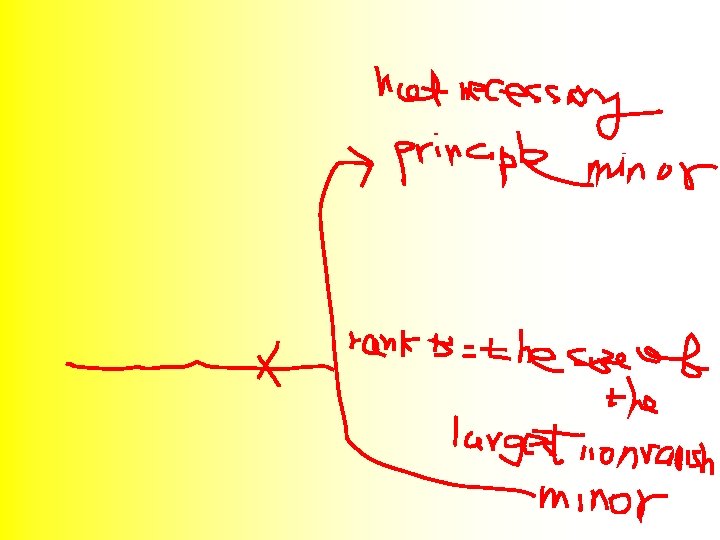
Exercise 2. 4. 26 p. 2 (ii) Use the result of part (i) to deduce that if A is an irreducible nonnegative matrix, then for any principal submatrix B of A, different from A.


Exercise 2. 4. 27 p. 1 Let be an irreducible nonnegative matrix. (i) Let B(t) =adj(t. I-A). By using the relation at t=ρ(A) and the fact that the geometric multiplicity of ρ(A) as an eigenvalue of A is 1, show that B(ρ(A)) is of the form where y, z are Perron vectors of A and respectively, and c is a nonzero real constant.


Exercise 2. 4. 27 p. 2 (ii)Show that where is the (n-1)-square principal submatrix obtained from A by deleting its row and column. (These relations are true for a general square complex matrix A. ) Then use the result of part (i) to deduce that and hence is a simple eigenvalue of A.




Exercise 2. 4. 27 p. 3 (iii) Using the fact that is equal to the largest real root of explain why cannot be negative. Deduce that


Exercise 2. 4. 28 Let be an irreducible nonnegative matrix. Let B(t) have the same meaning as given in Exercise 2. 4. 27. Use the result of Exercise 2. 4. 26 (ii) and the relation (which was established) to show that


Exercise 2. 4. 29 p. 1 Let A be an irreducible nonnegative matrix with index of imprimitivity h (i) Prove that trace(A)=0 whenever h>1




Exercise 2. 4. 29 p. 2 Let A be an irreducible nonnegative matrix with index of imprimitivity h (ii) Prove that h is a divisor of the number of nonzero eigenvalues of A (counting algebraic multiplicities)


Exercise 2. 4. 29 p. 3 Let A be an irreducible nonnegative matrix with index of imprimitivity h (iii) Prove that if A is nonsingular, nxn and n is a prime, then h=1 or n.


Theorem 2. 4. 22 (2 nd part of the Frobenius Thm) Given irreducible matrix with m distinct eigenvalues with moduloρ(A) Then (i) the peripheral spectrum of A is

Theorem 2. 4. 22 (2 nd part of the Frobenius Thm) (iii) If Apply Wielandt’s Lemma to prove

Another proof in next page



Fully Cyclic The peripheral spectrum of A is called fully cyclic if then corresponding to is an eigenvector of A for all integers k.

Fully Cyclic p. 2 Note that for k=0, the latter condition becomes

Corollary 2. 4. 30 Let A be an irreducible nonnegative matrix then the index of imprimitivity of A is equal to the spectral index of A.


Corollary 2. 4. 31 The peripheral spectrum of an irreducible nonnegative matrix is fully cyclic


Exercise 2. 4. 32 Let P be a square nonnegative matrix. Prove that the peripheral spectrum of P is fully cyclic if and only if P satisfies the following: If is a peripheral eigenvalue of P and z is a corresponding eigenvector, then


Theorem 2. 4. 33 If then there is a permutation matrix P such that Frobenius normal form where is 1 x 1 or is irreducible.


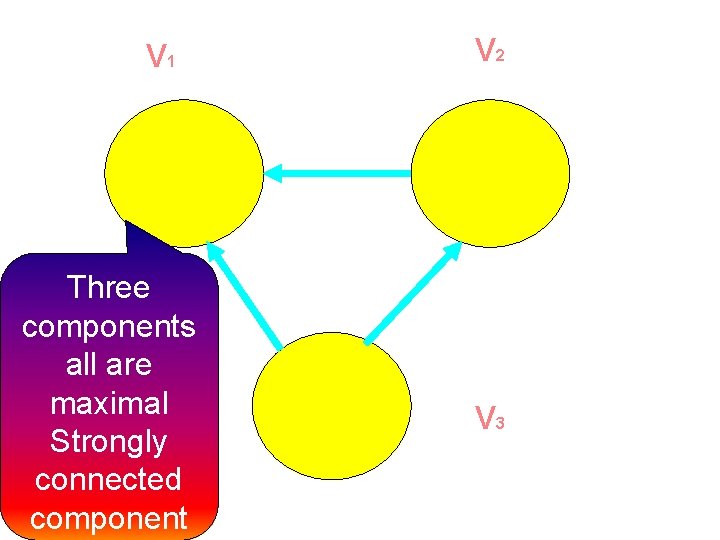
Example

V 1 Three components all are maximal Strongly connected component V 2 V 3

Remark p. 1 If A is reducible , nonnegative, and there is a permutation matrix P such that where is 1 x 1 or is irreducible.

Remark p. 2 then The peripheral eigenvalue of A is of the form of times a root of unity and

Theorem 2. 4. 34 Given A is primitive if and only if



Exercise 2. 4. 35 The spectral radius of a nonnegative matrix A is positive if and only if G(A) contains at least a circuit.

Exercise 2. 4. 36 (i) Find the Frobenius normal form of the matrix (ii) Compute

Exercise 2. 4. 37 Let A be an nxn irreducible nonnegative matrix and let Then there exists and a positive vector x such that where is defined to be

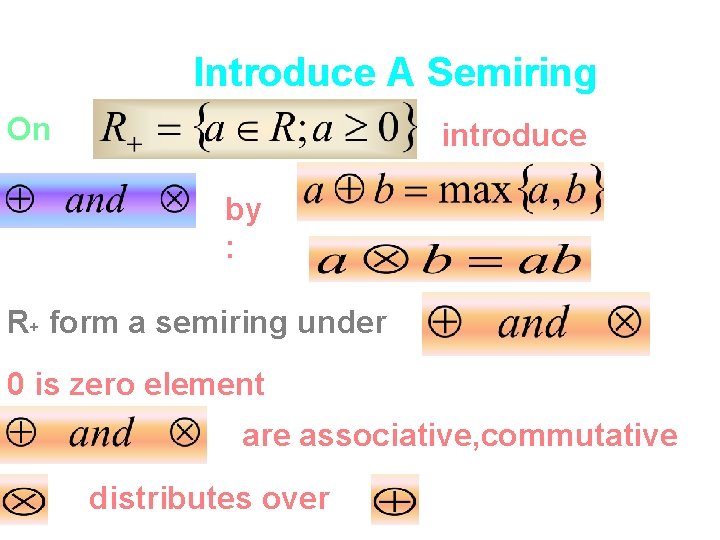
Introduce A Semiring On introduce by : R+ form a semiring under 0 is zero element are associative, commutative distributes over

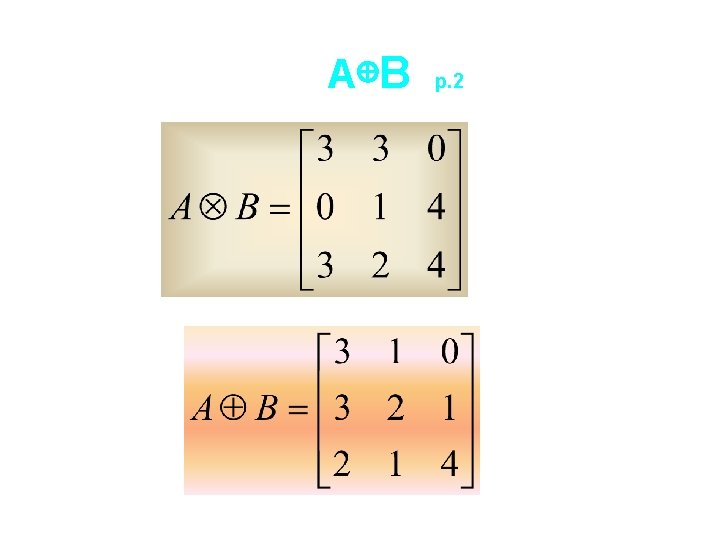
A⊕B p. 1

A⊕B p. 2

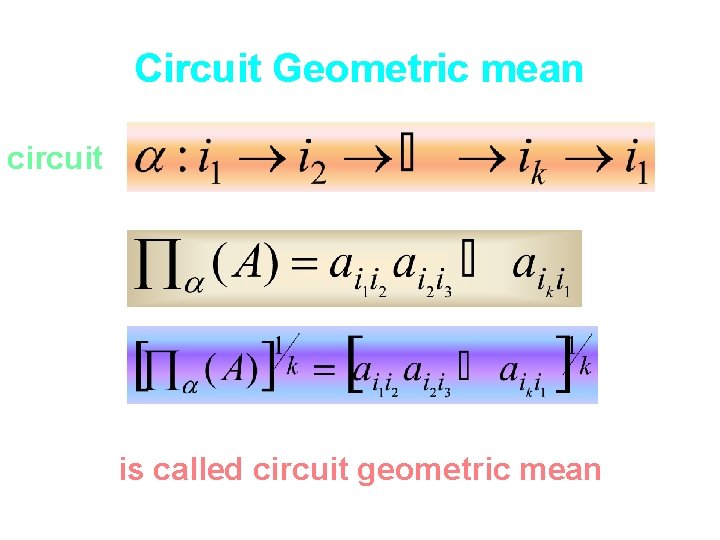
Circuit Geometric mean circuit is called circuit geometric mean

Lemma 2. 4. 38 Let A be an irreducible nonnegative γ is called a matrix max eigenvalue and x is a semipositive vectorthe and corresponding max eigenvector such that then where μ(A) is the maximum circuit geometric mean.




Plus max algebra R∪{-∞} They are isometric

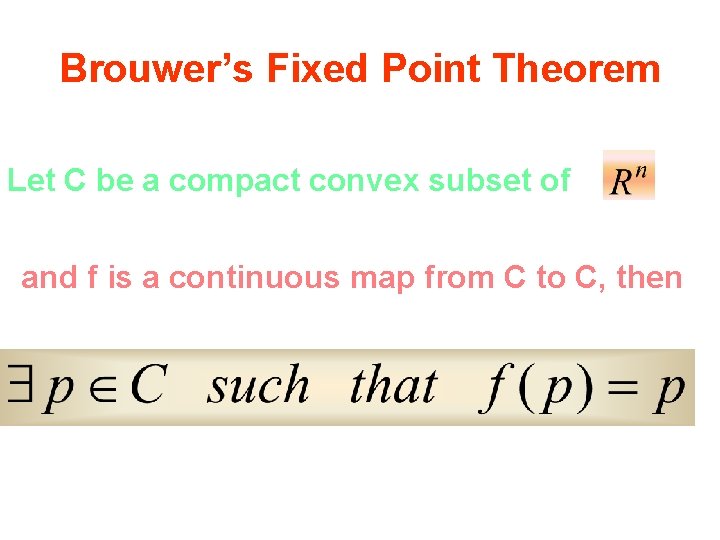
Brouwer’s Fixed Point Theorem Let C be a compact convex subset of and f is a continuous map from C to C, then

Theorem 2. 4. 39 Max version of the Perron-Frobenius Theorem If A be an irreducible nonnegative matrix then there is a positive vector x such that


Fact Given an irreducible nonnegative matrix A there is a diagonal matrix D with positive diagonal entries such that has the constant row sums.

Remark 2. 4. 40 Theorem 2. 4. 39 is equivalent to the assertion that given an irreducible nonnegative matrix A there is a diagonal matrix D with positive diagonal entries such that in the maximum entry in each row is the same.


Let k be a fixed positive integer, If , then let us define the sum of the k largest components in then

Let k be a fixed positive integer, If , then let us define by then

Theorem 2. 4. 41 Let A be an irreducible nonnegative matrix and let Then there exists a positive vector x and a constant such that


Remark p. 2 Let X be a Topology space, F is a Banach space and is continuous map such that T(X) is precompact in F. Then for any map there is a continuous of finite rank s. t.

Combinatorial Spectral Theory of Nonnegative Matrices
