This is the degree of accuracy how accurate

Exactly how accurate? Lesson Objective To realise that answers in Mathematics are often not

Key Words The lowest value something is before rounding What something is rounded to

Answer these questions How old are you? What time is it? What’s the span

Degrees of Accuracy Quite often, we see numbers that aren’t exact. What is the

Bounds What is the lowest, and highest, values that this number could be if

What is the fastest possible time Usain Bolt completed the 100 m in? 9.

Rounding Error So, the exact value of our number could be anything between 59.

Effect on calculations 69. 5 cm 70 cm The dimensions are measured to the

69. 5 cm 70 cm 94. 5 cm 95 cm Work out the upper

#harrismaths Someone has missed the lesson. Write a tweet (or two) telling them what

Slides: 12

Download presentation

This is the degree of accuracy (how accurate an answer is) Starter Round to 1 decimal place 1) 5. 18 5. 2 5 2) 15. 09 15. 1 20 3) 187. 55 187. 6 200 4) 90. 05 90. 1 90 5) 8. 97 9. 0 9 6) 6. 49 6. 5 6 Extension: Round to 1 significant figure. This is also a degree of accuracy

Exactly how accurate? Lesson Objective To realise that answers in Mathematics are often not exact

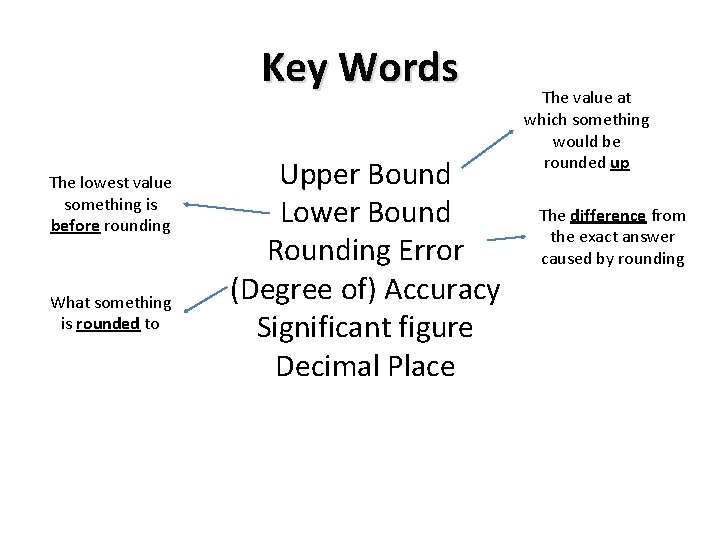
Key Words The lowest value something is before rounding What something is rounded to Upper Bound Lower Bound Rounding Error (Degree of) Accuracy Significant figure Decimal Place The value at which something would be rounded up The difference from the exact answer caused by rounding

Answer these questions How old are you? What time is it? What’s the span of your hand? What is the value of π? How many students in this class? How many students in the whole school? How accurate are your answers?

Degrees of Accuracy Quite often, we see numbers that aren’t exact. What is the degree of accuracy here? The time is shown to 2 decimal places

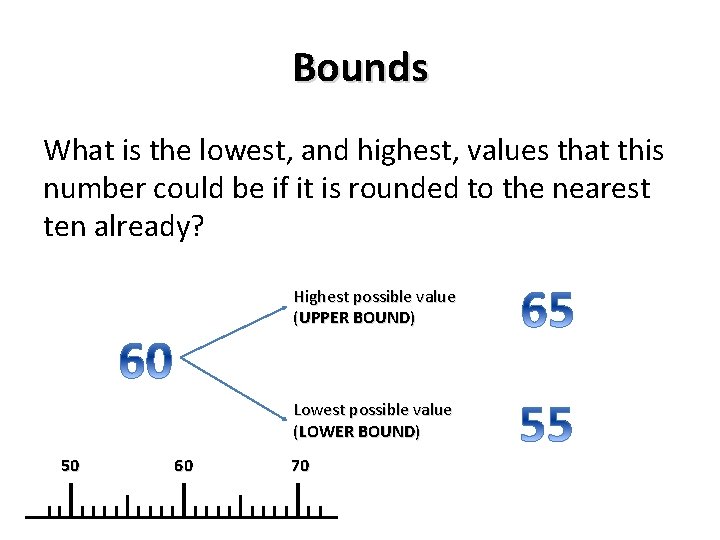
Bounds What is the lowest, and highest, values that this number could be if it is rounded to the nearest ten already? Highest possible value (UPPER BOUND) Lowest possible value (LOWER BOUND) 50 60 70

Bounds What is the lowest, and highest, values that this number could be if it is actually rounded to the nearest whole number already? Highest possible value (UPPER BOUND) Lowest possible value (LOWER BOUND) 59 60 61

What is the fastest possible time Usain Bolt completed the 100 m in? 9. 575 seconds 9. 585 seconds What is the slowest? Extension: What would his fastest/slowest speed be? (assume the 100 m track is exactly 100 m – what would be the effect if it was measured to the nearest meter? ? )

Rounding Error So, the exact value of our number could be anything between 59. 5 – 60. 5 What effect could this have when we come to do some calculations?

Effect on calculations 69. 5 cm 70 cm The dimensions are measured to the nearest cm 94. 5 cm 95 cm Work out the upper and lower bounds for each dimension

69. 5 cm 70 cm 94. 5 cm 95 cm Work out the upper and lower bounds for the perimeter Extension – Work out the upper and lower bounds for the area of the screen Perimeter Upper Bound – 332 cm Lower Bound – 328 cm Area UB – 6732. 75 cm² LB – 6567. 75 cm²

#harrismaths Someone has missed the lesson. Write a tweet (or two) telling them what they missed and what you learned today.