Thinking Mathematically Seventh Edition Chapter 2 Set Theory




























- Slides: 30

Thinking Mathematically Seventh Edition Chapter 2 Set Theory Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 1

Section 2. 1 Basic Set Concepts Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 2

Objectives 1. Use three methods to represent sets. 2. Define and recognize the empty set. 3. Use the symbols and 4. Apply set notation to sets of natural numbers. 5. Determine a set’s cardinal number. 6. Recognize equivalent sets. 7. Distinguish between finite and infinite sets. 8. Recognize equal sets. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 3

Sets A set is collection of objects whose contents can be clearly determined. Elements or members are the objects in a set. A set must be well-defined, meaning that its contents can be clearly determined. The order in which the elements of the set are listed is not important. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 4

Methods for Representing Sets Capital letters are generally used to name sets. A word description can designate or name a set. Use W to represent the set of the days of the week. Use the roster method to list the members of a set. Commas are used to separate the elements of the set. Braces, are used to designate that the enclosed elements form a set. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 5

Example 1: Representing a Set Using a Description Write a word description of the set: Solution Set P is the set of the first five presidents of the United States. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 6

Example 2: Representing a Set Using the Roster Method Write using the roster method: Set C is the set of U. S. coins with a value of less than a dollar. Express this set using the roster method. Solution Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 7

Set-Builder Notation We read this notation as “Set W is the set of all elements x such that x is a day of the week. ” Before the vertical line is the variable x, which represents an element in general. After the vertical line is the condition x must meet in order to be an element of the set. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 8

Example 3: Converting from Set. Builder to Roster Notation Express set using the roster method. Solution There are two months, namely March and May. Thus, Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 9

The Empty Set The empty set, also called the null set, is the set that contains no elements. The empty set is represented by These are examples of empty sets: Set of all numbers less than 4 and greater than 10 Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 10

Example 4: Recognizing the Empty Set (1 of 2) Which of the following is the empty set? a. No. This is a set containing one element. b. 0 No. This is a number, not a set. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 11

Example 4: Recognizing the Empty Set (2 of 2) Which of the following is the empty set? c. No. This set contains all numbers that are either less than 4, such as 3, or greater than 10, such as 11. d. Yes. There are no squares with three sides. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 12

Notations for Set Membership The Notations and The symbol is used to indicate that an object is an element of a set. The symbol is used to replace the words “is an element of. ” The symbol is used to indicate that an object is not an element of a set. The symbol the words” is not an element of. ” is used to replace Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 13

Example 5: Using the Symbols Epsilon and Epsilon Crossed Out Determine whether each statement is true or false: a. True b. True c. False. is a set and the set is not an element of the set Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 14

Sets of Natural Numbers The Set of Natural Numbers The three dots, or ellipsis, after the 5 indicate that there is no final element and that the list goes on forever. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 15

Example 6: Representing Sets of Natural Numbers Express each of the following sets using the roster method: a. Set A is the set of natural numbers less than 5. b. Set B is the set of natural numbers greater than or equal to 25. c. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 16

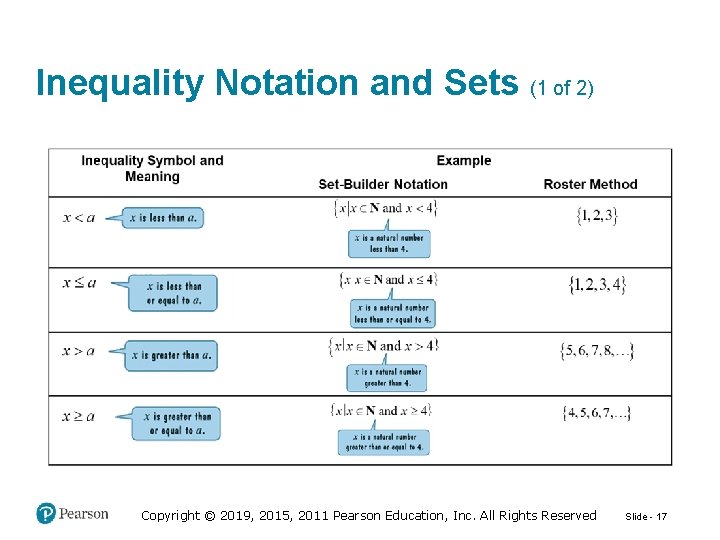
Inequality Notation and Sets (1 of 2) Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 17

Inequality Notation and Sets (2 of 2) Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 18

Example 7: Representing Sets of Natural Numbers Express each of the following sets using the roster method: a. Solution: b. Solution: Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 19

Cardinality and Equivalent Sets Definition of a Set’s Cardinal Number The cardinal number of a set A, represented by is the number of distinct elements in set A. The symbol is read “n of A. ” Repeating elements in a set neither adds new elements to the set nor changes its cardinality. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 20

Example 8: Cardinality of Sets Find the cardinal number of each of the following sets: a. b. c. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 21

Equivalent Sets (1 of 3) Definition of Equivalent Sets Set A is equivalent to set B means that set A and set B contain the same number of elements. For equivalent sets, Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 22

Equivalent Sets (2 of 3) These are equivalent sets: The line with arrowheads, indicate that each element of set A can be paired with exactly one element of set B and each element of set B can be paired with exactly one element of set A. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 23

Equivalent Sets (3 of 3) One-to-One Correspondences and Equivalent Sets 1. If set A and set B can be placed in one-to-one correspondence, then A is equivalent to B: 2. If set A and set B cannot be placed in one-to-one correspondence, then A is not equivalent to B: Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 24

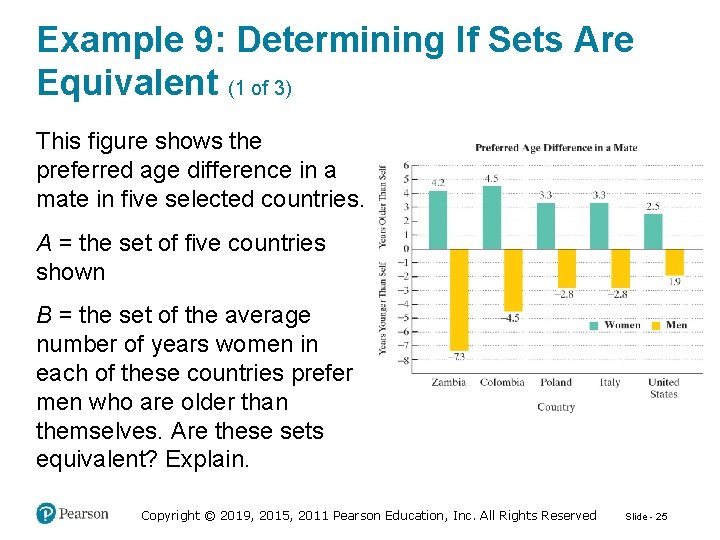
Example 9: Determining If Sets Are Equivalent (1 of 3) This figure shows the preferred age difference in a mate in five selected countries. A = the set of five countries shown B = the set of the average number of years women in each of these countries prefer men who are older than themselves. Are these sets equivalent? Explain. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 25

Example 9: Determining If Sets Are Equivalent (2 of 3) Method 1: Trying to set up a One-to-One Correspondence. Solution: The lines with the arrowheads indicate that the correspondence between the sets is not one-to-one. The elements Poland Italy from set A are both paired with the element 3. 3 from set B. These sets are not equivalent. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 26

Example 9: Determining If Sets Are Equivalent (3 of 3) Method 2: Counting Elements Solution: Set A contains five distinct elements: Set B contains four distinct elements: Because the sets do not contain the same number of elements, they are not equivalent. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 27

Finite and Infinite Sets Finite Sets and Infinite Sets Set A is a finite set if (that is, A is the empty set) or is a natural number. A set whose cardinality is not 0 or a natural number is called as infinite set. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 28

Equal Sets Definition of Equality of Sets Set A is equal to set B means that set A and set B contain exactly the same elements, regardless of order or possible repetition of elements. We symbolize the equality of sets A and B using the statement A = B. Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 29

Example 10: Determining Whether Sets Are Equal Determine whether each statement is true or false: a. True b. False Copyright © 2019, 2015, 2011 Pearson Education, Inc. All Rights Reserved Slide - 30
 Thinking mathematically 7th edition
Thinking mathematically 7th edition Open ended maths activities peter sullivan pdf
Open ended maths activities peter sullivan pdf Thinking mathematically john mason
Thinking mathematically john mason 3 layers of muscle
3 layers of muscle Chords rule in dbms
Chords rule in dbms Principles of information systems, seventh edition
Principles of information systems, seventh edition Molecular biology of the cell seventh edition
Molecular biology of the cell seventh edition Biology seventh edition
Biology seventh edition Total set awareness set consideration set
Total set awareness set consideration set Training set validation set test set
Training set validation set test set Example of universal existential statement in mathematics
Example of universal existential statement in mathematics Mathematically similar
Mathematically similar Growing mathematically
Growing mathematically Express magnetic flux mathematically
Express magnetic flux mathematically Speaking mathematically
Speaking mathematically Speaking mathematically variables
Speaking mathematically variables State heisenberg's uncertainty principle class 11
State heisenberg's uncertainty principle class 11 Introduction to triads and seventh chords
Introduction to triads and seventh chords Using mis 10th edition
Using mis 10th edition Report
Report Clear thinking and writing answer key
Clear thinking and writing answer key Positive thinking vs negative thinking examples
Positive thinking vs negative thinking examples Thinking about your own thinking
Thinking about your own thinking Holistic judgement
Holistic judgement Perbedaan critical thinking dan creative thinking
Perbedaan critical thinking dan creative thinking Thinking about you thinking about me
Thinking about you thinking about me Bounded set vs centered set
Bounded set vs centered set Crisp set vs fuzzy set
Crisp set vs fuzzy set Crisp set vs fuzzy set
Crisp set vs fuzzy set Crisp set vs fuzzy set
Crisp set vs fuzzy set What is the overlap of data set 1 and data set 2?
What is the overlap of data set 1 and data set 2?