Thi t k s Gi i thi u

Thiê t kê sô Giơ i thiê u vê ma ch sô : Tô ng hơ p ma ch du ng AND, OR va NOT Ngươ i tri nh ba y: Tiến sỹ Hoa ng Ma nh Thă ng

Vi du thiê t kê ma ch logic �Thiê t kê ma ch logic vơ i mô t đâ u ra f va 3 đâ u va o: x, y, z �f(x, y, x)=1 nê u x=1 đô ng thơ i vơ i y=1 hoă c z=1 hoă c ca hai �Ca c tô hơ p co thê : �x=1, y=1, z=1 xyz �x=1, y=1, z=0 xyz’ �x=1, y=0, z=1 xy’z �Ha m f(x, y, z) đươ c viê t dươ i da ng tô ng cu a ca c ti ch: f(x, y, z)=xyz+xyz’+xy’z Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 2

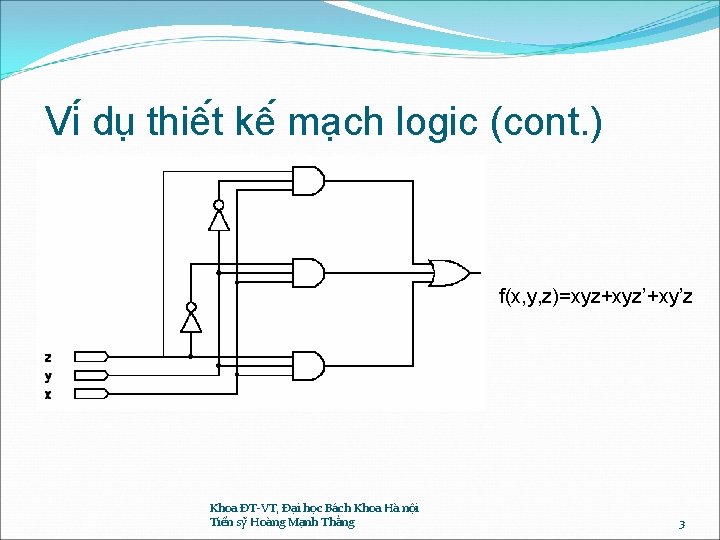
Vi du thiê t kê ma ch logic (cont. ) f(x, y, z)=xyz+xyz’+xy’z Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 3

Vi du thiê t kê ma ch logic (cont. ) �Thư c hiê n ma ch cho ha m f(x, y, z)=xyz+xyz’+xy’z như trên la đu ng, nhưng chưa pha i la đơn gia n nhâ t �Tư 14. a f(x, y, z)=xy+xy’z �Tư 12. a f(x, y, z)=x(y+y’z) � Tư 16. a f(x, y, z)=x(y+z) Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 4

Vi du thiê t kê ma ch logic (cont. ) �Dê thâ y ră ng, ma ch na y co chi phi (cô ng logic va kê t nô i) thâ p hơn ma ch cu ng chư c năng đươ c đưa ra lúc trươ c �Qua tri nh ta o ra ma ch tư ha m thê hiê n chư c năng go i la tô ng hơ p ma ch �Viê c ta o ma ng du ng ca c cô ng AND-OR tư ba ng chân lý la mô t trong nhiê u ky thuâ t tô ng hơ p đươ c du ng nhiê u sau na y Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 5

Tô ng hơ p ma ch logic �Nê u mô t ha m f đươ c mô ta bơ i ba ng chân ly thi biê u thư c ta o ra ha m f co thê đươ c nhâ n la i bă ng ca ch: �Xe t tâ t ca ca c tô hơ p ơ đo co f=1, hoă c �Xe t tâ t ca ca c tô hơ p ơ đo co f=0, �Đây la mô t ư ng du ng cu a ti nh đô i ngâ u Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 6

Minterms �Đô i vơ i mô t ha m co n biê n, f(. . . ), mô t minterm cu a f la ti ch cu a n biê n, trong đo mô i biê n xuâ t hiê n mô t lâ n dươ i da ng bâ t ky (nguyên biê n hoă c nghi ch đa o cu a biê n), nhưng không pha i ca hai �f(a, b, c) – vi du minterm la : abc, a’bc, abc’ �f(a, b, c) – vi du không pha i la minterm: ab, c’, a’c, �Mô t ha m n biê n co 2 n minterm Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 7

Minterms Sô ha ng �Mô i ha ng cu a ba ng ư ng vơ i mô t minterm �Khi mô t ha m đươ c viê t dươ i da ng tô ng ca c minterm thi da ng đo đươ c go i la chuâ n tô ng cu a ca c ti ch (Sum-Of. Product-SOP) Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 8

Biểu diễn hàm dùng minterm �Mô t ha m co thê đươ c biê u diê n dươ i da ng tô ng cu a ca c minterm Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 9

Ca c biê u diê n dùng minterm �Viê t ky hiê u theo minterm va ngươ c la i cu a ca ha m sau: �f(a, b, c)=abc+a’bc+abc’+a’b’c �f(a, b, c)=Σm(1, 5, 6, 7) Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 10

Tô ng hơ p logic �Ti nh đô i ngâ u gơ i y ră ng: nê u co thê tô ng hơ p mô t ha m f bă ng ca ch xem xe t ca c ha ng co f=1 thi cu ng co thê tô ng hơ p ha m đo bă ng ca ch xem xe t ca c ha ng co f=0 �Theo ca ch du ng nghi ch đa o ca c minterm, no đươ c go i la maxterm Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 11

Maxterms Sô ha ng �Mô i ha ng cu a ba ng tương ư ng vơ i mô t maxterm �Khi mô t ha m đươ c viê t dươ i dang ti ch cu a ca c maxterm thi no đươ c go i la chuâ n ti ch cu a ca c tô ng (Product-Of-Sum) Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 12

Biê u diê n dươ i da ng maxterm �Mô t ha m co thê đươ c biê u diê n dươ i da ng tô ng cu a ca c maxterm Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 13

Ca c vi du cho biê u diê n maxterm �Viê t ky hiê u theo minterm va ngươ c la i cu a ca ha m sau: �f(a, b, c)=(a+b+c)(a’+b+c)(a+b+c’)(a’+b’+c) �f(a, b, c)= πM(1, 5, 6, 7) Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 14

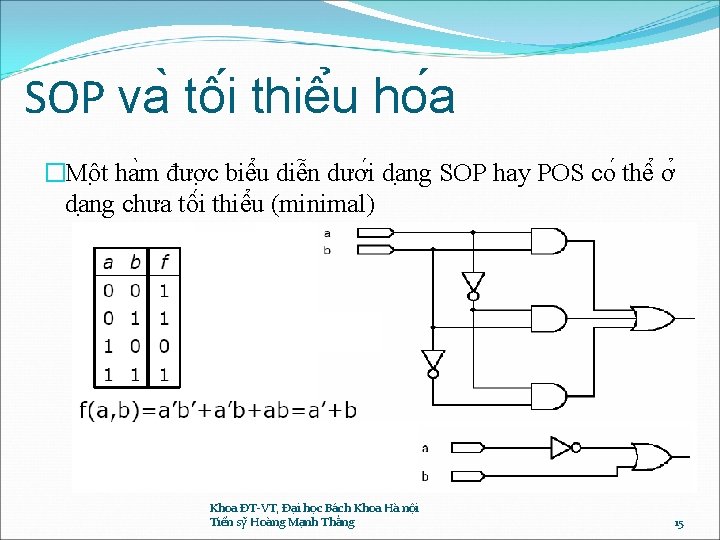
SOP va tô i thiê u ho a �Mô t ha m đươ c biê u diê n dươ i da ng SOP hay POS co thê ơ da ng chưa tô i thiê u (minimal) Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 15

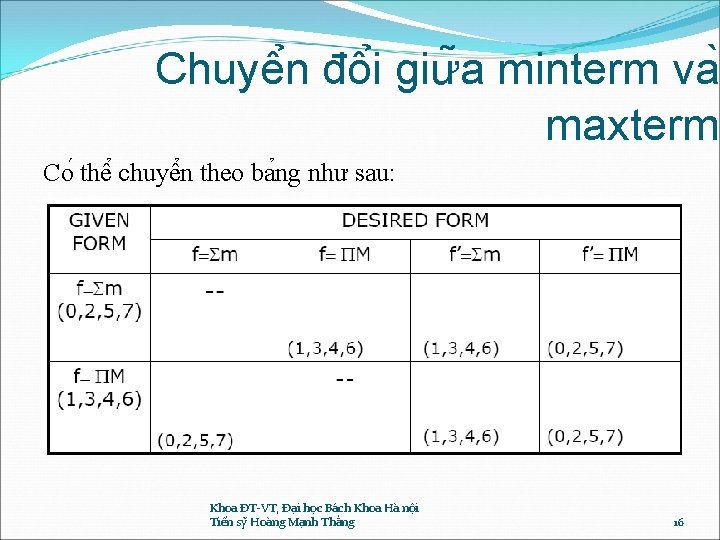
Chuyê n đô i giư a minterm va maxterm Co thê chuyê n theo ba ng như sau: (3 biê n) Du ng ca c sô vă ng mă t trong danh sa ch minterm Du ng ca c sô vă ng mă t trong danh sa ch maxterm Du ng ca c sô vă ng mă t trong danh sa ch minterm Du ng ca c sô trong danh sa ch maxterm Du ng ca c sô vă ng mă t trong danh sa ch maxterm Khoa ĐT-VT, Đại học Bách Khoa Hà nội Tiến sỹ Hoàng Mạnh Thắng 16