Thermodynamics of Gauge Theory from Gradient Flow For


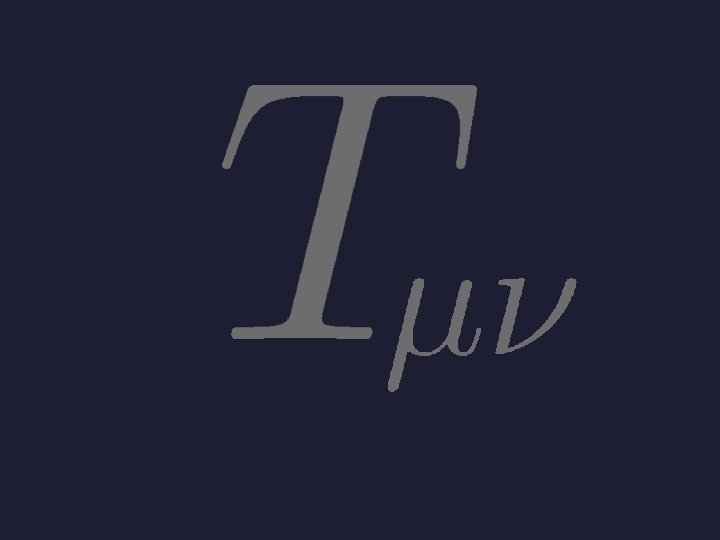
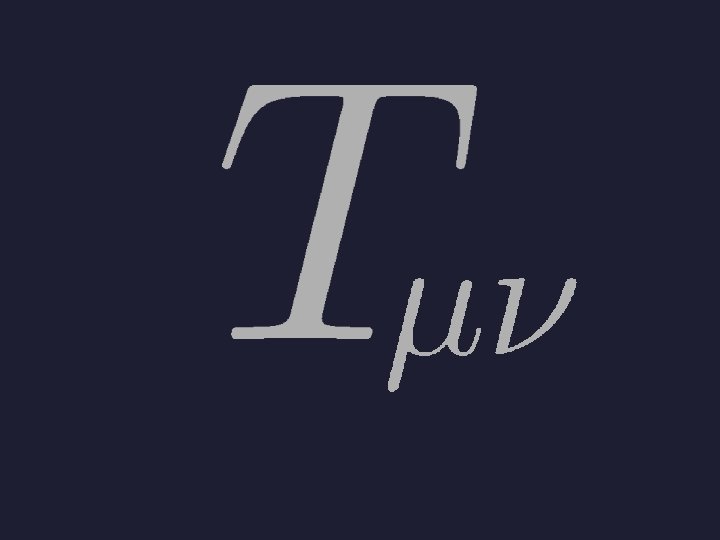












![YM Gradient Flow t: “flow time” dim: [length 2] Luescher, 2010 A. Ramos, plenary, YM Gradient Flow t: “flow time” dim: [length 2] Luescher, 2010 A. Ramos, plenary,](https://slidetodoc.com/presentation_image_h2/7b35ce797be5dc4dc33038533196ce27/image-19.jpg)
























- Slides: 55

Thermodynamics of Gauge Theory from Gradient Flow For Flow. QCD Collaboration

Thermodynamics of Gauge Theory from Gradient Flow For Flow. QCD Collaboration
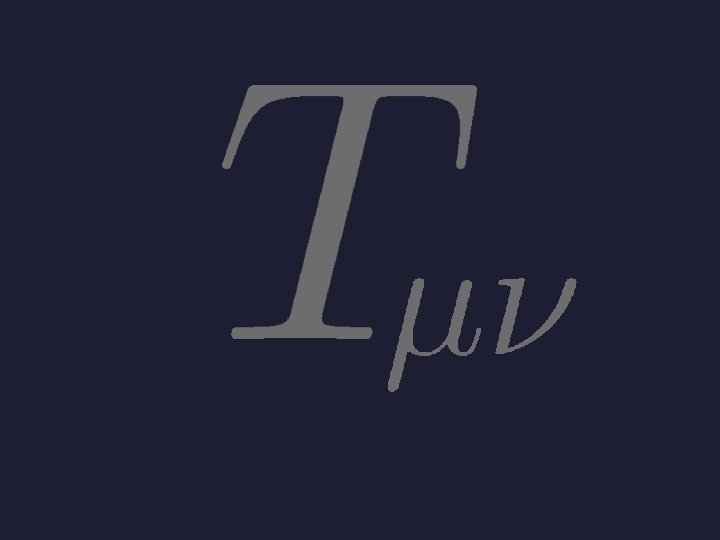
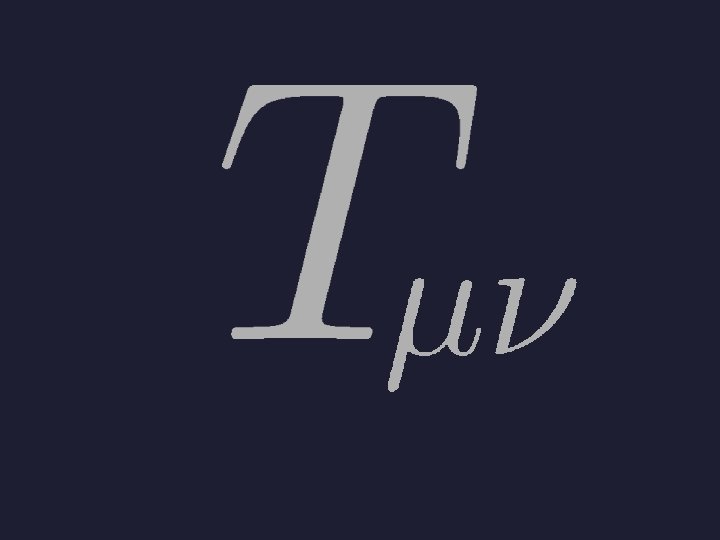


Poincare symmetry

energy momentum Poincare symmetry stress pressure

energy momentum Poincare symmetry stress Einstein Equation pressure Hydrodynamic Eq.

: nontrivial observable on the lattice Definition of the operator is nontrivial ①because of the explicit breaking of Lorentz symmetry ex: Its measurement is extremely noisy ②due to high dimensionality and etc.

If we have

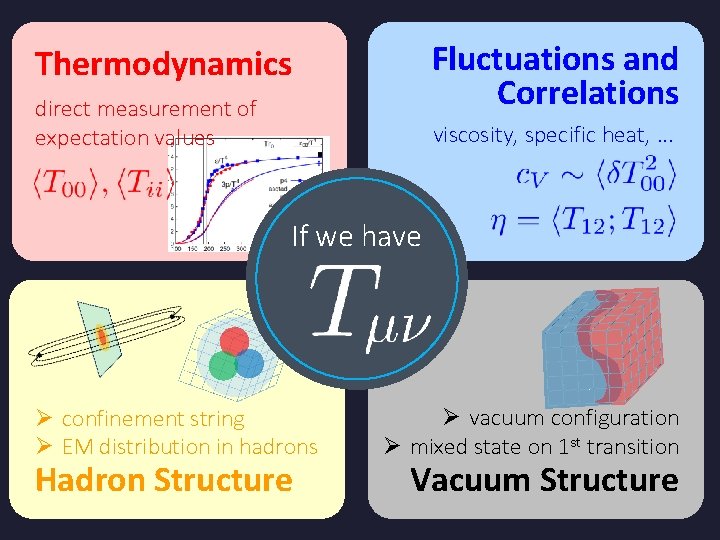
Thermodynamics direct measurement of expectation values If we have

Thermodynamics direct measurement of expectation values Fluctuations and Correlations viscosity, specific heat, . . . If we have

Fluctuations and Correlations Thermodynamics direct measurement of expectation values viscosity, specific heat, . . . If we have Ø confinement string Ø EM distribution in hadrons Hadron Structure Ø vacuum configuration Ø mixed state on 1 st transition Vacuum Structure

Measurement of Thermodynamics using gradient flow Masakiyo Kitazawa (Osaka U. ) for Flow. QCD Collaboration Asakawa, Hatsuda, Iritani, Itou, MK, Suzuki Flow. QCD, ar. Xiv: 1312. 7492[hep-lat]; to appear in PRD LATTICE 2014, 28 June 2014, New York

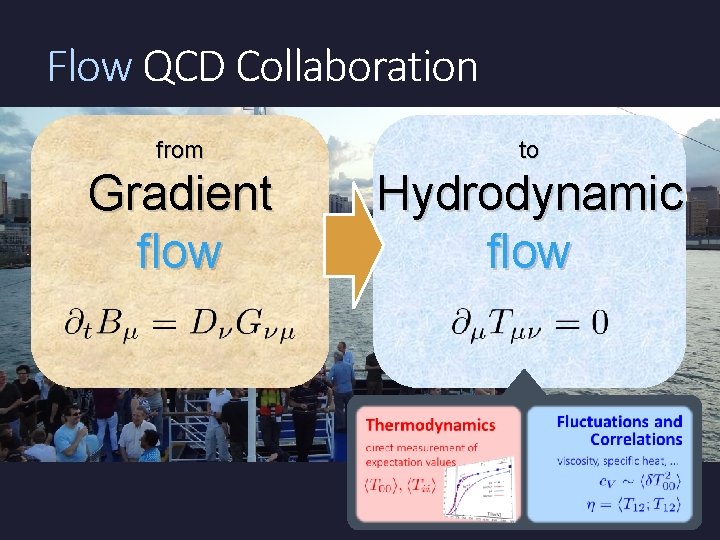
Flow QCD Collaboration

Flow QCD Collaboration from Gradient flow

Flow QCD Collaboration from to Gradient flow Hydrodynamic flow

Gradient Flow
![YM Gradient Flow t flow time dim length 2 Luescher 2010 A Ramos plenary YM Gradient Flow t: “flow time” dim: [length 2] Luescher, 2010 A. Ramos, plenary,](https://slidetodoc.com/presentation_image_h2/7b35ce797be5dc4dc33038533196ce27/image-19.jpg)
YM Gradient Flow t: “flow time” dim: [length 2] Luescher, 2010 A. Ramos, plenary, Friday

YM Gradient Flow Luescher, 2010 A. Ramos, plenary, Friday t: “flow time” dim: [length 2] p transform gauge field like diffusion equation p diffusion length p This is NOT the standard cooling/smearing p All composite operators at t>0 are UV finite Luescher, Weisz, 2011

Applications of Gradient Flow A. Ramos, plenary, Friday ① scale setting ② running coupling ③ topology ④ operator relation ⑤ autocorrelation, etc.

Small Flow Time Expansion of Operators and EMT

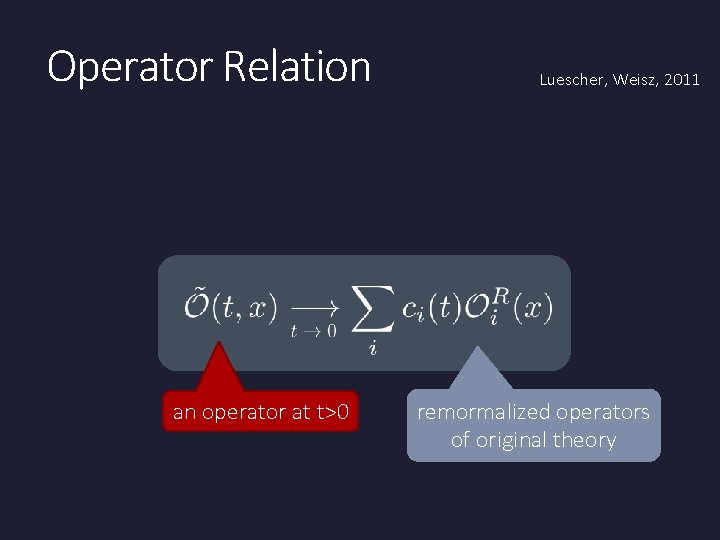
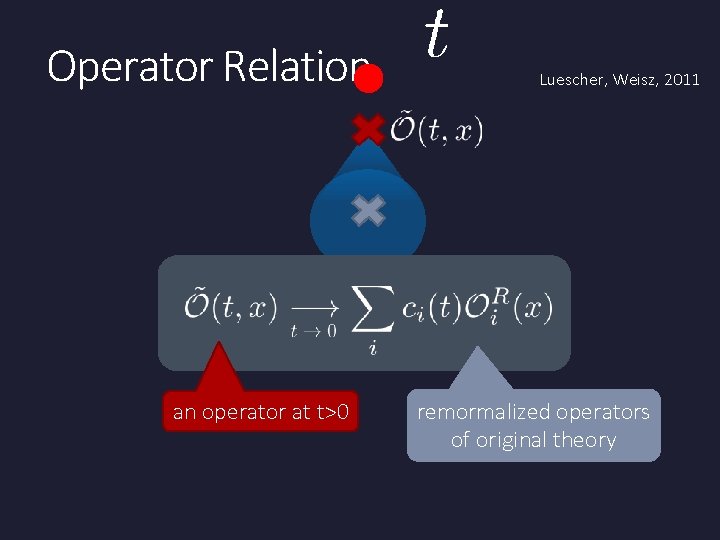
Operator Relation an operator at t>0 Luescher, Weisz, 2011 remormalized operators of original theory

Operator Relation an operator at t>0 Luescher, Weisz, 2011 remormalized operators of original theory

Operator Relation an operator at t>0 Luescher, Weisz, 2011 remormalized operators of original theory

Constructing EMT Suzuki, 2013 Del. Debbio, Patella, Rago, 2013 p gauge-invariant dimension 4 operators

Constructing EMT 2 Suzuki coeffs. See also, Patella, Parallel 7 E, Thu. Suzuki, 2013

Constructing EMT 2 Suzuki coeffs. Remormalized EMT Suzuki, 2013

Numerical Analysis on the Lattice

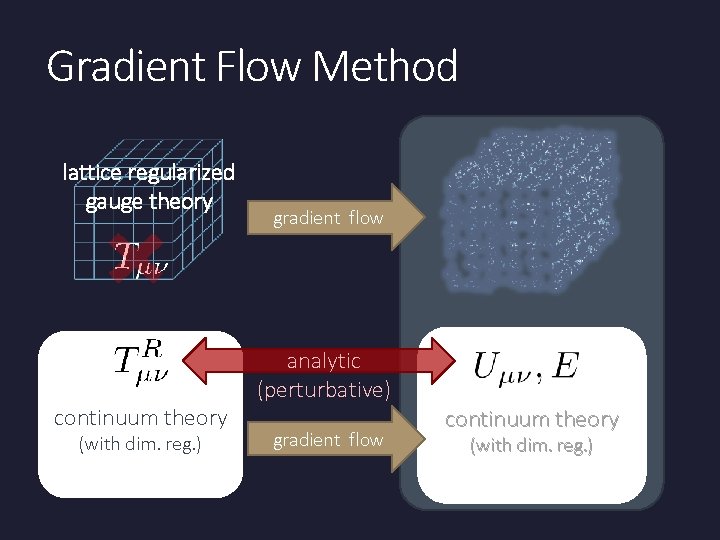
Gradient Flow Method lattice regularized gauge theory continuum theory (with dim. reg. ) gradient flow analytic (perturbative) gradient flow continuum theory (with dim. reg. )

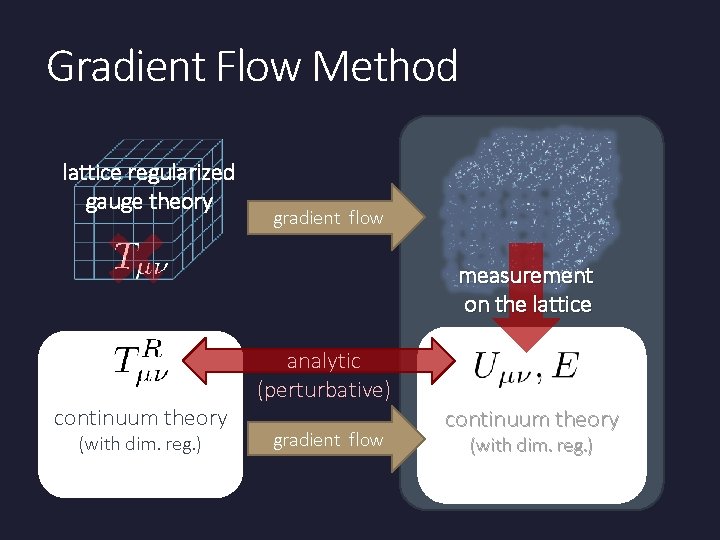
Gradient Flow Method lattice regularized gauge theory gradient flow measurement on the lattice continuum theory (with dim. reg. ) analytic (perturbative) gradient flow continuum theory (with dim. reg. )

Caveats Gauge field has to be sufficiently smeared! lattice regularized gauge theory Perturbative relation gradient flow has to be applicable! measurement on the lattice continuum theory (with dim. reg. ) analytic (perturbative) gradient flow continuum theory (with dim. reg. )

Caveats Gauge field has to be sufficiently smeared! lattice regularized gauge theory Perturbative relation gradient flow has to be applicable! continuum theory (with dim. reg. ) analytic (perturbative) gradient flow continuum theory (with dim. reg. )

in continuum non-perturbative region O(t) effect classical

in continuum non-perturbative region O(t) effect classical on the lattice p t 0 limit with keeping t>>a 2

Numerical Simulation Ø SU(3) YM theory Ø Wilson gauge action twice Simulation 2 Simulation 1 lattice size: 323 x. Nt Nt = 6, 8, 10 b = 5. 89 – 6. 56 ~300 configurations using SX 8 @ RCNP SR 16000 @ KEK attice! (new, preliminary) (ar. Xiv: 1312. 7492) • • finer l • • lattice size: 643 x. Nt Nt = 10, 12, 14, 16 b = 6. 4 – 7. 4 ~2000 configurations using Blue. Gene. Q @ KEK efficiency ~40%

Numerical Simulation Ø SU(3) YM theory Ø Wilson gauge action twice Simulation 2 Simulation 1 lattice size: 323 x. Nt Nt = 6, 8, 10 b = 5. 89 – 6. 56 ~300 configurations using SX 8 @ RCNP SR 16000 @ KEK attice! (new, preliminary) (ar. Xiv: 1312. 7492) • • finer l • • lattice size: 643 x. Nt Nt = 10, 12, 14, 16 b = 6. 4 – 7. 4 ~2000 configurations using Blue. Gene. Q @ KEK efficiency ~40%

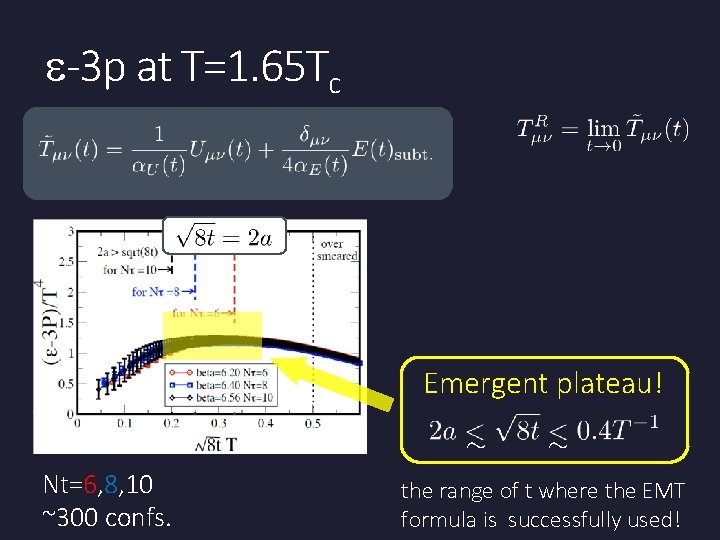
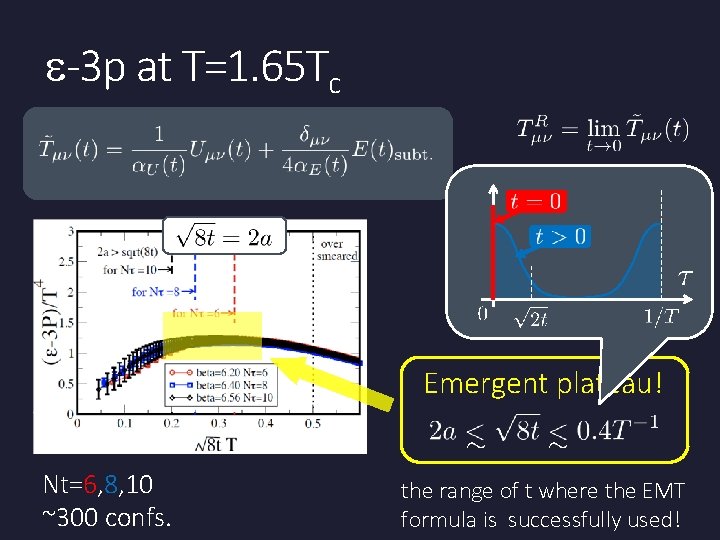
e-3 p at T=1. 65 Tc Emergent plateau! Nt=6, 8, 10 ~300 confs. the range of t where the EMT formula is successfully used!

e-3 p at T=1. 65 Tc Emergent plateau! Nt=6, 8, 10 ~300 confs. the range of t where the EMT formula is successfully used!

Entropy Density at T=1. 65 Tc Emergent plateau! systematic error Nt=6, 8, 10 ~300 confs. Direct measurement of e+p on a given T! NO integral / NO vacuum subtraction

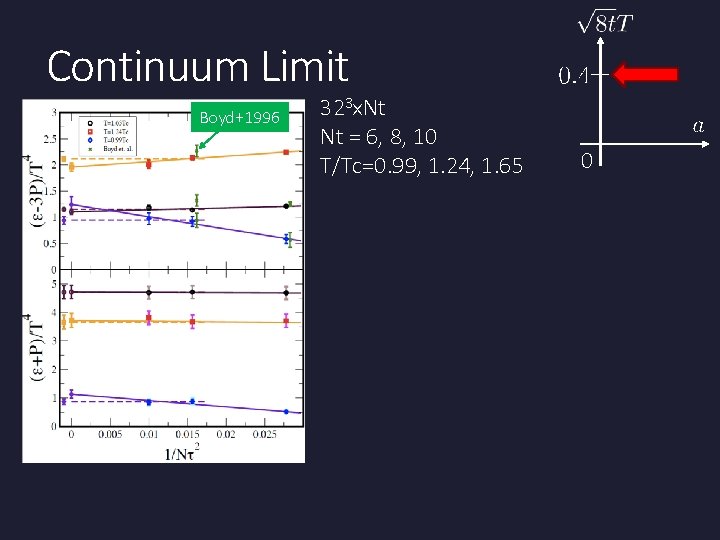
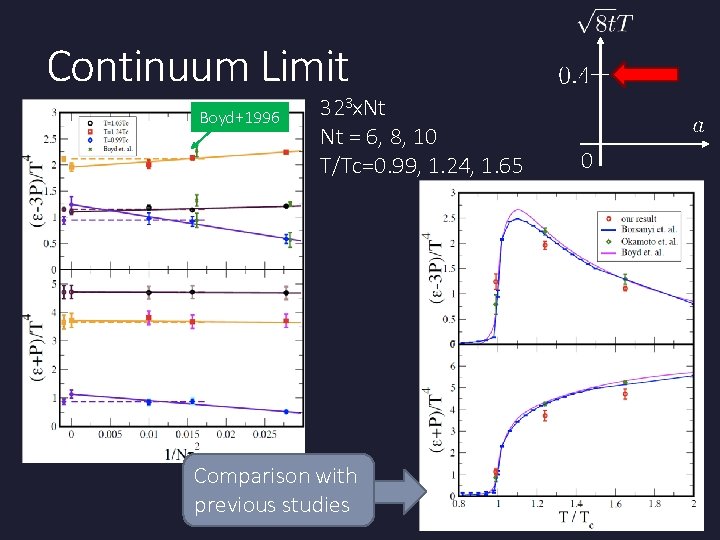
Continuum Limit Boyd+1996 323 x. Nt Nt = 6, 8, 10 T/Tc=0. 99, 1. 24, 1. 65 0

Continuum Limit Boyd+1996 323 x. Nt Nt = 6, 8, 10 T/Tc=0. 99, 1. 24, 1. 65 Comparison with previous studies 0

Numerical Simulation Ø SU(3) YM theory Ø Wilson gauge action twice Simulation 2 Simulation 1 lattice size: 323 x. Nt Nt = 6, 8, 10 b = 5. 89 – 6. 56 ~300 configurations using SX 8 @ RCNP SR 16000 @ KEK attice! (new, preliminary) (ar. Xiv: 1312. 7492) • • finer l • • lattice size: 643 x. Nt Nt = 10, 12, 14, 16 b = 6. 4 – 7. 4 ~2000 configurations using Blue. Gene. Q @ KEK efficiency ~40%

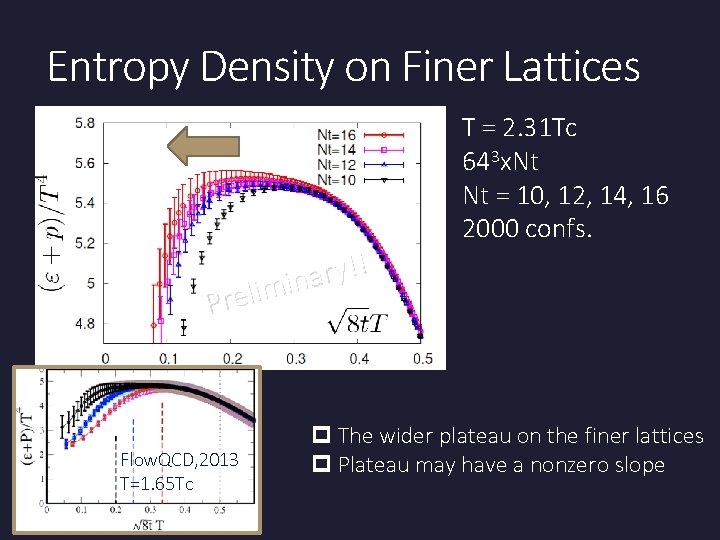
Entropy Density on Finer Lattices ! ! y r a n i m i l Pre Flow. QCD, 2013 T=1. 65 Tc T = 2. 31 Tc 643 x. Nt Nt = 10, 12, 14, 16 2000 confs. p The wider plateau on the finer lattices p Plateau may have a nonzero slope

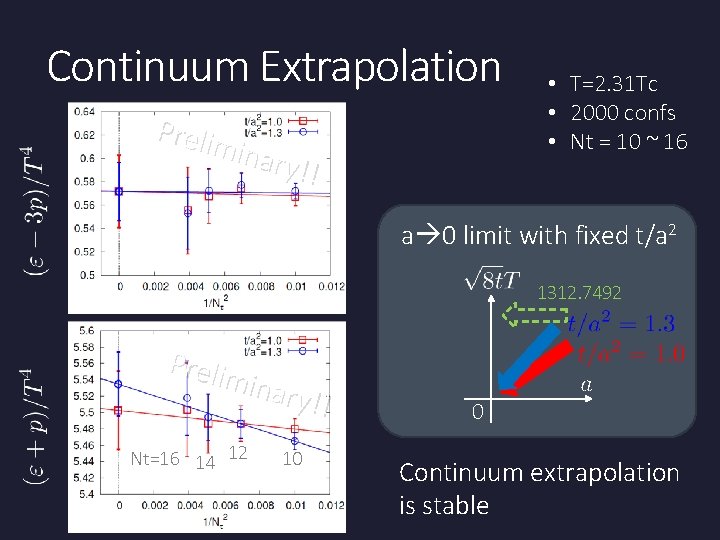
Continuum Extrapolation Prelim inary !! • T=2. 31 Tc • 2000 confs • Nt = 10 ~ 16 a 0 limit with fixed t/a 2 1312. 7492 Prelim inary !! Nt=16 14 12 10 0 Continuum extrapolation is stable

Summary

Summary EMT formula from gradient flow This formula can successfully define and calculate the EMT on the lattice This operator provides us with novel approaches to measure various observables on the lattice! This method is direct, intuitive and less noisy

Many F uture S tudies! ! Other observables O(a) improvement Nogradi, 7 E(Thu); Sint, 7 E(Thu) full QCD Makino, Suzuki, 2014 non-pert. improvement Patella 7 E(Thu) Monahan, 7 E(Thu) and etc.

One More Thing…

One More Thing… Fluctuations and Correlations viscosity, specific heat, . . .

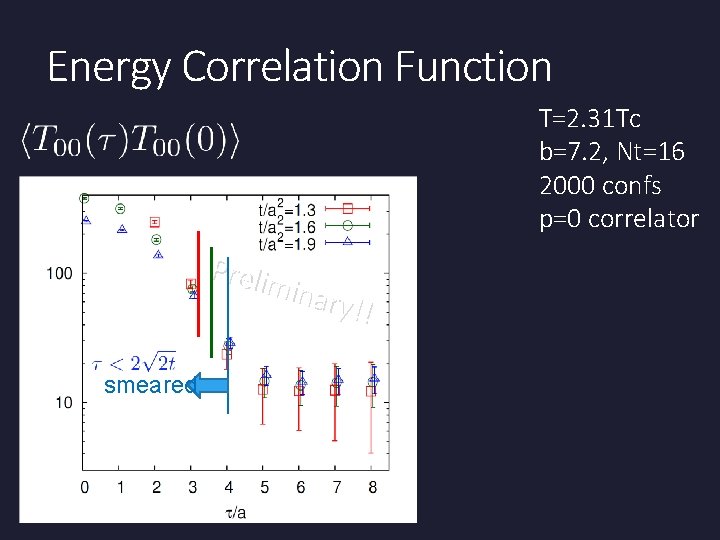
Energy Correlation Function T=2. 31 Tc b=7. 2, Nt=16 2000 confs p=0 correlator Prelim inary !! smeared

Energy Correlation Function T=2. 31 Tc b=7. 2, Nt=16 2000 confs p=0 correlator Prelim inary !! smeared p t independent const. energy conservation

Energy Correlation Function T=2. 31 Tc b=7. 2, Nt=16 2000 confs p=0 correlator Prelim inary !! smeared p t independent const. energy conservation p specific heat Novel approach to measure specific heat!

Keep your attention to this new flow just like…

Keep your attention to this new flow just like… Thank you for your attention!