Thermodynamics Multicomponent Homogeneous System Solution ByeongJoo Lee Thermodynamics

Thermodynamics Multi-component Homogeneous System: Solution Byeong-Joo Lee Thermodynamics POSTECH - MSE calphad@postech. ac. kr Byeong-Joo Lee http: //cmse. postech. ac. kr

Thermodynamic Properties of Gases - mixture of ideal gases 1 mole of ideal gas @ constant T: Mixture of Ideal Gases Definition of Mole fraction: xi Definition of partial pressure: pi Partial molar quantities: Byeong-Joo Lee http: //cmse. postech. ac. kr

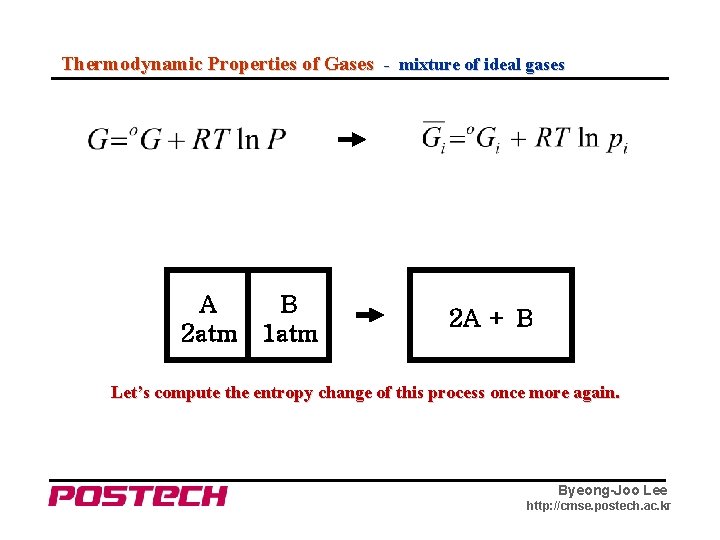
Thermodynamic Properties of Gases - mixture of ideal gases A 2 atm B 1 atm 2 A + B Let’s compute the entropy change of this process once more again. Byeong-Joo Lee http: //cmse. postech. ac. kr

Thermodynamic Properties of Gases - mixture of ideal gases Heat of Mixing of Ideal Gases Gibbs Free Energy of Mixing of Ideal Gases when pressure is always 1 atm Entropy of Mixing of Ideal Gases Byeong-Joo Lee http: //cmse. postech. ac. kr

Thermodynamic Properties of Gases - Treatment of nonideal gases Introduction of fugacity, f as For Equation of state ※ actual pressure of the gas is the geometric mean of the fugacity and the ideal P ※ The percentage error involved in assuming the fugacity to be equal to the pressure is the same as the percentage departure from the ideal gas law Byeong-Joo Lee http: //cmse. postech. ac. kr

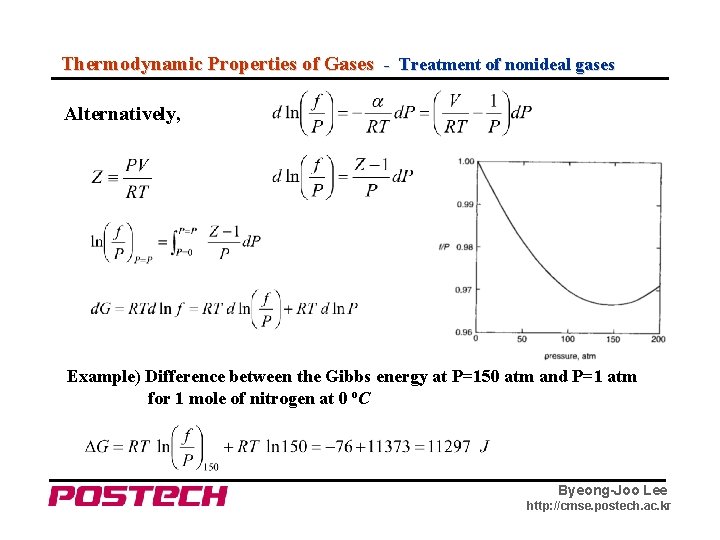
Thermodynamic Properties of Gases - Treatment of nonideal gases Alternatively, Example) Difference between the Gibbs energy at P=150 atm and P=1 atm for 1 mole of nitrogen at 0 o. C Byeong-Joo Lee http: //cmse. postech. ac. kr

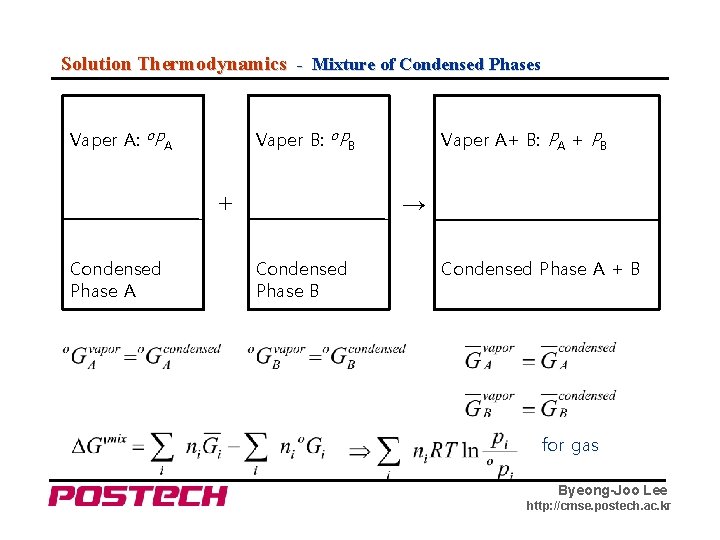
Solution Thermodynamics - Mixture of Condensed Phases Vaper A: o. PA Vaper B: o. PB + Condensed Phase A Vaper A+ B: PA + PB → Condensed Phase B Condensed Phase A + B for gas Byeong-Joo Lee http: //cmse. postech. ac. kr

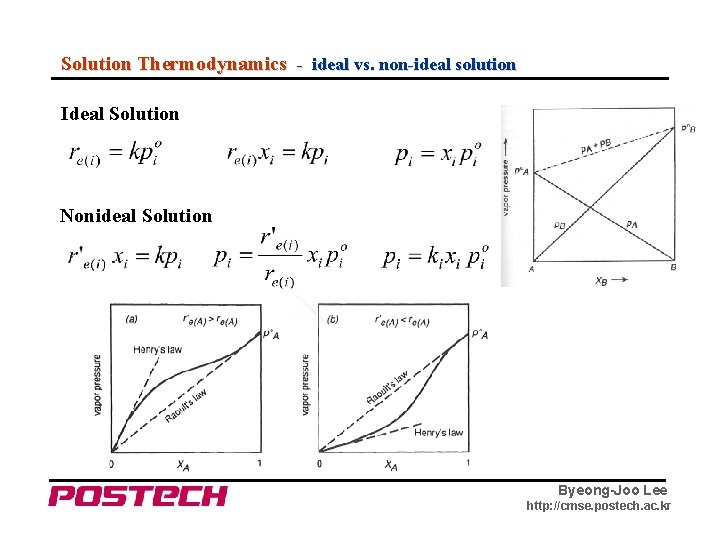
Solution Thermodynamics - ideal vs. non-ideal solution Ideal Solution Nonideal Solution Byeong-Joo Lee http: //cmse. postech. ac. kr

Solution Thermodynamics - Thermodynamic Activity of a Component in Solution → for ideal solution Draw a composition-activity curve for an ideal and nonideal solution Henrian vs. Raoultian Byeong-Joo Lee http: //cmse. postech. ac. kr

Solution Thermodynamics - Partial Molar Property ▷ Partial Molar Quantity ▷ Molar Properties of Mixture Gibbs-Duhem Equation Byeong-Joo Lee http: //cmse. postech. ac. kr

Solution Thermodynamics - Partial Molar Quantity of Mixing definition of solution and mechanical mixing where is a pure state value per mole 왜 partial molar quantity를 사용해야 하는가? Byeong-Joo Lee http: //cmse. postech. ac. kr

Solution Thermodynamics - Partial Molar Quantities Byeong-Joo Lee http: //cmse. postech. ac. kr

Solution Thermodynamics - Partial Molar Quantities Evaluation of Partial Molar Properties in 1 -2 Binary System • Partial Molar Properties from Total Properties example) • Partial molar & Molar Gibbs energy of mixing vs. Gibbs energy of formation • Graphical Determination of Partial Molar Properties: Tangential Intercepts • Evaluation of a PMP of one component from measured values of a PMP of the other example) Byeong-Joo Lee http: //cmse. postech. ac. kr

Solution Thermodynamics - Chemical Potential as a Partial Molar Quantity ※ Relationships among Partial Molar Quantities: Chapter 5에서 언급한 Thermodynamic Relationship 들이 모두 적용됨 Byeong-Joo Lee http: //cmse. postech. ac. kr

Solution Thermodynamics - Non-Ideal Solution ▷ Activity Coefficient ▷ Behavior of Dilute Solutions Byeong-Joo Lee http: //cmse. postech. ac. kr

Example 1. Gibbs energy of formation과 Gibbs energy of mixing의 차이는 무엇인가? 2. Solution에서 한 성분이 Henrian 또는 Raoultian 거동을 한다는 것을 무엇을 의미하는가? Molar Gibbs energy가 다음과 같이 표현되는 A-B 2원 Solution phase에서 각 성분은 dilute 영역에서는 Henrian 거동을, rich 영역에서는 Raoultian 거동을 보인다는 것을 증명하시오. Byeong-Joo Lee http: //cmse. postech. ac. kr

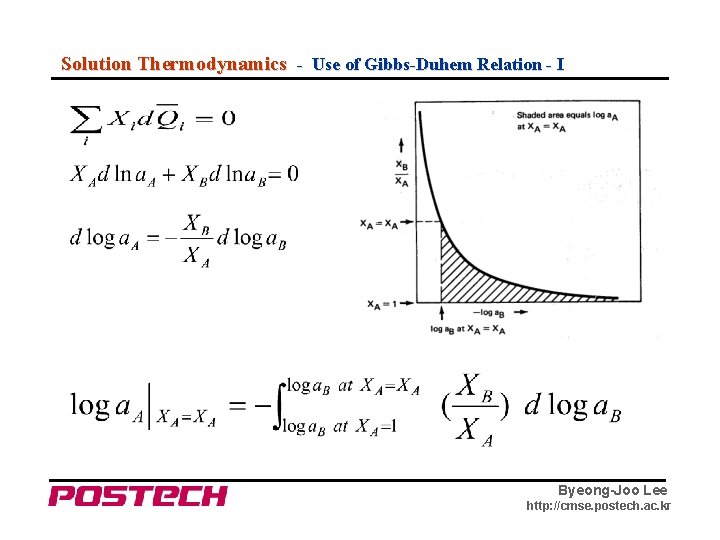
Solution Thermodynamics - Use of Gibbs-Duhem Relation - I Byeong-Joo Lee http: //cmse. postech. ac. kr

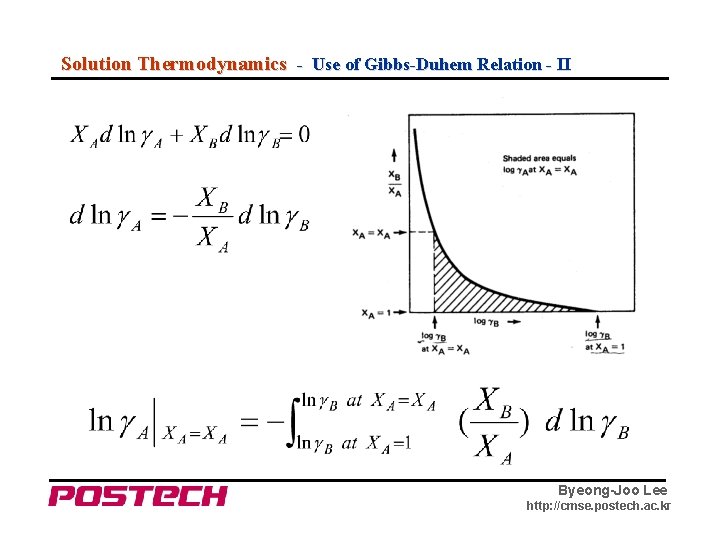
Solution Thermodynamics - Use of Gibbs-Duhem Relation - II Byeong-Joo Lee http: //cmse. postech. ac. kr

Solution Thermodynamics - Introduction of α-function Byeong-Joo Lee http: //cmse. postech. ac. kr

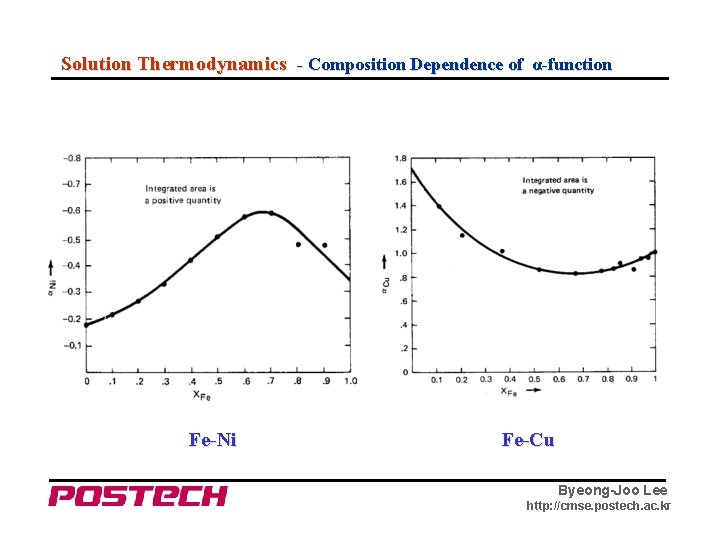
Solution Thermodynamics - Composition Dependence of α-function Fe-Ni Fe-Cu Byeong-Joo Lee http: //cmse. postech. ac. kr

Solution Thermodynamics - Regular Solution Model • Margules, 1895. • Hildebrand, 1929. (using van Laar Equation) Byeong-Joo Lee http: //cmse. postech. ac. kr

Solution Thermodynamics - Quasi-Chemical Model, Guggenheim, 1935. Byeong-Joo Lee http: //cmse. postech. ac. kr

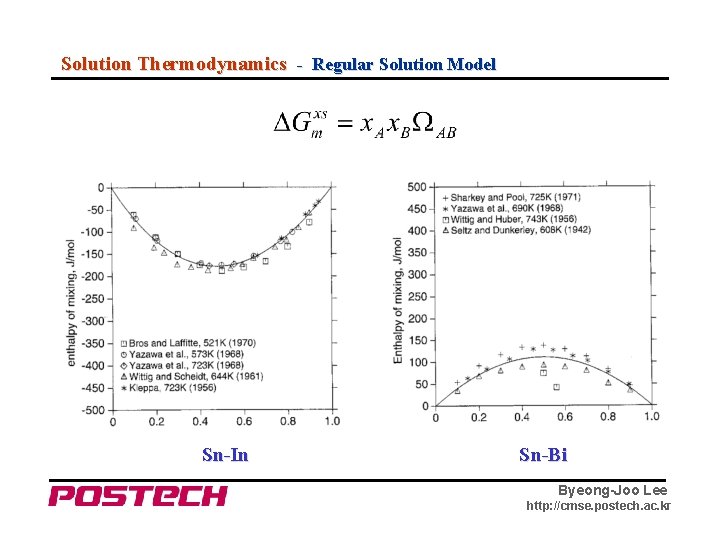
Solution Thermodynamics - Regular Solution Model Sn-In Sn-Bi Byeong-Joo Lee http: //cmse. postech. ac. kr

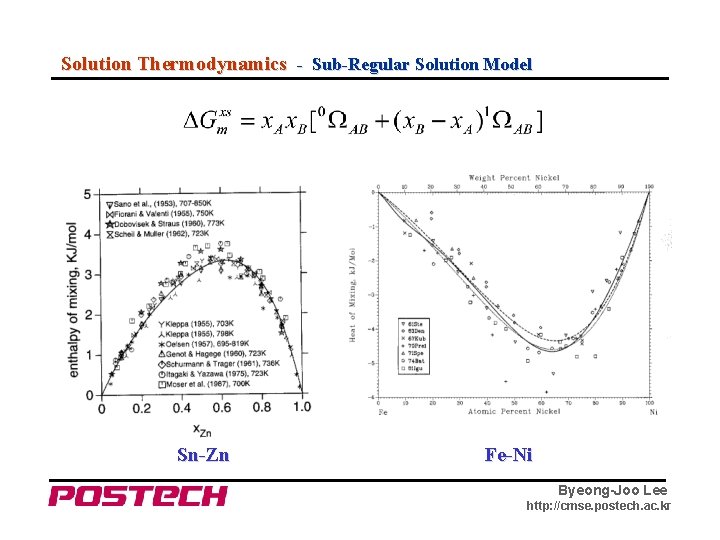
Solution Thermodynamics - Sub-Regular Solution Model Sn-Zn Fe-Ni Byeong-Joo Lee http: //cmse. postech. ac. kr

Solution Thermodynamics - Regular Solution Model • Composition and temperature dependence of Ω • Extension into ternary and multi-component system • Sublattice Model • Inherent Inconsistency Byeong-Joo Lee http: //cmse. postech. ac. kr