Thermodynamics AP Chemistry System Surroundings and Universe System










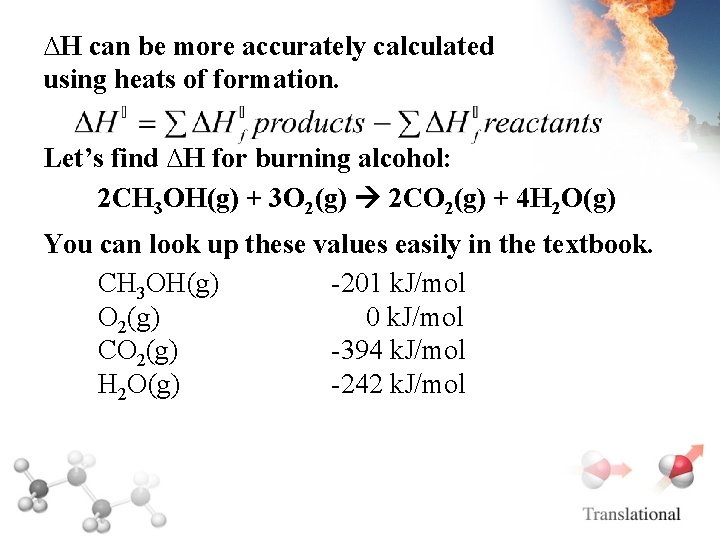














- Slides: 33

Thermodynamics AP Chemistry

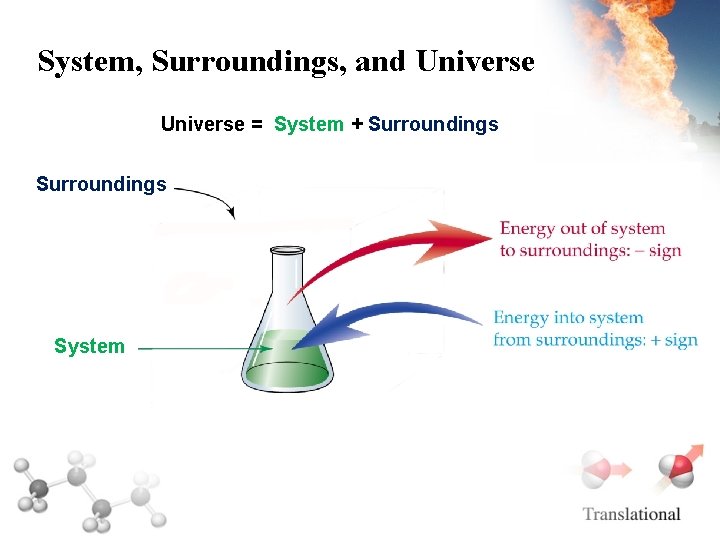
System, Surroundings, and Universe = System + Surroundings System

The 1 st law of thermodynamics: “Energy is neither created nor destroyed” The total change in internal energy = Heat lost or gained + U = q + Work done on or by a system w

Within the scope of this course, we are concerned with HEAT (q). U = q + w Heat lost or gained At a constant pressure, (a reasonable assumption for problems in this course) q = H

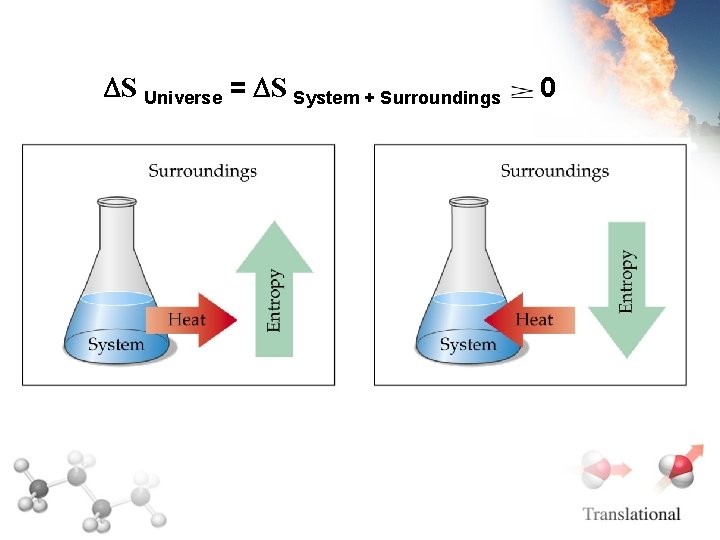
The 2 nd law of thermodynamics: In any isolated system entropy will always increase or stay the same. The entropy of the universe, an isolated system (system + surroundings) will always increase or stay the same. Change in Entropy = S

S Universe = S System + Surroundings 0

There are 3 State Functions we will look at: 1. ∆H = a change in enthalpy (heat) 2. ∆S = a change in entropy (disorder) 3. ∆G = Gibbs free energy (spontaneity) State functions depend only on the change before and after a reaction occurs, not how it occurs. For example, a catalyst will not change any of these values for a reaction.

There are 3 State Functions we will look at: You might see the little circle ∆H°. This just means the state function value is calculated at “Standard State Conditions, STP ” Gases are at 1 atm & 25°C (room temperature) Liquids & solids are pure Solutions are 1 M concentration Energy of formation of pure elements is zero

Enthalpy Change, or ∆H (or change in heat) Chemical reactions may release or absorb heat. When bonds are formed, energy is released. In order to break bonds, energy must be absorbed. Strong bonds ≅ more stability ≅ lower enthalpy Weaker bonds ≅ less stability ≅ higher enthalpy Bond Energy: The energy it takes to break a bond.

Enthalpy Change, or ∆H (or change in heat) ∆H can be roughly approximated* from bond energies. Breaking a bond always takes energy, so these values are positive. When a new bond is formed, energy equal to the bond energy is released. (lower energy state, more stable) * Bond energy calculations are not prefect as they exclude many important factors, such as changes in phase. Enthalpy is best calculated by examining heats of formation.

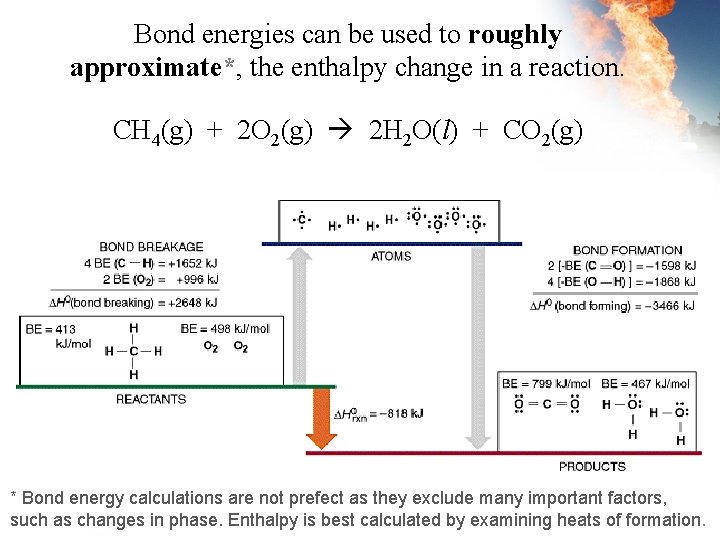
Enthalpy Change, or ∆H (or change in heat) Find ∆H for: CH 4(g) + 2 O 2(g) 2 H 2 O(l) + CO 2(g) From a chart in the text (pg. 351) you could find: C=C 614 k. J/mol O=O 498 k. J/mol C=O 754 k. J/mol O–H 467 k. J/mol C–H 413 k. J/mol C=O 799 k. J/mol (in CO 2) * Bond energy calculations are not prefect as they exclude many important factors, such as changes in phase. Enthalpy is best calculated by examining heats of formation.

Bond energies can be used to roughly approximate*, the enthalpy change in a reaction. CH 4(g) + 2 O 2(g) 2 H 2 O(l) + CO 2(g) * Bond energy calculations are not prefect as they exclude many important factors, such as changes in phase. Enthalpy is best calculated by examining heats of formation.

Exothermic Reactions: • Reactants had weaker bonds, • Less stable, • More enthalpy than products, so some heat was released. • ∆H is a negative value. Most reactions are Exothermic because the universe favors systems with low energy states because they’re more stable. Endothermic Reactions: Just the opposite from above. Energy must be added for the reaction to occur.

∆H can be more accurately calculated using heats of formation: Heats of Formation, Hof This is how much energy it takes to form the chemical from pure elements. If Hof is negative, energy was released to make the compound, it’s more stable, and it was exothermic. If Hof is positive, it’s unstable and it was endothermic, or energy was absorbed to make it.
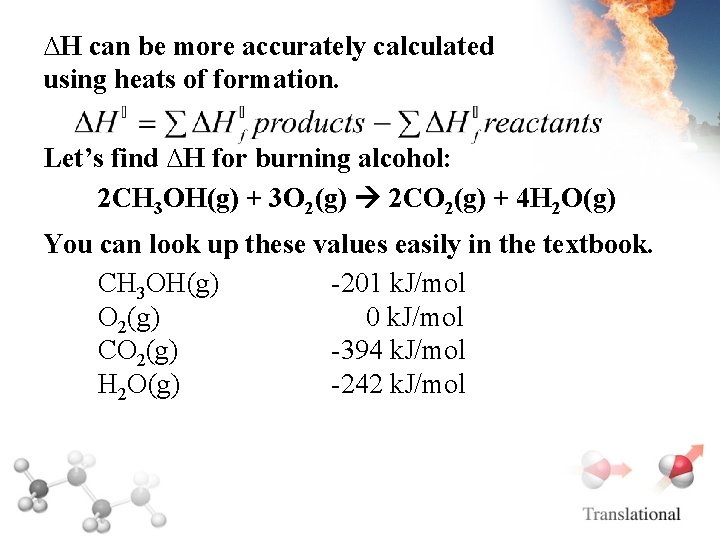
∆H can be more accurately calculated using heats of formation. Let’s find ∆H for burning alcohol: 2 CH 3 OH(g) + 3 O 2(g) 2 CO 2(g) + 4 H 2 O(g) You can look up these values easily in the textbook. CH 3 OH(g) -201 k. J/mol O 2(g) 0 k. J/mol CO 2(g) -394 k. J/mol H 2 O(g) -242 k. J/mol

2 CH 3 OH(g) + 3 O 2(g) 2 CO 2(g) + 4 H 2 O(g) ∆H = [(2)(-394 k. J)+(4)(-242 k. J)] - [(2)(-201 k. J)+0] ∆H = -1354 k. J (note: for two moles of alcohol) For the ∆H of alcohol (per mole), divide this by two. Tie it into stoichiometry! 2 mols CH 3 OH(g) ≅ 3 mols O 2(g) ≅ -1354 k. J ≅ etc…

AP Exam Multiple Choice Question 2002, #25. ( 66% of students got this correct) 3 C 2 H 2(g) C 6 H 6(g) What is the standard enthalpy change, ∆H˚, for the reaction represented above? (∆H˚f of C 2 H 2(g) is 230 k. J mol-1; ∆H˚f of C 6 H 6(g) is 83 k. J mol-1. ) (A) – 607 k. J (B) – 147 k. J (D) +19 k. J (E) +773 k. J (C) – 19 k. J

Hess’s Law: If a reaction takes place in several steps, the ∆H for the overall reaction is just the sum of the ∆H’s for each individual step. A note on enthalpy units: Hof refers to the standard enthalpy of formation and always has units of k. J per one mole of product (k. J/mol). In other cases (not heats of formation), following a reaction, you might see H listed with units of only k. J. In this case H is being viewed as an extensive property. You might also see H listed as an intensive property with units of k. J/mol or, more appropriately, k. J/molrxn – Seen on the 2007 AP Chemistry Exam. Both conventions will be used in this course to increase your exposure. The practical steps in solving problems will not change. Do not let the units throw you off.

Calorimetry Heat Capacity: does not include mass. Specific Heat: cp* is the heat needed to raise the temperature of one gram of material 1°C. Water has high cp, so lots of heat = little temp change Metals have low cp, so a little heat = very hot metal *Cp or cp implies that this is true at a constant pressure.

Remember calorimeters & the heat equation? q = m cp T * q = H = m cp T ** This is a great way to measure heat from reactions: The heat lost by the reaction goes into the water in the calorimeter and you can calculate the reaction heat, q. *assumes no phase change ** assumes no phase change and constant pressure

Entropy Change, or ∆S Entropy: This is a measure of the disorder of a system. The more disorder, the bigger the value of S, entropy. * * Technically, entropy can only be roughly analogized to “disorder” and neither entropy nor trends in the universe can be attributed directly to a system’s change in “disorder. ” Strictly speaking, “entropy is the measure of energy dispersal, as a function of temperature. ” Nevertheless, the “disorder” analogy is useful and acceptable within the scope of this chemistry course.

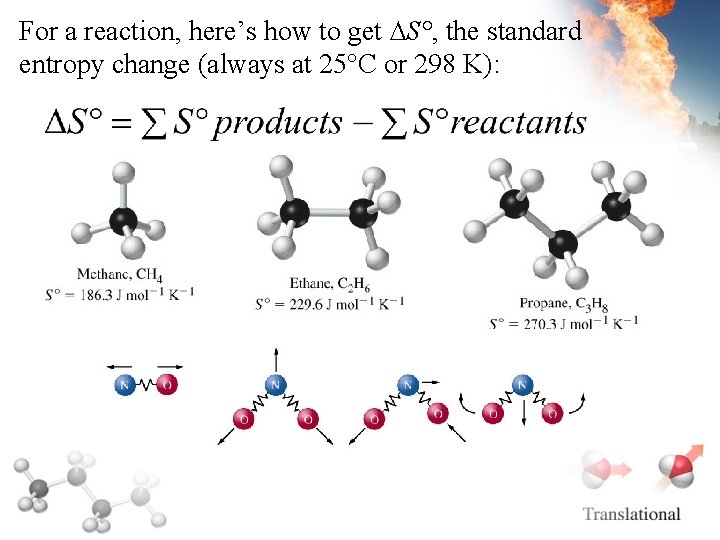
Entropy Change, or ∆S 0 entropy is defined as the entropy in a solid crystal at 0 K, so all things have a positive value for entropy. Liquids have higher S than solids Gases have a higher S than liquids Aqueous particles have more S than solids 3 moles of a substance has more S than one mole

For a reaction, here’s how to get ∆S°, the standard entropy change (always at 25°C or 298 K):

Gibb’s Free Energy, or ∆G Can be thought of as a measure of the work available from, or necessary for, a chemical reaction. If ∆G is negative, energy is released, work is available, and the reaction (rxn) is spontaneous! If ∆G is positive, energy is required, work is necessary, and the reverse reaction (rxn) is spontaneous.

Consider the electrolysis of water: H 2 O H 2 + ½ O 2 ΔH = 285. 83 k. J Do you need to supply that much energy from the battery? Why or why not? No! The entropy increases in the process of dissociation, and the amount TΔS can be provided from the environment at temperature T. ΔH = 285. 83 k. J H 2 O H 2 + ½ O 2 ΔS = 163 J ΔG = ΔH - TΔS = 285. 83 k. J – (0. 163 k. J)(298 K) = 237. 1 k. J (is needed) Look out for entropy units with ΔG calculations

Consider the electrolysis of water: H 2 O H 2 + ½ O 2 ΔG = + The amount you need to supply is ΔG, Gibbs free energy! Work is required, ΔG is +, and the process is not spontaneous. However, the reverse process is spontaneous and ΔG is –. H 2 + ½ O 2 H 2 O ΔG = – You know this is spontaneous if you’ve ever ignited hydrogen gas.

Gibb’s Free Energy, or ∆G Nature loves systems with low energy & high disorder! So nature likes systems with decreasing enthalpy ∆H (heat lost; ∆H = ─) and increasing entropy ∆S. Carefully look at what’s happening in a rxn to see if it’s going to be spontaneous. At low Temps, enthalpy dominates, but at high Temps, entropy is dominant - look at equation to see this. .

Gibb’s Free Energy, or ∆G Summary of Gibbs law for spontaneity: H S Result - + spontaneous at all temps + + spontaneous at high temps - - spontaneous at low temps + - not spontaneous at any temp

Gibb’s Free Energy, or ∆G Here’s how to get a Gibbs value, ∆G, for a reaction: ∆Gof is the standard free energy of formation. Note: ∆Hof = 0 ∆Gof = 0 ∆Sof ≠ 0

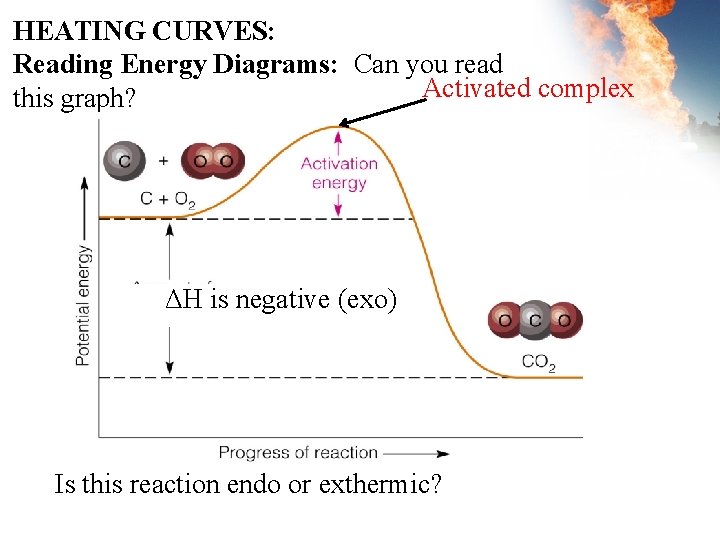
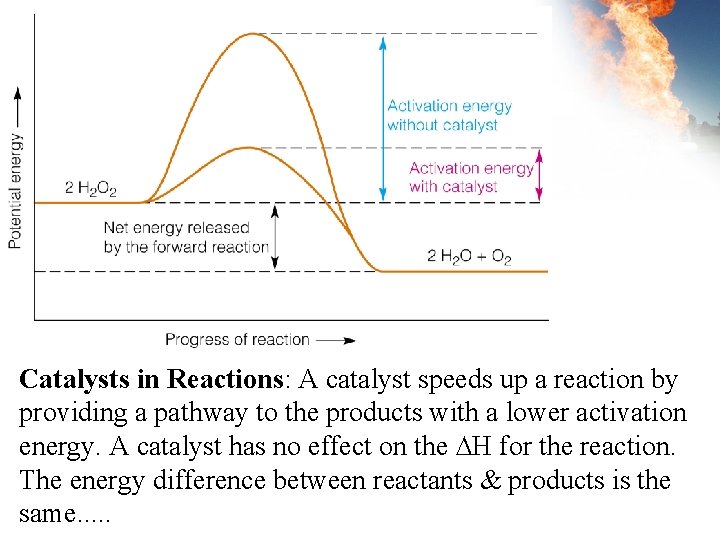
HEATING CURVES: Reading Energy Diagrams: Can you read Activated complex this graph? ΔH is negative (exo) Is this reaction endo or exthermic?

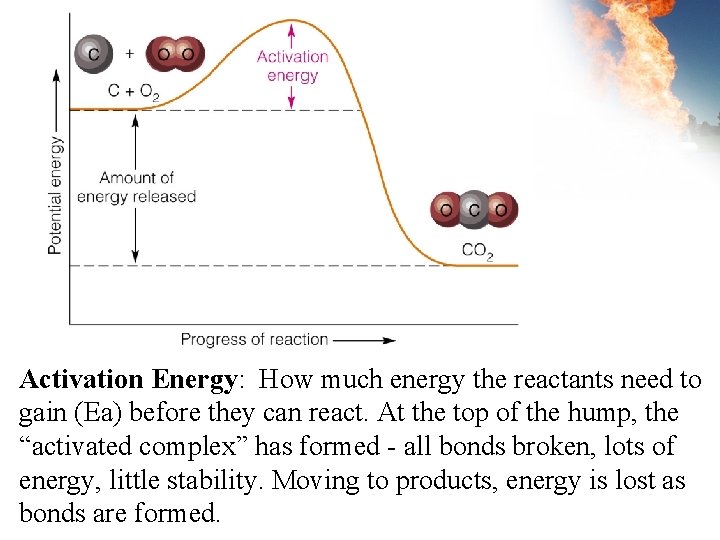
Activation Energy: How much energy the reactants need to gain (Ea) before they can react. At the top of the hump, the “activated complex” has formed - all bonds broken, lots of energy, little stability. Moving to products, energy is lost as bonds are formed.

Catalysts in Reactions: A catalyst speeds up a reaction by providing a pathway to the products with a lower activation energy. A catalyst has no effect on the ∆H for the reaction. The energy difference between reactants & products is the same. . .

Homework: Read 6. 1 -6. 3 (Enthalpy, Entropy & Specific Heat) Questions: #31, 33, 35, 37, #29, 41, 45, 49, 55 Read: 6. 3 -6. 4( Hess’s Law) Questions: # 57, 59, 61, 63, 65, 67, 71 Ch. 10 Questions: # 87, 89