Thermodynamics and Statistical Mechanics Heat Capacities Thermo Stat























- Slides: 26

Thermodynamics and Statistical Mechanics Heat Capacities Thermo & Stat Mech Spring 2006 Class 20 1

Diatomic Gas A gas of diatomic molecules can have translational, rotational and vibrational energy. Because of the spacing of the energy levels of each type of motion, they are not all equally excited. This shows up in the heat capacity. Thermo & Stat Mech - Spring 2006 Class 20 2

Partition Function For one molecule, e = etrans + erot + evib Thermo & Stat Mech - Spring 2006 Class 20 3

Partition Function Thermo & Stat Mech - Spring 2006 Class 20 4

Translational Motion Thermo & Stat Mech - Spring 2006 Class 20 5

Vibrational Motion Thermo & Stat Mech - Spring 2006 Class 20 6

High and Low Temperature Limits Thermo & Stat Mech - Spring 2006 Class 20 7

Rotational Motion Thermo & Stat Mech - Spring 2006 Class 20 8

Rotational Motion Thermo & Stat Mech - Spring 2006 Class 20 9

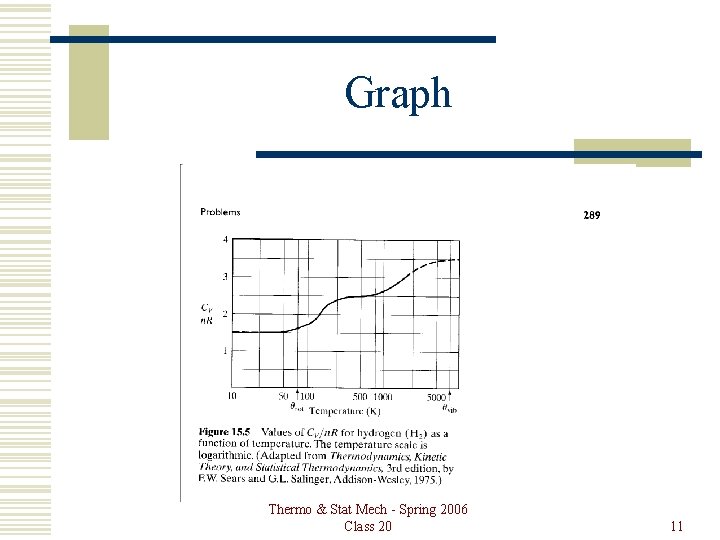
Diatomic Gas Overall Thermo & Stat Mech - Spring 2006 Class 20 10

Graph Thermo & Stat Mech - Spring 2006 Class 20 11

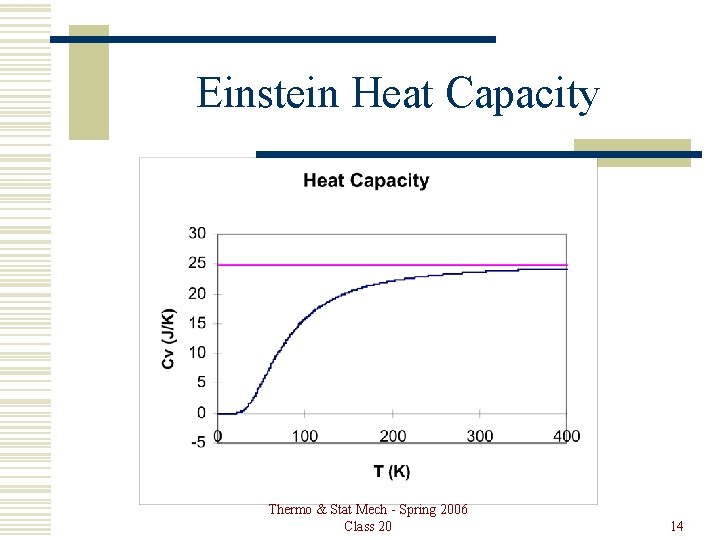
Einstein Solid Thermo & Stat Mech - Spring 2006 Class 20 12

Einstein Temperature Thermo & Stat Mech - Spring 2006 Class 20 13

Einstein Heat Capacity Thermo & Stat Mech - Spring 2006 Class 20 14

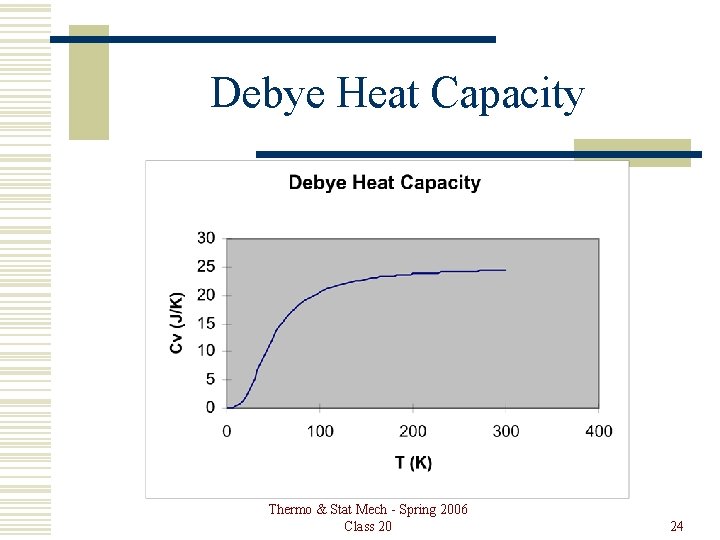
Debye Model of Solid The solid is treated as a continuum, calculating the number of standing wave states in the frequency range between w and w + d w, and Bose-Einstein statistics is used to determine the number of phonons in each state. Then the energy can be calculated. Thermo & Stat Mech - Spring 2006 Class 20 15

Density of States (Lec 17) Thermo & Stat Mech - Spring 2006 Class 20 16

Transverse and Longitudinal Thermo & Stat Mech - Spring 2006 Class 20 17

Density of States Thermo & Stat Mech - Spring 2006 Class 20 18

Phonon Energy Thermo & Stat Mech - Spring 2006 Class 20 19

Debye Cutoff Thermo & Stat Mech - Spring 2006 Class 20 20

Debye Temperature Thermo & Stat Mech - Spring 2006 Class 20 21

Energy Thermo & Stat Mech - Spring 2006 Class 20 22

Heat Capacity Thermo & Stat Mech - Spring 2006 Class 20 23

Debye Heat Capacity Thermo & Stat Mech - Spring 2006 Class 20 24

High Temperature Thermo & Stat Mech - Spring 2006 Class 20 25

Low Temperature Thermo & Stat Mech - Spring 2006 Class 20 26