Thermal Physics Thermodynamics and Temperature Thermodynamics deals with

Thermal Physics

Thermodynamics and Temperature • Thermodynamics deals with the internal energy of systems, and the key physical quantities in this context are: ØTemperature ØHeat ØEntropy ØInternal energy It is temperature that is most fundamental to quantifying thermal state of a system and the scale of measurement humans can best relate to in terms of defining “hot” and “cold”. • Absolute zero: the temperature of a body can be raised without limit, but it cannot be lowered without limit. If the pressure of a gas is kept constant, its volume is found to decrease linearly with temperature. Extrapolation shows that zero volume is reached at a temperature of -273. 15°C. Similarly if the volume of gas is kept constant, the pressure is seen to cross the zero -pressure axis at -273. 15°C. This temperature is known as absolute zero and is used to define the Kelvin scale: Tk=Tc + 273. 15.

• In practice, absolute zero can never be reached, with the lowest temperature being achieved in the laboratory being 2 x 10 -9 K. The Zeroth Law of Thermodynamics • Many bodies are said to be thermometric in their behaviour, since their properties change in response to changes in temperature. Examples are: ØVolume of liquid increases with increasing temperature ØMetal rod expands with increasing temperature ØElectrical resistance of a wire increases with increasing temperature This behaviour can be used as the basis of an instrument that measures temperature (i. e. , a thermometer). But how do we deal with the situation when we are trying to measure the temperature of one body which has a different temperature to the body we are trying to measure it with? This is where the zeroth law and the concept of thermal equilibrium are important.

The Zeroth Law of Thermodynamics contd. . . • In formal language the zeroth law states: “If two bodies are each in thermal equilibrium with a third body, then they are in thermal equilibrium with each other. ” • In plain language the zeroth law states: “Every body has a property called temperature. When two bodies are found to be in thermal equilibrium, their temperatures are equal. ” • How do we use this in an everyday situation? If we want to know whether the liquids in two different containers are at the same temperature, we measure each with a thermometer. We do not need to bring the two liquids into contact and observe whether or not they are in thermal equilibrium, since the zeroth law tells us they will be if at the same temperature.

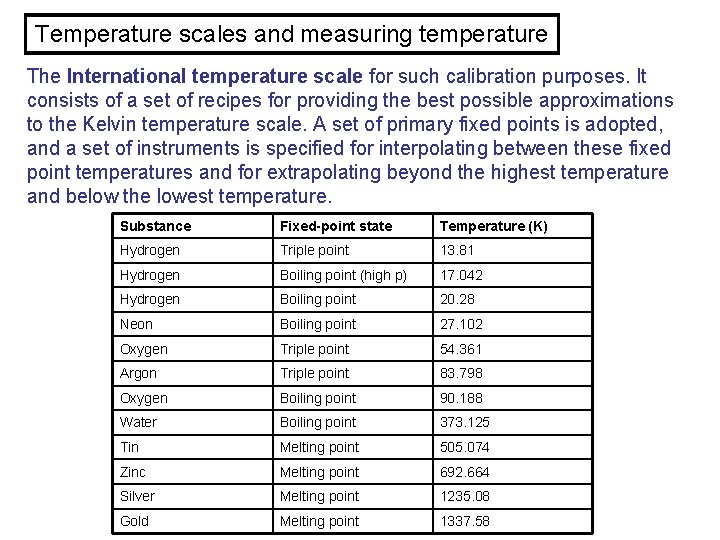
Temperature scales and measuring temperature Having established how we can measure temperatures, we now need to define a reproducible temperature scale in order that thermometers can be calibrated. The triple point of water: this is used to define a standard fixed point, since liquid water, solid ice, and water vapor can coexist in thermal equilibrium at only one set of temperature and pressure values. By international agreement (in 1967), the triple point of water has been assigned a value of 273. 16 K, and is denoted T 3. The constant volume gas thermometer: this has been adopted as the standard against which all othermometers are to be calibrated, and is based on the pressure exerted by a gas confined to a fixed volume. The international temperature scale: measuring temperatures precisely with a constant volume gas thermometer is arduous work, and so in practice, this thermometer is used only to establish certain “primary” fixed temperature points. These points can then be used to calibrate othermometers, such as the every-day mercury in glass thermometer.

Temperature scales and measuring temperature The International temperature scale for such calibration purposes. It consists of a set of recipes for providing the best possible approximations to the Kelvin temperature scale. A set of primary fixed points is adopted, and a set of instruments is specified for interpolating between these fixed point temperatures and for extrapolating beyond the highest temperature and below the lowest temperature. Substance Fixed-point state Temperature (K) Hydrogen Triple point 13. 81 Hydrogen Boiling point (high p) 17. 042 Hydrogen Boiling point 20. 28 Neon Boiling point 27. 102 Oxygen Triple point 54. 361 Argon Triple point 83. 798 Oxygen Boiling point 90. 188 Water Boiling point 373. 125 Tin Melting point 505. 074 Zinc Melting point 692. 664 Silver Melting point 1235. 08 Gold Melting point 1337. 58

Temperature scales and measuring temperature The Celsius and Fahrenheit Scales – the relationship between these two scales is: TF = 9/5 TC + 32° Thermal Expansion Most materials expand when heated. Over a limited range of temperatures, it is found that the linear expansion of a material, L, is proportional to the length: L = L T in which is a constant called the coefficient of linear expansion (whose value depends on the material and on the temperature range of interest). is a measure of the fractional change in length per unit change in temperature. As a general rule, the higher the melting point of the material, the lower the value of .

Volumetric Expansion: solids & liquids • The thermal expansion of a solid is like a three-dimensional enlargement: the previous equation applies to every linear dimension of the object. Hence the volume of the solid will also increase. • For liquids, volume expansion is the only meaningful expansion parameter. Hence we can write the equation for the volumetric expansion of a solid or liquid as: V = V T where V is the original volume, T is the temperature increase, and is the coefficient of volume expansion. Consider a solid block of dimensions a x b x c. The new volume of the block when the temperature is increased T is: V = a (1+ T) x b (1+ T) x c (1+ T) =abc (1 + 3 T + 2 terms + 3 terms) » V 0 (1 + 3 T) 3.

The expansion of water Water has the unusual property that its coefficient of volume expansion becomes zero at 3. 98°C, and is negative between 0°C and 3. 98°C. Ice is also unique in that it is significantly less dense than water – most solids are more dense than their liquid form.

Heat • A hot body when placed in cooler surroundings (e. g. casserole dish taken out of an oven) will undergo a decrease in temperature – rapidly at first and then increasingly slowly – until its temperature equals that of its surroundings. Similarly, a cool body placed in a warmer environment will increase in temperature until its temperature equals that of its surroundings. Q: What is being exchanged between the body and its surroundings that causes this temperature change? A: It is THERMAL or INTERNAL energy collective kinetic and potential energies associated with the random motions of the atoms, molecules, and other microscopic bodies within an object. We call this internal or thermal energy: HEAT Facts about heat: • denoted by the symbol Q and measured in units of Joules (J) • Q is positive when internal energy transferred to a system from its environment • Q is negative when internal energy transferred from a system to its environment

A further definition of heat “Heat is the energy that is transferred between a system and its environment because of a temperature difference that exists between them. ” Work: another form of energy transfer Energy can be transferred between a system and its environment by means of work (symbol W). In this case it requires a force to act upon the system and to displace it (work = force x displacement). Heat capacity (C) is the proportionality constant between the amount of heat either gained or lost by an object, and the temperature change that this produces: Q = C (Tf – Ti) where Ti and Tf are the initial and final temperatures of the object.

Specific heat Two objects made of the same material will have heat capacities proportional to their masses, and so it is convenient to define a “heat capacity per unit mass” or specific heat (c) that refers not to an object but to a unit mass of the material from which it is made. Hence the relationship between heat and temperature change (previous equation) can be written: Q = cm (Tf – Ti) Heats of transformation When a material undergoes a phase change – that is, it changes from a solid to a liquid (or vice-versa), or from a liquid to a gas (or vice-versa) – heat will be either absorbed or released by the material without a change in its temperature: Melting – heat absorbed Vapourisation – heat absorbed Freezing – heat released Condensation – heat released

Heats of transformation The amount of heat per unit mass, m, that must be transferred when a sample completely undergoes a phase change is called the heat of transformation, L: Q=Lm Liquid Gas phase: L is called heat of vapourisation (absorbed) Gas Liquid phase: L is called heat of vapourisation (released) Solid Liquid phase: L is called heat of fusion (absorbed) Liquid Solid phase: L is called heat of fusion (released) Worked example: Q: How much heat is needed to take ice of mass m=0. 72 kg at -10°C to a liquid state at 15°C? A: Need to consider 3 steps: (i)raising the temperature of the ice from -10°C to the melting point at 0°C, (ii)the ice melting at 0°C, and (iii)raising the temperature of the melted ice from 0°C to 15°C.

Worked example contd… Step (i): Q 1 = cice m (Tf – Ti) = (2220 J/kg. K)(0. 72)(0 -)-10) = 15, 984 J Step (ii): Q 2 = LF m = (333000 J/kg)(0. 72 kg) = 239, 800 J Step (iii): Q 3 = cliq m (Tf – Ti) = (4190 J/kg. K)(0. 72)(15 -0) = 45, 252 J Therefore the total heat required is the sum of the heat required for each of the 3 steps: Qtot = Q 1 + Q 2 + Q 3 = 15984 + 239800 + 45252 = 301, 036 J

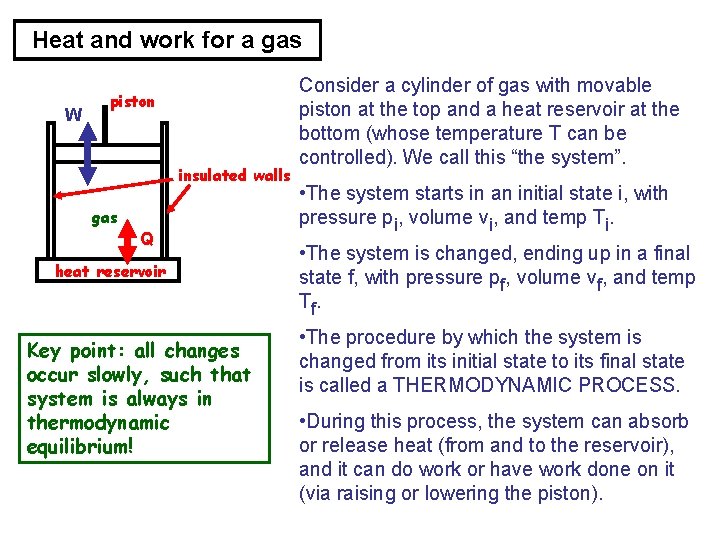
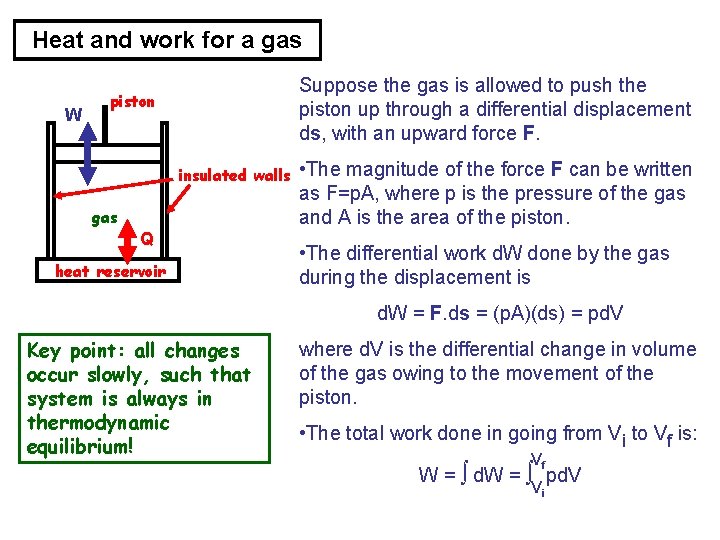
Heat and work for a gas W piston insulated walls gas Q heat reservoir Key point: all changes occur slowly, such that system is always in thermodynamic equilibrium! Consider a cylinder of gas with movable piston at the top and a heat reservoir at the bottom (whose temperature T can be controlled). We call this “the system”. • The system starts in an initial state i, with pressure pi, volume vi, and temp Ti. • The system is changed, ending up in a final state f, with pressure pf, volume vf, and temp Tf. • The procedure by which the system is changed from its initial state to its final state is called a THERMODYNAMIC PROCESS. • During this process, the system can absorb or release heat (from and to the reservoir), and it can do work or have work done on it (via raising or lowering the piston).

Heat and work for a gas W Suppose the gas is allowed to push the piston up through a differential displacement ds, with an upward force F. piston insulated walls gas Q heat reservoir • The magnitude of the force F can be written as F=p. A, where p is the pressure of the gas and A is the area of the piston. • The differential work d. W done by the gas during the displacement is d. W = F. ds = (p. A)(ds) = pd. V Key point: all changes occur slowly, such that system is always in thermodynamic equilibrium! where d. V is the differential change in volume of the gas owing to the movement of the piston. • The total work done in going from Vi to Vf is: Vf W = ∫ d. W = ∫ pd. V Vi

(courtesy of Halliday, Resnick, Walker, 4 th Edition) There are many ways to take the gas from state i to state f, and this is best shown in a p-V diagram: (a) Simple drop in pressure with increase in volume: W = area under (green) curve, which is positive gas did positive work. (b) Two steps, one at constant p and one at constant V: Only the first (ia) involves work, which is positive, and would require heating the gas (from Ti to Ta, so it expands), while maintaining a constant pressure on the piston. Step af requires keeping the gas at a constant volume (by keeping the piston fixed), and reducing the pressure by reducing the temperature (from Ta to Tf). Heat is lost from the gas. (c) Two steps of (b) are carried out in reverse order: W is smaller, as is the net heat absorbed. (d) W can be as small (icdf) or as large (ighf) as you want depending on path.

(e) Negative work is done by the system through some external force compressing it. (f) A thermodynamic cycle where the system goes from initial state i to final state f and then back to i again. The net work done by the system is the sum of the positive work done during the expansion and the negative work done during the compression. Wnet > 0. (courtesy of Halliday, Resnick, Walker, 4 th Edition)

The First Law of Thermodynamics • We have just seen that the various paths taken on the p-V diagram in going from an initial state i to final state f, can involve both changes in Q (heat) and W (work done by the system). • Experimentally we find that the quantity Q-W is the same for all processes • In other words, Q-W depends only on the initial and final states and not on the path taken between! • The quantity Q-W must therefore represent some intrinsic property of the system: We call this the Internal Energy (Eint) of the system Eint = Eint, f – Eint, I Eint = Q-W 1 st Law of Thermodynamics Note: W = the work done by the system (not on the system)

Special cases of the 1 st Law Process Restriction Consequence Adiabatic Q=0 Eint = -W Constant volume W=0 Eint = Q Closed cycle Eint = 0 Q=W Free expansion Q=W=0 Eint = 0

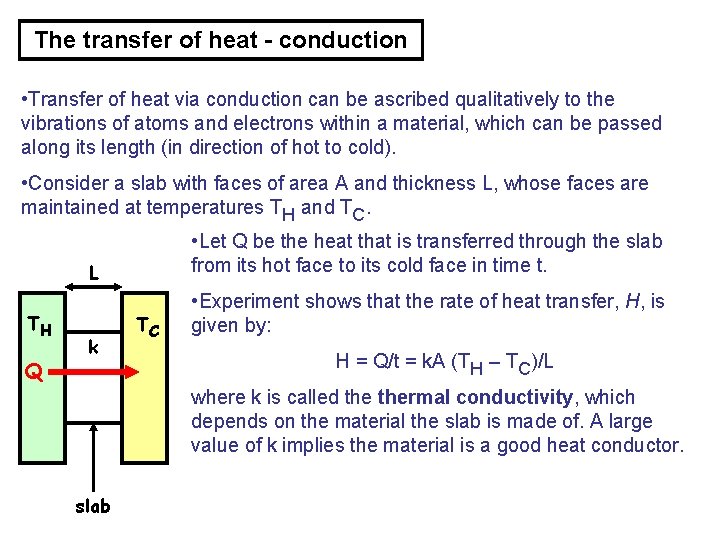
The transfer of heat - conduction • Transfer of heat via conduction can be ascribed qualitatively to the vibrations of atoms and electrons within a material, which can be passed along its length (in direction of hot to cold). • Consider a slab with faces of area A and thickness L, whose faces are maintained at temperatures TH and TC. • Let Q be the heat that is transferred through the slab from its hot face to its cold face in time t. L TH Q k TC • Experiment shows that the rate of heat transfer, H, is given by: H = Q/t = k. A (TH – TC)/L where k is called thermal conductivity, which depends on the material the slab is made of. A large value of k implies the material is a good heat conductor. slab

Thermal resistance to conductance (R-value) • The opposite to good conduction is good insulation and we can think of this in terms of thermal resistance R. The R-value of a slab of thickness L is defined as: R = L/k • Thus the lower thermal conductivity of the material (i. e. the lower the value of k), the higher its R-value is. • Substituting the above definition of R into the equation for H gives: H = A (TH – TC) / R Some k and R-values for various materials: Material k (W/m. K) R-value Copper 401 0. 00036 Lead 35 0. 0041 Silver 428 0. 00034 Aluminium 235 0. 00061 Air 0. 026 5. 5 Poly-foam 0. 024 5. 9 Fiberglass 0. 048 3. 0 Window glass 1. 0 0. 14

Conduction through a composite slab TH Q L 2 L 1 k 2 k 1 TX TC Consider a composite slab, consisting of two materials having different thickness, L 1 and L 2, and different thermal conductivities, k 1 and k 2. The outer surfaces of the slab are in contact with a heat reservoir of temperature TH (left end) and TC (right end). Each face of the slab has area A. Temperature at the boundary of two materials is TX. Assumption: heat transfer through the slab is a steady -state process – temperatures throughout the slab and the rate of heat transfer do not change with time. In the steady-state, the rates of heat transfer through the two materials are the same, hence: H = Q/t = k 2 A(TH – TX)/L 2 = k 1 A(TX-TC)/L 1 Solving for TX then gives: TX = (k 1 L 2 TC+k 2 L 1 TH)/(k 1 L 2+k 2 L 1) and substituting back in to previous equation: H = A(TH – TC)/ [(L 1/k 1) + L 2/k 2)]

Conduction through a multi-composite slab The previous equation for the rate of heat transfer through a composite slab of two materials: H = A(TH – TC)/ [(L 1/k 1) + L 2/k 2)] can be generalised for any number of materials to: H = A(TH – TC)/ (L/k) = A(TH – TC)/ R

Kinetic Theory of Gases – Heat at the Microscopic Level • Up until now we have been concerned only with the macroscopic behaviour of bodies when talking about their thermal properties and the transfer of heat between them. Moreover, the main physical quantities we have been using in this context – pressure, volume, temperature, work, internal energy – have all been understood and applied in a macroscopic sense. • The kinetic theory of gases attempts to understand these quantities in a microscopic way: for example, Q. why does gas exert a pressure? A. because of the constant collisions the atoms/molecules of the gas are having with the wall of the container. Also these same motions give the gas temperature and internal energy. Ideal Gases • A problem in attempting to describe the microscopic behaviour of gases via general laws is that they are all slightly different in their behaviour. However, it has been found by experimentation that as you go to lower and lower gas densities, all gases tend towards having the same behaviour. An ideal gas is one that exhibits this behaviour in the low-density limit.

Ideal Gases So what is this behaviour? ? An ideal gas exhibits the following relation between pressure, p, volume, V, and temperature, T: p. V = n. RT (Ideal Gas Law) where n is the number of moles of gas present (1 mole = Avagadro’s Number of molecules = 6. 02 x 1023), and R is the gas constant (=8. 31 J/mol. K). Note: T must be expressed in degrees Kelvin!! Work done by an Ideal Gas at Constant Temperature Suppose that a sample of n moles of an ideal gas confined to a cylinder with a piston at one end, is allowed to expand from an initial volume Vi to a final volume Vf. The temperature, T, is held constant throughout the process an isothermal expansion. The work W done by the gas is: Vf W = ∫ pd. V Vi And we can subsitute in for p from the Ideal Gas Law: W = ∫ f(n. RT/V)d. V

Work done by an Ideal Gas at Constant Temperature Vf W = ∫V (n. RT/V)d. V i and since T is constant: Vf W = n. RT ∫V d. V/V i W = n. RT ln (Vf/Vi) Worked example: A cylinder contains 12 litres of oxygen at 293 K and 15 atm. The temperature is raised to 308 K and the volume reduced to 8. 5 litres. What is the final pressure of the gas (assuming it is ideal)? The ideal gas law can be written as (pi. Vi/Ti) = (pf. Vf/Tf) Rearranging and plugging in data: pf=[(15)(308)(12)]/[(293)(8. 5)] = 22 atm

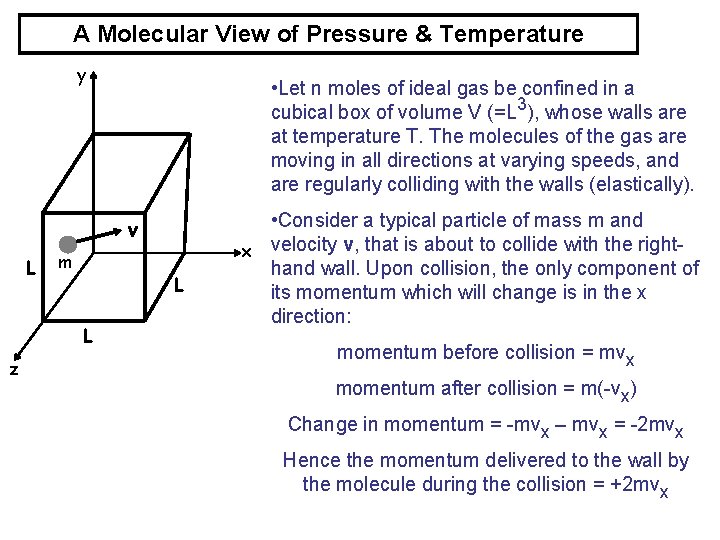
A Molecular View of Pressure & Temperature y • Let n moles of ideal gas be confined in a cubical box of volume V (=L 3), whose walls are at temperature T. The molecules of the gas are moving in all directions at varying speeds, and are regularly colliding with the walls (elastically). v L m L L z • Consider a typical particle of mass m and x velocity v, that is about to collide with the righthand wall. Upon collision, the only component of its momentum which will change is in the x direction: momentum before collision = mvx momentum after collision = m(-vx) Change in momentum = -mvx – mvx = -2 mvx Hence the momentum delivered to the wall by the molecule during the collision = +2 mvx

A Molecular View of Pressure & Temperature y • The molecule will hit the wall repeatedly, and we can calculate how often it will do this: • Time taken to travel from right-hand wall to lefthand wall and back again = 2 x (L/vx) v L m L L z x • Thus the rate at which momentum is delivered to the right-hand wall is given by: p/ t = 2 mvx/2 L/vx = mv 2 x/L • From Newton’s 2 nd law, the rate at which momentum is delivered to the wall equals the force, F, exerted on the wall by the molecule. • We need to add up the contributions from all molecules to get the total force on the wall, and divide it by the area of the wall to get the pressure, p: p=F/L 2 = [mvx 12/L+mvx 22/L+…. +mvx. N 2/L]/L 2 = (m/L 3)(vx 12+vx 22+…+vx. N 2) (N = number of molecules in box)

A Molecular View of Pressure & Temperature y • Since N = n. NA and <vx 2> = (vxn 2)/N, we can write the previous equation as: p =(m/L 3)N<vx 2> =(nm. NA/L 3)<vx 2> v L m L L z • But m. NA is the molar mass M of the gas (that is, the mass of 1 mole of the gas), and L 3 is the x volume of the box, so p = n. M<vx 2>/V • For any molecule v 2 = vx 2 + vy 2 + vz 2, and because they are all moving in random directions, the average values of the squares of their velocity components are equal so that vx 2 = ⅓ v 2 and so the previous equation can be written as: p = n. M<v 2>/3 V

A Molecular View of Pressure & Temperature y • Now the square root of <v 2> is called the root mean square speed, and is symbolised by vrms. So we can express the pressure in terms of this quantity: p = n. Mvrms 2/3 V v L m L L z x or p. V = ⅓ n. Mvrms 2 • Finally, if we take the ideal gas law: p. V = n. RT and combine it with the previous expression, we get: vrms = 3 RT/M Values of vrms (in km/s) for various molecules at room temperature (300 K): H 2=1920, He=1370, water vapour = 645, N 2=517, O 2=483, CO 2=412, S 02=342

Translational Kinetic Energy • Consider the single gas molecule (of mass m) moving inside the box as per the previous section. Its translational kinetic energy at any instant is ½mv 2. Its average kinetic energy over time is: <K> = <½mv 2> = ½m<v 2> = ½mvrms 2 Note the assumption that is made here: the average speed of the molecule is the same as the average speed of all the molecules at any given time. • Now we have shown that vrms = 3 RT/M, so we can write <K> as: <K> = ½m (3 RT/M) But M/m is the molar mass divided by the mass of the molecule, which is simply Avagadro’s Number, NA, so: <K>=(3 RT)/2 NA or <K> = (3/2)k. T where k = Boltzmann’s constant = R/NA (= 1. 38 x 10 -23 J/K)

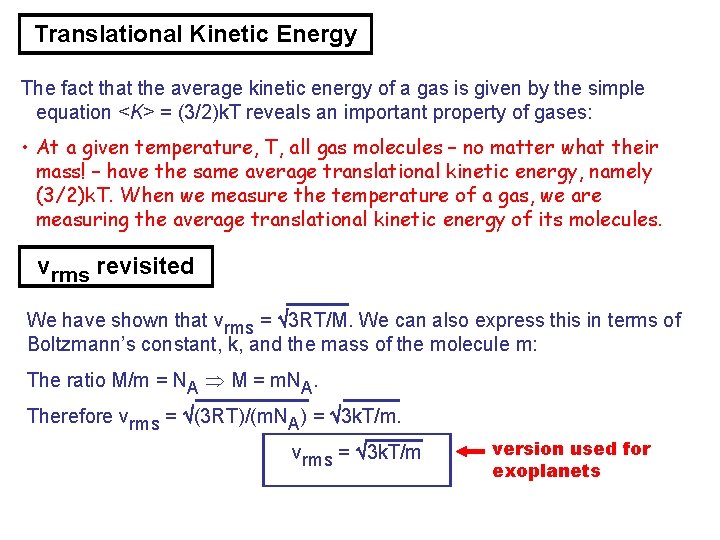
Translational Kinetic Energy The fact that the average kinetic energy of a gas is given by the simple equation <K> = (3/2)k. T reveals an important property of gases: • At a given temperature, T, all gas molecules – no matter what their mass! – have the same average translational kinetic energy, namely (3/2)k. T. When we measure the temperature of a gas, we are measuring the average translational kinetic energy of its molecules. vrms revisited We have shown that vrms = 3 RT/M. We can also express this in terms of Boltzmann’s constant, k, and the mass of the molecule m: The ratio M/m = NA M = m. NA. Therefore vrms = (3 RT)/(m. NA) = 3 k. T/m. vrms = 3 k. T/m version used for exoplanets

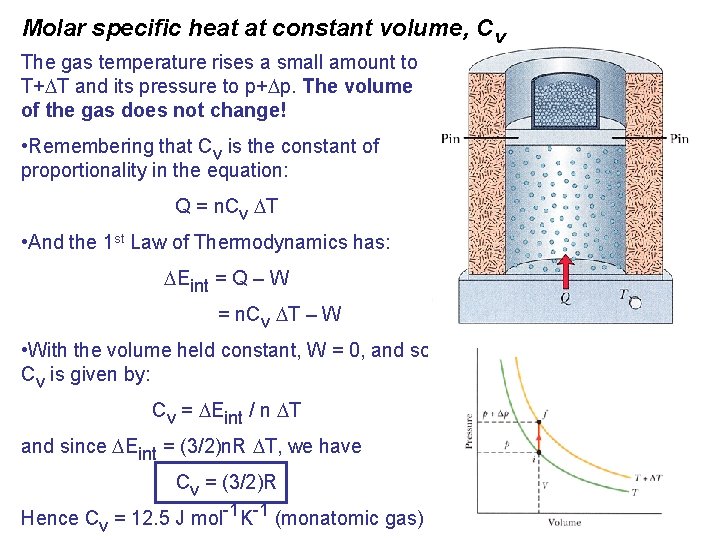
Heat Capacities of an Ideal Gas We now take a microscopic approach to understanding the heat capacity of an ideal gas – that is, the proportionality relationship between heat (or internal energy) and temperature change, per unit mass of gas. • Our previous derivation of mean kinetic energy, <K>, leads naturally into defining what the internal energy, Eint, for an ideal gas is: it is the sum of the translational kinetic energies of its molecules. Hence a sample of n moles of such as gas contains n. NA molecules, so Eint is simply: Eint = (n. NA) <K> = (n. NA)(3/2)(k. T) And since NAk = R, the gas constant, then: Eint = (3/2)n. RT (monatomic ideal gas). Molar specific heat at constant volume, Cv Consider the cylinder and piston arrangement again, enclosed in which is n moles of an ideal gas at pressure p and temperature T. The volume of the cylinder is V. Suppose the gas is taken from this initial state to a final state by adding a small amount of heat Q to the gas by slowly increasing the temperature of the reservoir.

Molar specific heat at constant volume, Cv The gas temperature rises a small amount to T+ T and its pressure to p+ p. The volume of the gas does not change! • Remembering that Cv is the constant of proportionality in the equation: Q = n. Cv T • And the 1 st Law of Thermodynamics has: Eint = Q – W = n. Cv T – W • With the volume held constant, W = 0, and so Cv is given by: Cv = Eint / n T and since Eint = (3/2)n. R T, we have Cv = (3/2)R Hence Cv = 12. 5 J mol-1 K-1 (monatomic gas)

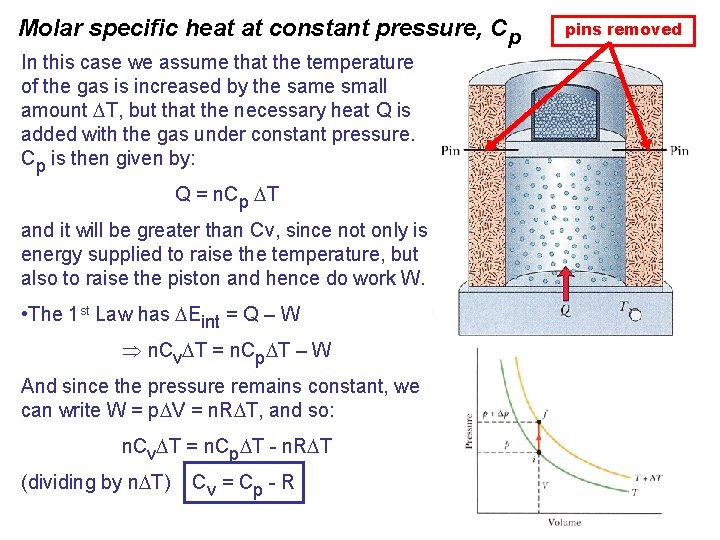
Molar specific heat at constant pressure, Cp In this case we assume that the temperature of the gas is increased by the same small amount T, but that the necessary heat Q is added with the gas under constant pressure. Cp is then given by: Q = n. Cp T and it will be greater than Cv, since not only is energy supplied to raise the temperature, but also to raise the piston and hence do work W. • The 1 st Law has Eint = Q – W n. Cv T = n. Cp T – W And since the pressure remains constant, we can write W = p V = n. R T, and so: n. Cv T = n. Cp T - n. R T (dividing by n T) Cv = C p - R pins removed

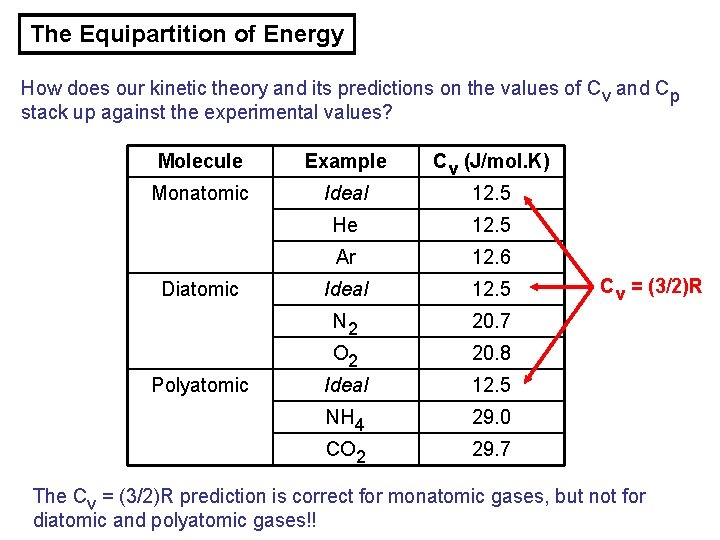
The Equipartition of Energy How does our kinetic theory and its predictions on the values of Cv and Cp stack up against the experimental values? Molecule Example Cv (J/mol. K) Monatomic Ideal 12. 5 He 12. 5 Ar 12. 6 Ideal 12. 5 N 2 20. 7 O 2 20. 8 Ideal 12. 5 NH 4 29. 0 CO 2 29. 7 Diatomic Polyatomic Cv = (3/2)R The Cv = (3/2)R prediction is correct for monatomic gases, but not for diatomic and polyatomic gases!!

The Equipartition of Energy The Cv = (3/2)R prediction is correct for monatomic gases, but not for diatomic and polyatomic gases!! – WHY IS THIS SO? ? Monatomic molecules, which are point like, can only possess one type of energy and that is translational kinetic energy. Diatomic and polyatomic molecules can possess other forms of energy by rotating and vibrating! Maxwell’s theorem on the equipartition of energy: “Every kind of molecule has a certain number f of degrees of freedom which are independent ways in which it can store energy. Each such degree of freedom has associated with it, on average, an energy of ½k. T per molecule. ” For translational motion, there are 3 degrees of freedom, corresponding to the x, y, z directions. For rotational motion, a monatomic molecule has 0 degrees of freedom, a diatomic molecule has 2 degrees of freedom (along the 2 axes that are perpindicular to the axis that joins the two atoms).

The Equipartition of Energy A molecule with more than two atoms has 6 degrees of freedom: 3 translational and 3 rotational. How does this carry over into the derivation of specific heat: Instead of Eint = (3/2)n. RT Eint = (f/2)n. RT where f = number of degrees of feedom. This then gives: Cv = (f/2)R = 4. 16 f J/mol. K Molecule Example f(trans) f(rot) f(total) Cv (pred) Cv (obs) Monatomic He 3 0 3 (3/2)R=12. 5 Diatomic O 2 3 2 5 (5/2)R =20. 8 Polyatomic CH 4 3 3 6 3 R= 25. 0 29. 4 X

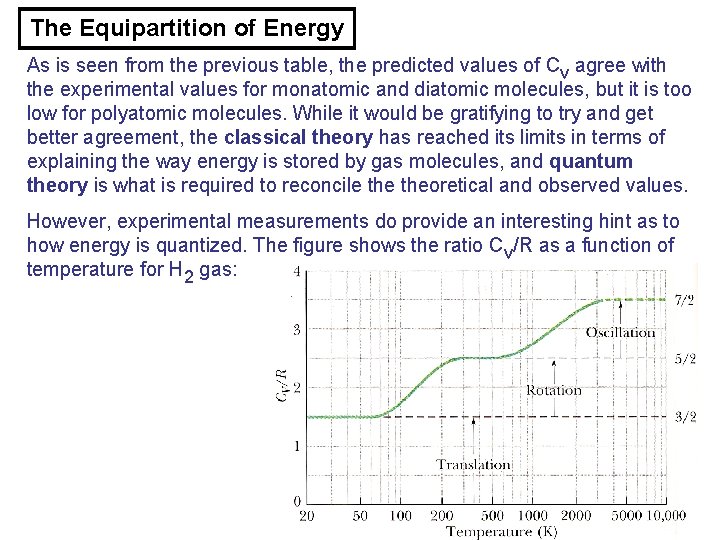
The Equipartition of Energy As is seen from the previous table, the predicted values of Cv agree with the experimental values for monatomic and diatomic molecules, but it is too low for polyatomic molecules. While it would be gratifying to try and get better agreement, the classical theory has reached its limits in terms of explaining the way energy is stored by gas molecules, and quantum theory is what is required to reconcile theoretical and observed values. However, experimental measurements do provide an interesting hint as to how energy is quantized. The figure shows the ratio Cv/R as a function of temperature for H 2 gas:

The Equipartition of Energy • Below 80 K, Cv/R = 1. 5 gas behaves as though it is monatomic (even though H 2 is diatomic). Only translational modes of motion are excited. • At T=100 -200 K, Cv/R = 2. 5 and clearly rotational modes become excited. • At above T~3000 K, Cv/R=3. 5 and vibrational modes become excited; however, H 2 molecule dissociates at about T=3200 K.

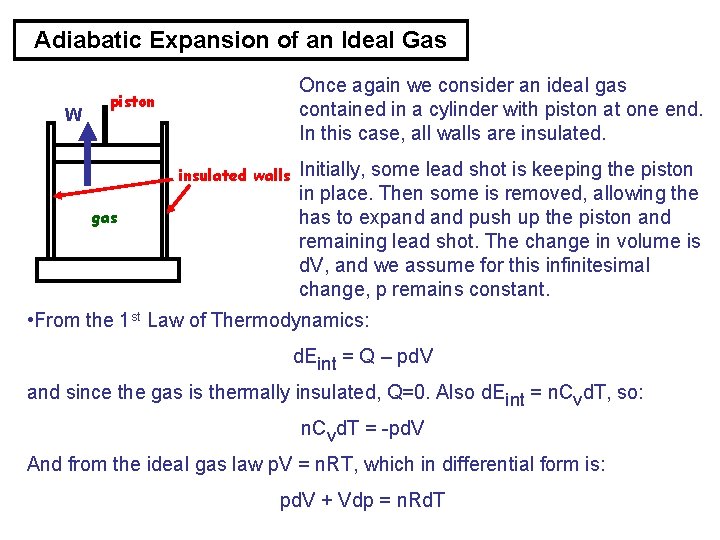
Adiabatic Expansion of an Ideal Gas W Once again we consider an ideal gas contained in a cylinder with piston at one end. In this case, all walls are insulated. piston insulated walls gas Initially, some lead shot is keeping the piston in place. Then some is removed, allowing the has to expand push up the piston and remaining lead shot. The change in volume is d. V, and we assume for this infinitesimal change, p remains constant. • From the 1 st Law of Thermodynamics: d. Eint = Q – pd. V and since the gas is thermally insulated, Q=0. Also d. Eint = n. Cvd. T, so: n. Cvd. T = -pd. V And from the ideal gas law p. V = n. RT, which in differential form is: pd. V + Vdp = n. Rd. T

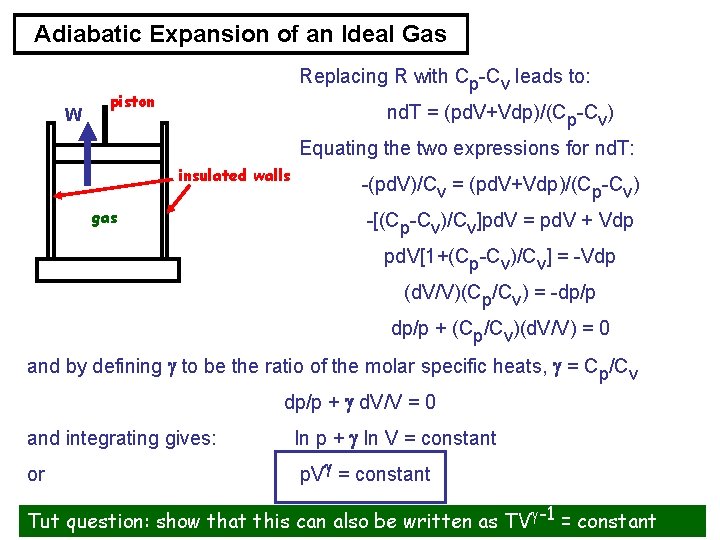
Adiabatic Expansion of an Ideal Gas W Replacing R with Cp-Cv leads to: piston nd. T = (pd. V+Vdp)/(Cp-Cv) Equating the two expressions for nd. T: insulated walls gas -(pd. V)/Cv = (pd. V+Vdp)/(Cp-Cv) -[(Cp-Cv)/Cv]pd. V = pd. V + Vdp pd. V[1+(Cp-Cv)/Cv] = -Vdp (d. V/V)(Cp/Cv) = -dp/p + (Cp/Cv)(d. V/V) = 0 and by defining to be the ratio of the molar specific heats, = Cp/Cv dp/p + d. V/V = 0 and integrating gives: ln p + ln V = constant or p. V = constant Tut question: show that this can also be written as TV -1 = constant