Thermal Physics 3 Modular Kinetic Theory Elliott Modular

Thermal Physics (3) Modular Kinetic Theory Elliott

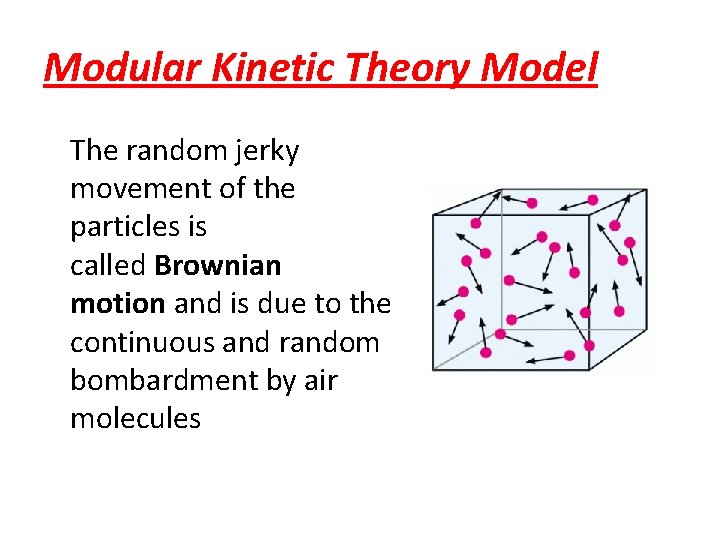
Modular Kinetic Theory Model The random jerky movement of the particles is called Brownian motion and is due to the continuous and random bombardment by air molecules

Pressure Exerted by an Ideal Gas • Pressure is exerted by the impact of molecules on the sides of a container. .

Gas pressure equations based on the following assumptions: • The gas consists of a large number of identical molecules • All collisions between molecules and the walls of the container are perfectly elastic. • Intermolecular forces are negligible, as is gravity. • Molecules move in straight lines and at constant speed between collisions. • Collision times are negligible compared with time between collisions. • Volume of the gas molecules is negligible compared to that of the gas. • Newton’s laws of motion are applicable

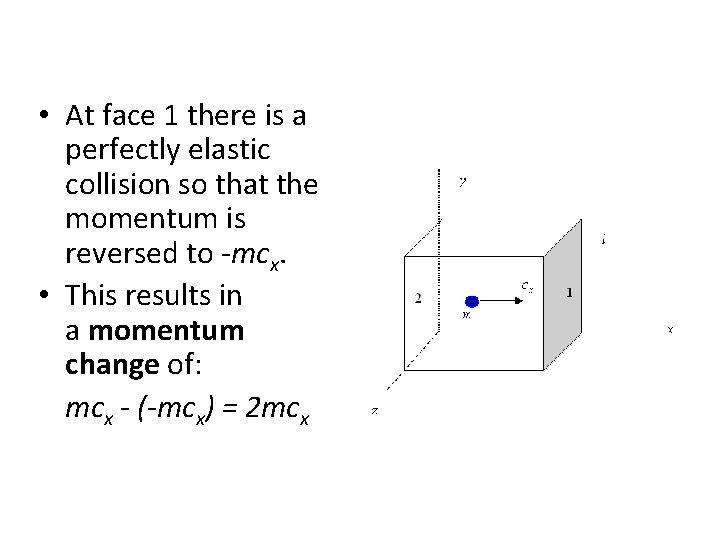
Stage 1 Momentum Change • Consider a large box, side l, full of molecules: • Now consider one molecule of mass m moving towards face 1 and the xcomponent of its velocity is cx. • -> its momentum in the x direction is mcx

• At face 1 there is a perfectly elastic collision so that the momentum is reversed to -mcx. • This results in a momentum change of: mcx - (-mcx) = 2 mcx

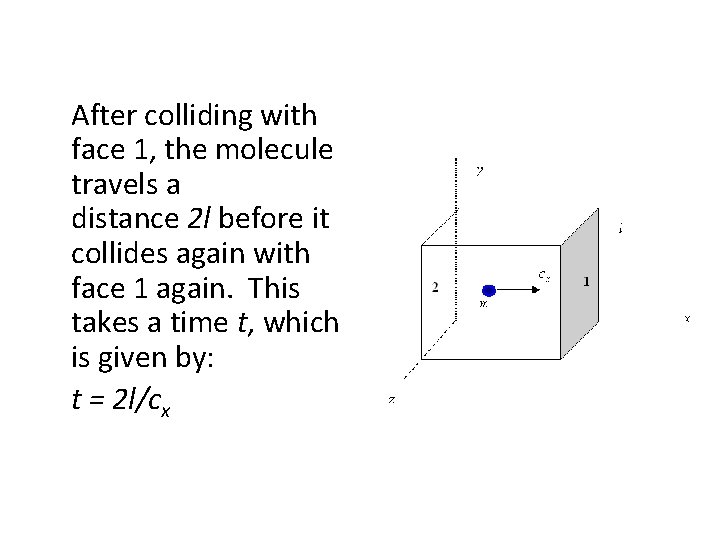
After colliding with face 1, the molecule travels a distance 2 l before it collides again with face 1 again. This takes a time t, which is given by: t = 2 l/cx

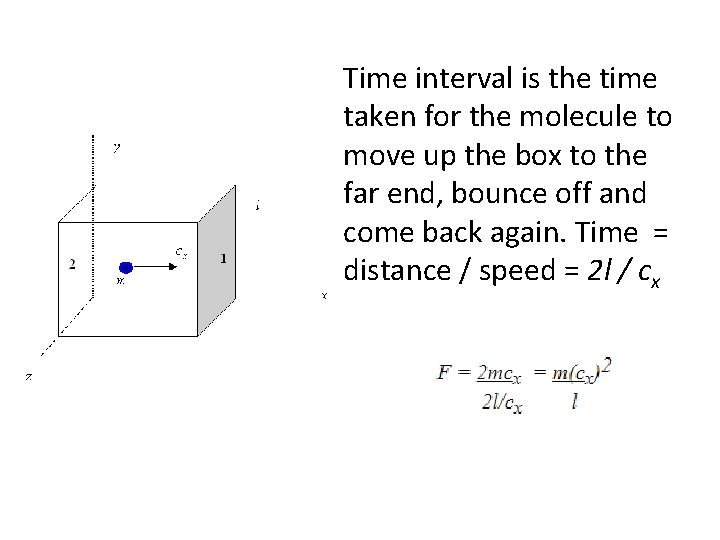
Stage 2 - Impulse So that we can get the pressure, we need to know the force. This can be worked out by Newton II, considering the impulse, which is the change of momentum.

Time interval is the time taken for the molecule to move up the box to the far end, bounce off and come back again. Time = distance / speed = 2 l / cx

Stage 3 - Pressure • Since pressure = force/area, we can work out the pressure on face 1. • The area of face 1 = l 2.

Adjust for Moles Suppose we have N molecules of gas. The pressure will be: