Theory of Information Lecture 3 Strings and Things

Theory of Information Lecture 3 Strings and Things (Section 1. 1) 1

Congruency Modulo n Remember that Zn={0, 1, …, n-1} If and are integers, the following three conditions are equivalent: 1. and have the same remainder when divided by n 2. - is divisible by n 3. there is an integer k for which = +kn When any (and hence all) of these conditions hold, we say that and are congruent modulo n, and write (mod n) 2

Examples of Congruency 5 3(mod 2)? 14 143(mod 2)? 144 10(mod 5)? 1934 124(mod 10)? -5 15(mod 5)? -7 8(mod 2)? -5 -2 1 4 7 10 13 16(mod 3)? 3

Residue Given an integer , there is exactly one element in Zn congruent to (modulo n). Such an integer is called the residue of modulo n. The residue of 25 modulo 7 is The residue of 32 modulo 7 is The residue of 9925 modulo 2 is The residue of 8764 modulo 2 is Give me a number whose residue modulo 7 is 7 4

Modular Arithmetic Let a, b Zn. It, together with the following operations, is called integers modulo n: a+nb= the residue of a+b modulo n a nb= the residue of a b modulo n Z 5={0, 1, 2, 3, 4}. Let us just write + and instead of +5 and 5. 1+3= 1+4= 2+3= 4+4= 2 3= 4 4= 0 4= 1 4= 0+3= 5

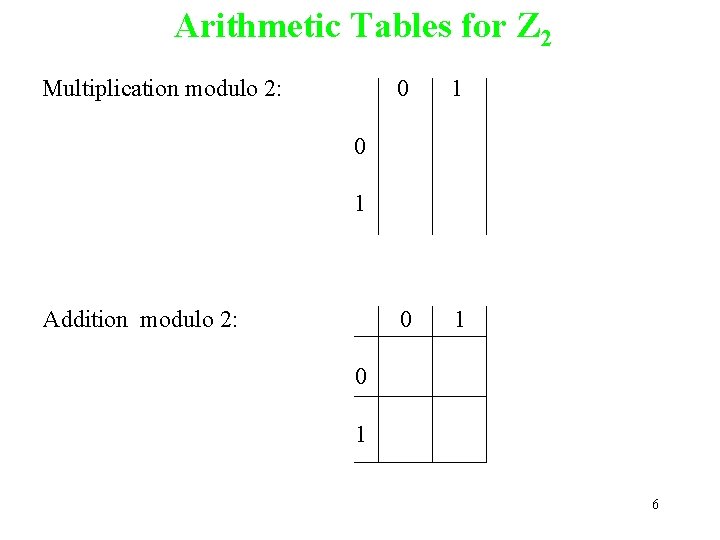
Arithmetic Tables for Z 2 Multiplication modulo 2: 0 1 0 1 Addition modulo 2: 0 1 6

Fields DEFINITION A field is a nonempty set F, together with two binary operations on F, called addition (+) and multiplication ( , often omitted), satisfying the following properties: 1. Associativity: +( + )=( + )+ ; ( )=( ). 2. Commutativity: + = + ; = . 3. Distributivity: ( + )= + . 4. Properties of 0 and 1: There are two distinct ( ) elements: 0 (zero) and 1 (one) such that, for all F, we have 0+ = and 1 =. 5. Inverse properties: a) For every F, there is another element of F denoted by - and called the negative of , such that +(- )=0; b) For every nonzero F, there is another element of F denoted by -1 and called the inverse of , such that ( -1)=1. With ordinary addition and multiplication, are the following sets fields? {0, 1, …} {…-2, -1, 0, 1, 2, …} The set of rational numbers 7

Integers Modulo 2 Is a Field For Z 2={0, 1} (as well as all other Zn), associativity, commutativity and distributivity hold because they hold for the ordinary + and . What is the negative of: 0? 1? What is the inverse of: 1? Subtraction - means +(- ). In our case, 0 -0= 0 -1= 1 -0= 1 -1= 8

Integers Modulo 3 Is a Field What is the negative of: 0? 1? 2? What is the inverse of: 1? 2? 9

Integers Modulo 4 Is not a Field Z 2={0, 1, 2, 3} What would be the inverse of 2? 2 0= 2 1= 2 2= 2 3= 10

When is Zn a field? An integer n is said to be prime iff n has no divisors other than 1 and n. Prime numbers: 2, 3, 7, 11, 13, 17, 19, 23, 29, 31, 41, … THEOREM 1. 1. 2 The set Zn of integers modulo n is a field if and only if n is a prime number. 11

Strings An alphabet is a finite, nonempty set S={s 1, …, sn} of symbols. A string, or word over S is a finite sequence of elements of S. E. g. , when S={a, b, …, z}, then school, bbb, a, xyz are strings/words over S. So is the empty string (theta). Stings over the alphabet {0, 1} are called binary strings, and the symbols 0 and 1 are called bits. The complement of a binary string x is the result of replacing in x every 0 by 1 and every 1 by 0. Denoted by xc. Strings over {0, 1, 2} are called ternary strings. 12

Strings The juxtaposition (concatenation) of strings x and y is xy. len(x) denotes the length of string x. len(0010)=4, len(0)=1, len( )=0. When S is an alphabet: S* stands for the set of all strings over S Sn stands for the set of all strings over S whose length is n THEOREM 1. 1. 3 Let S be an alphabet of size k. 1. |Sn|=kn 2. |Sn|= 1+k+k 2+…+kn 13

Strings THEOREM 1. 1. 4 n n 1. In (Z 2) , the number of strings with exactly k 0 s is (k ) n 2. In (Zr)n, the number of strings with exactly k 0 s is (k )(r-1)n-k Proof. Part 1: There is one string with exactly k 0 s for every way of choosing k of the n positions in which to place 0 s. Part 2: For each choice of where to place 0 s, there are (r-1)n-k ways to arrange the remaining (r-1) symbols in the remaining (n-k) positions. 14

Homework Example 1. 1. 4 of the textbook. Exercises 1, 3, 4, 5, 7, 8 of Section 1. 1 of the textbook. 15