Theory of Information Lecture 14 Decision Rules Nearest

Theory of Information Lecture 14 Decision Rules, Nearest Neighbor Decoding (Section 4. 2, 4. 3) 1

What Is a Decision Rule? Communications channel model encoded received message …x… message … … noise decoded message decision rule An (n, M)-code means a block code of length n and size M (i. e. every codeword has length n, and there are M codewords altogether) Definition Let C be an (n, M)-code over a code alphabet A, and assume C does not contain the symbol ? . A decision rule for C is a function f: An C {? }. Intuition: f(x)=c means assuming that the received word x was meant to be c, i. e. that c was sent. In other words, decoding, or interpreting x as c. If we cannot identify such a codeword, i. e. c C, the symbol ? is used to declare a decoding error, 2 so in this case always c=? .

Two Sorts of Decision Rules Goal: maximize the probability of correct decoding Code alphabet: {0, 1} Code: {0000, 1111} 0 90% 0 10% Channel: 11% 1 89% 1 If 0111 is received, how would you interpret it? If 0011 is received, how would you interpret it? But if you knew that 1111 is sent 99% of the time, how would you interpret 0011? 3

Which Rule Is Better? Ideal observer decision rule Maximum likelihood decision rule Advantages: 4

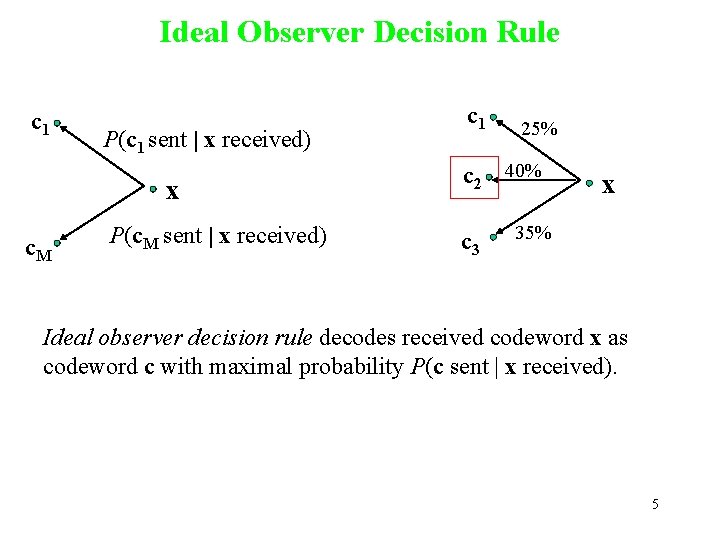
Ideal Observer Decision Rule c 1 P(c 1 sent | x received) x c. M P(c. M sent | x received) c 1 25% c 2 40% c 3 x 35% Ideal observer decision rule decodes received codeword x as codeword c with maximal probability P(c sent | x received). 5

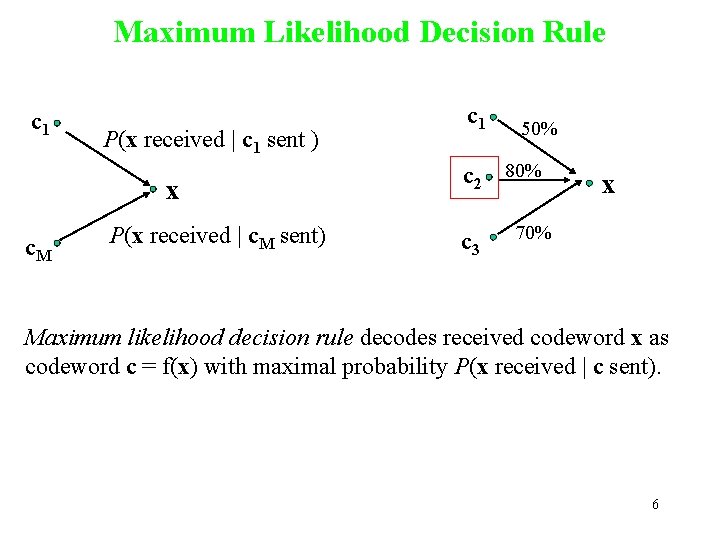
Maximum Likelihood Decision Rule c 1 P(x received | c 1 sent ) x c. M P(x received | c. M sent) c 1 50% c 2 80% c 3 x 70% Maximum likelihood decision rule decodes received codeword x as codeword c = f(x) with maximal probability P(x received | c sent). 6

One Rule as a Special Case of the Other c 1 Assume all codewords are equally likely to be sent. What would be the backward probabilities then? 50% c 2 80% c 3 x 70% c 1 c 2 x c 3 Theorem 4. 2. 2: For the uniform input distribution, ideal observer decoding coincides with maximum likelihood decoding. 7

Example 4. 2. 1 Suppose codewords of C = {000, 111} are sent over a binary symmetric channel with crossover prob. p = 0. 01. If string 100 is received, how should it be decoded by the m a x i m u m l i k e l i h o o d d e c i s i o n r u l e ? P(100 received | 000 sent)= P(100 received | 111 sent)= Would the same necessarily be the case under ideal observer decoding? 8

Sometimes the Two Rules Yield Different Results 95% 0 0 5% 6% 1 94% 1 Assume: C={00, 11}; 11 is sent 70% of the time; 01 is received. How would 01 be decoded by the maximum likelihood rule? As How would 01 be decoded by the ideal observer rule? As 9

Handling Ties In the case of ties, it is reasonable for a given decision rule to declare an error. Suppose codewords of C = {0000, 1111} are sent over a binary symmetric channel with crossover prob. p = ¼. How should the following strings be decoded by the m a x i m u m l i k e l i h o o d d e c i s i o n r u l e ? 0 0 1 0 1 1 0 0 1 1 P(0011 received | 0000 sent)= P(0011 received | 1111 sent)= 10

Hamming Distance and Nearest Neighbor Decoding Definition Let x and y be two strings of the same length over the same alphabet. The Hamming distance between x and y, denoted d(x, y), is defined to be the number of places in which x and y differ. E. g. : d(000, 100) = 1, d(111, 100) = 2. The decision rule assigning a received word the closest codeword (in Hamming distance) is called the nearest neighbor decision rule. Theorem 4. 3. 2 For BSC, the maximum likelihood decision rule is equivalent to the nearest neighbor decision rule. 11

Exercise 7 of Section 4. 3 Construct a binary channel for which maximum likelihood decoding is not the same as nearest neighbor decoding. 0 10% 0 Let C= {001, 011} Assume 000 is received. 90% 50% 1 P(000 received | 001 sent) = P(000 received | 011 sent) = 12

Homework Exercises 2, 3, 4, 5 of Section 4. 2. Exercises 1, 2, 3 of Section 4. 3. 13