Theory of Computation Turing Machine TM Lecture 13

Theory of Computation Turing Machine TM Lecture #13

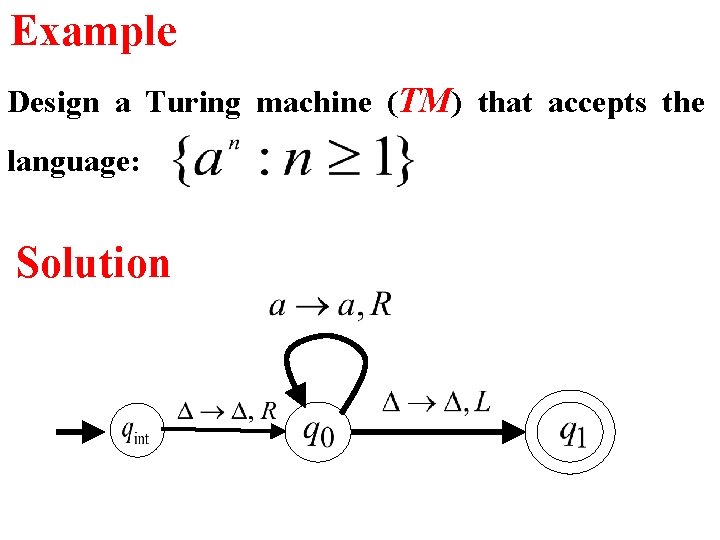
Example Design a Turing machine (TM) that accepts the language: Solution

Computing Functions with Turing Machines

A function Domain Result Region has:

Integer Domain: Unary: 11111 Binary: 101 Decimal: 5 Prefer Unary representation: Easier to manipulate

A function may have many parameters: Example: Addition function are integers

Definition: A function is computable if there is a Turing Machine such that: final state Initial Configuration Final configuration Domain

In other words: A function is computable if there is a Turing Machine such that: Initial Configuration Final Configuration Domain

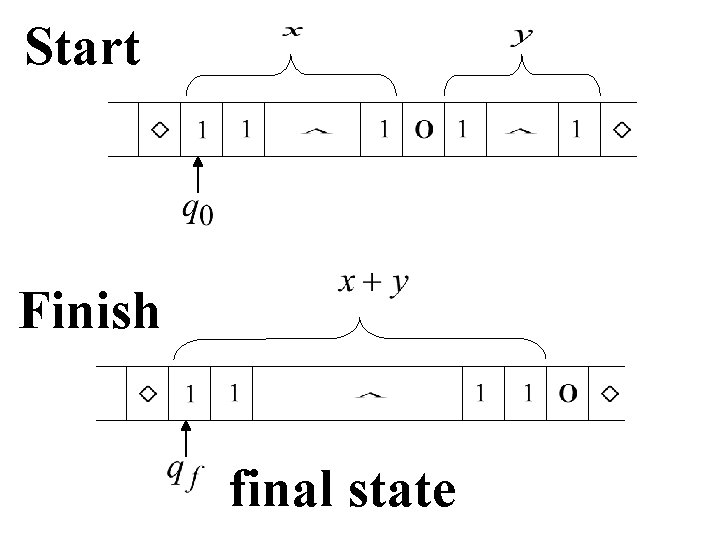
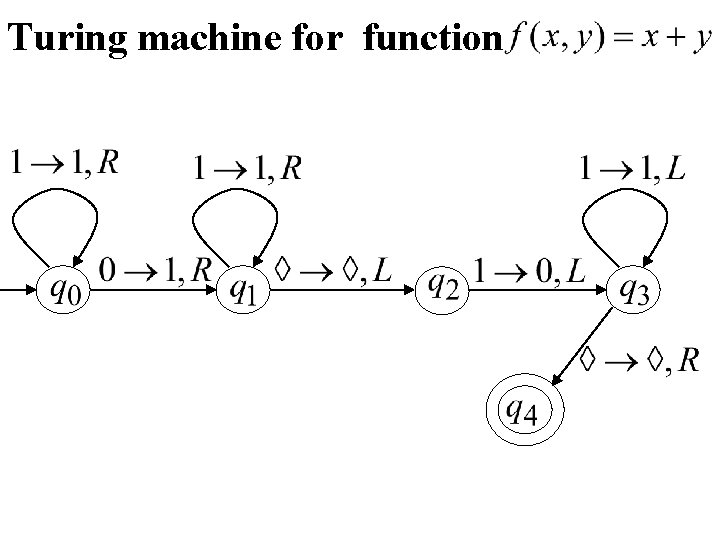
Example The function is computable are integers Turing Machine: Input string: unary Output string: unary

Start Finish final state

Turing machine for function

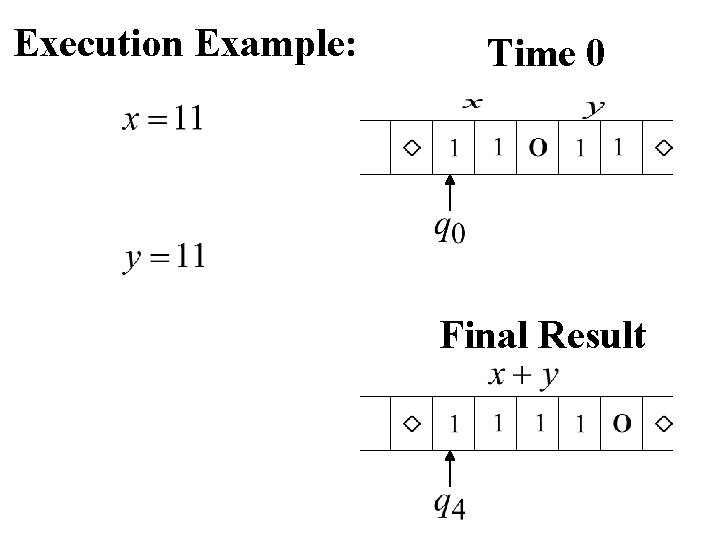
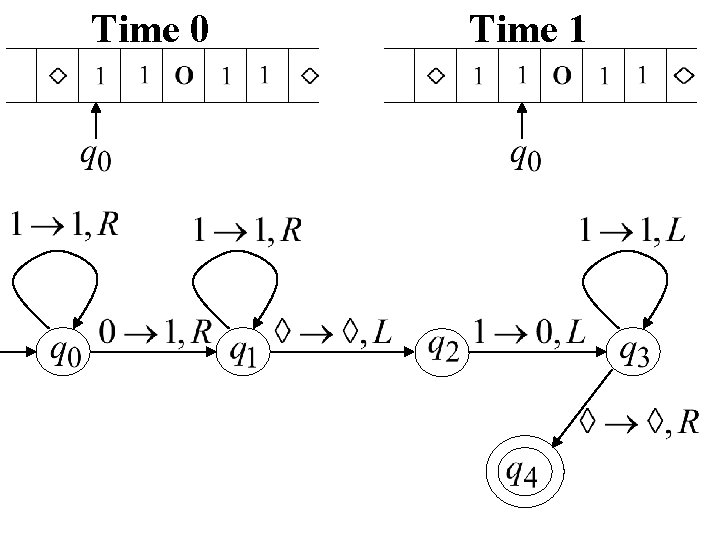
Execution Example: Time 0 Final Result

Time 0 Time 1

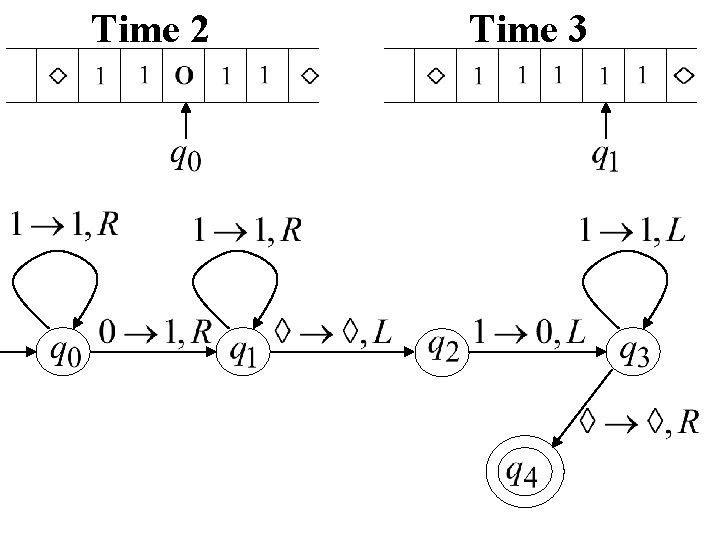
Time 2 Time 3

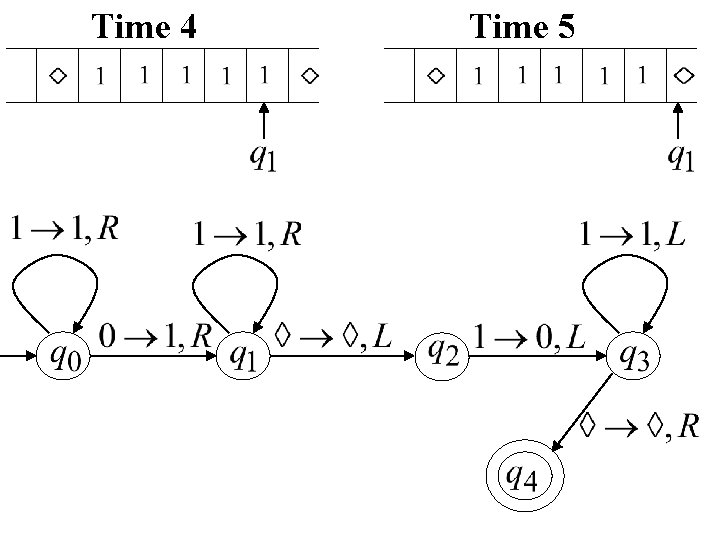
Time 4 Time 5

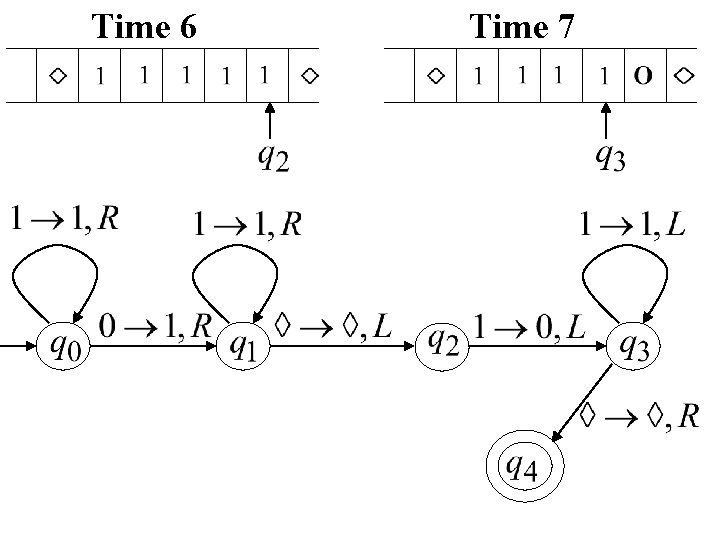
Time 6 Time 7

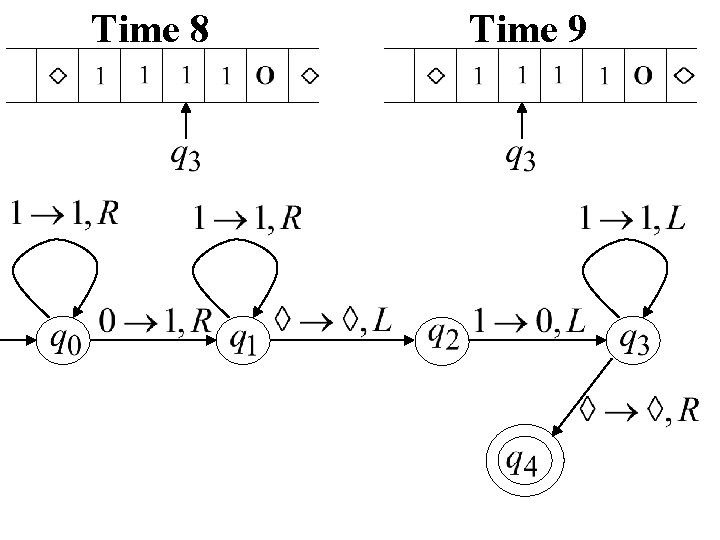
Time 8 Time 9

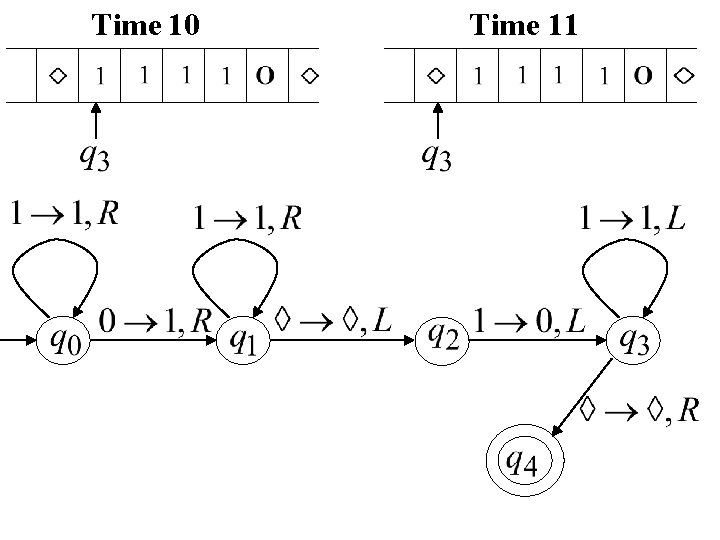
Time 10 Time 11

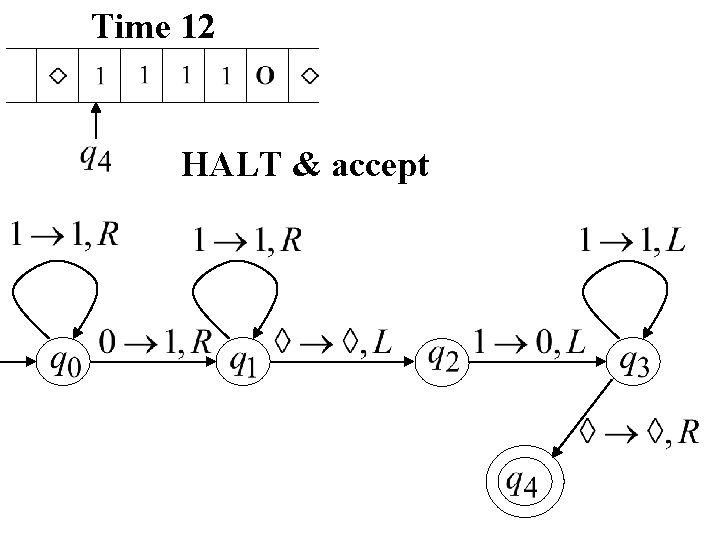
Time 12 HALT & accept

Try the following your self Draw a transition diagram for a TM that accepting each of the following languages a. b.

Computational Complexity

Measuring & Classifying Complexity

The complexity of computational problem can be on a certain machine as model of computation. TM will be selected as model of computation for specific problems need to be solved. Complexity of problem may be measured based on how much time and/or space machine required to solve the problem.

The Concept of “Complexity” The harder a problem, the more costly it is to solve: Time cost: number of steps required Space cost: maximum number of tape cells used

Time & Space Complexity of a TM. Whenever a TM solve a certain decidable problem, then it possible to measure the time (the number of moves) and the space (the number of tape squares/cells) needed for the computation. The most common approach of complexity is to consider the worst case: the maximum time or space that might be needed by any input string of a certain length.

Time & Space Complexity of a deterministic TM. Let T be a deterministic TM. The time complexity of T is the function τT defined on the natural numbers (N) as follows: τT(n) = max(number of steps/moves T can make on any input string of length n) Note: input string is assumed to be efficiently encoded

The space complexity of T is the function s. T defined on the natural numbers (N) as follows: s. T(n) = max(number of tape squares/cells used by T for any input string of length n) Which is greater – Time or Space? For every TM: Time complexity ≥ Space complexity . . . because it takes at least one step to write one cell on the tape

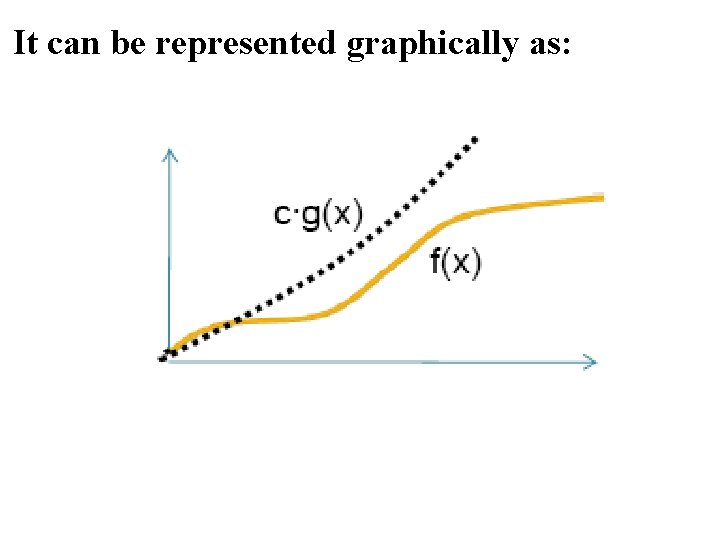
Expressing Complexity “big-Oh” notation will be used for expressing complexity e. g. “T’s time complexity (τT ) is O(n)” instead of “T's time complexity (τT ) = 2 n+1"

It can be represented graphically as:

Big O Notation “big-Oh” notation that used for measuring the running time taken by a TM to fully accept solving the problem and halts. Suppose the running time, τT = 6 n 3 + 2 n 2 + 20 n + 45, then τT = O(n 3), meaning that τT ≤ n 3 if disregarded the lower order terms and a constant factor. ◦ Bounds of the form nc for c > 0 are called polynomial bounds. ◦ Bounds of the form exponential bounds. δ) (n 2 for δ a real number > 0 are called

Does Complexity Class Matter? n log(n) 10 100 1, 000 3. 3 6. 6 10. 0 10, 000 13. 3 100, 000 16. 6 1, 000 19. 9 nlog(n) n 2 n 3 33. 2 664. 4 9965. 8 1000000 1000000 1 E+09 132877. 1 1. 66 E+06 1. 99 E+07 1 E+08 1 E+10 1 E+12 If 106 operations per second. . . s r u o h 8 7 2 s r a e y 0 0 32, 0 1 E+12 1 E+15 1 E+18

Example The time complexity for TM, T accepting the language: L(T) = { 0 k 1 k : k ≥ 0 } Cross off one 0 and one 1 each pass, τT = O(n 2) Cross off every other 0 and 1 each pass: τT = O(nlogn)

Complexity Classes: There are 3 important classes of problems: o. P: problems for which a deterministic polynomialtime solution exists o. NP: problems for which a nondeterministic polynomial-time solution exists o PSPACE: problems for which a deterministic polynomial-space solution exists o. These classes define the boundaries of what is considered to be tractable

The Class P ◦ Problems in P can be solved in polynomial time (therefore polynomial space) by a deterministic TM. ◦ Class P includes all and only those languages that are decidable by a deterministic single-tape Turing machine in polynomial time. i. e. P = TIME(nk) Examples ◦ Finding a name in a list – O(n)

The Class NP ◦ Problems in NP can be solved in polynomial time (and space) by a nondeterministic TM ◦ NP: "Nondeterministic Polynomial-time“ ◦ Class NP includes all and only those languages that nondeterministic are decidable Turing polynomial time. i. e. P = by machine NTIME(nk) a in

The Class NP –cont Two ways to understand this: ◦ Think of the NTM as executing all of its possible computations in parallel: Accept as soon as any of them accepts Reject when all of them reject ◦ Think of the NTM as "guessing" which a computation that will correctly accept, and carrying it out

The Class PSPACE Problems in PSPACE can be solved in polynomial space (but not necessarily polynomial time) by a deterministic TM ◦ PSPACE: "Polynomial space”

Complexity Class Relationships Clearly: P ⊂ NP ⊂ PSPACE �� Nobody knows whether the containment is proper That is, no one has ever been able to show there exists a problem in either NP – P or PSPACE – NP On the other hand, nobody has ever proved NP = P or NP = PSPACE!