Theory of Computation Pushdown Automata pda Lecture 11

Theory of Computation Pushdown Automata pda Lecture #11

PDA & Languages (CFL)

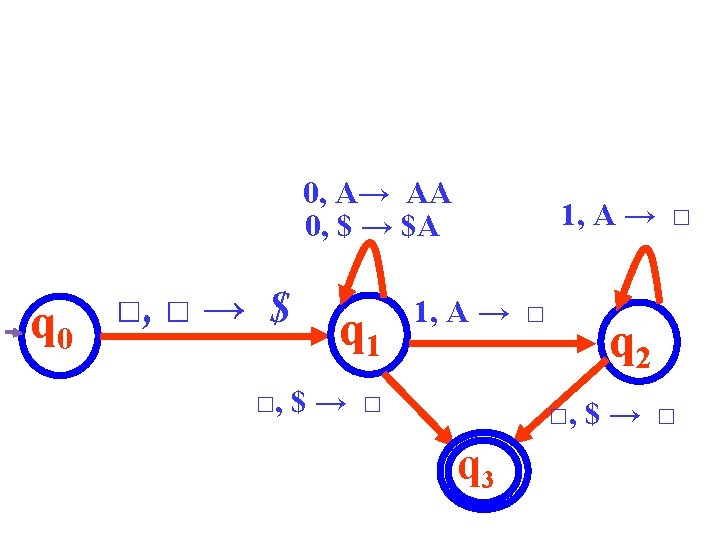
Example Design a PDA that accept the n n language L = {0 1 | n ≥ 0}. The PDA will be designed in the following way: • Machine begins with its input on the input tape and an empty stack. • The first thing the machine does is go from state q 0 to state q 1, pushing the bottom-of-the-stack marker onto the stack.

• In state q 1, if the machine reads an 0 from the input tape and pops the blank off the stack, then that is the first 0 found in the input and the machine pushes the blank back onto the stack followed by an A. • The machine counts the 0's in the input by pushing an A onto the stack for each 0 that it reads off the tape. • From this point on, if the PDA is in state q 1 and it finds an 0 in the input, there will be an A to top of the stack.

• The machine then pushes two A's back on the stack, one to make up for the A that was popped and one to count the 0 just found in the input. • As soon as the machine sees a 1 in the input it changes to state q 2 and pops an A off the stack. • It continues popping an A for each 1 that it finds. • If the input was a correctly formatted string, the machine will read a blank off the input tape at the same time that it pops a blank off the stack and go to state q 3, an accept state.

• Since the language includes the empty string, we also have a transition from state q 1 to state q 3 that is used if the machine reads a blank from the input at the same time as it pops the marker off the stack at the very beginning of processing. Based on this discussion a PDA, M = (Q, Σ, Γ, δ, Z, q, F) where, Q = {q 0, q 1, q 2, q 3}, Σ = {0, 1}, Γ = {$, A}, q 0 is the start state, F = {q 3}, and the transition function δ will be given by:

q 0 □ □ → q 1 R $, pushes $ onto the stack q 1 0 $ → q 1 R $A, pushes 0 onto the stack q 1 0 0 → q 1 R AA, pushes 0 onto the stack q 1 □ $ → q 3 N ε, input string is empty accepted q 1 1 A → q 2 R A, pop top symbol (0) form the stack q 2 1 A → q 2 R ε, pop top symbol (0) form the stack q 2 □ $ → q 3 N ε input string is empty accepted Then, the PDA state diagram can be shown as:

Another way to design the PDA is: The PDA, uses only two states: state q 0 and state q 1, where q 0 is the start state. Initially, the PDA will be in state q 0. 1. For each 0 that is read, the PDA pushes one symbol S onto the stack and stay in state q 0. 2. When the first 1 is read, then the PDA switches to state q 1, from that moment: - for each 1 that is read, the PDA pops the top symbol form the stack, and stay in q 1. - for each 0 that is read, the PDA doesn’t make any changes, and therefore doesn’t terminate.

Based on this discussion, a deterministic PDA, is M = (Q, Σ, Γ, δ, Z, q, F) where, Q = {q 0, q 1}, Σ = {0, 1}, Γ {$, S}, q 0 is the start state, F = {q 0, q 1}, and the transition function δ will be given by: q 0 0 $ → q 0 R $S, pushes S onto the stack q 0 0 S → q 0 R SS, pushes S onto the stack q 0 1 $ → q 0 N $, first symbol in the input is 1, loop forever q 0 1 S → q 1 R ε, first symbol 1, encountered q 0 □ $ → q 0 N ε, input string is empty accepted

q 0 □ S → q 0 N S, input consists only of 0’s; loop forever q 1 0 $ → q 1 N $, 0 to the right of 1; loop forever q 1 0 S → q 1 N S, 0 to the right of 1; loop forever q 1 1$ → q 1 N $, too many 1’s; loop forever q 1 1 S → q 1 R ε, pop top symbol form the stack q 1 □ $ → q 1 N ε, input string is empty accepted

DPDA Let M = (Q, Σ, Γ, δ, q, Z, F) be a pda. M will be deterministic if there is no configuration for which M ha a choice of more that one move. In other words M is deterministic if there are no choices: § Depends on a state’s (input symbol, pop symbol) pair: 1. δ(q, a, X) has only one choice (a could be ε), and 2. if a is not ε, then there is no δ(q, ε, X) edge, and 3. if X is not ε, then there is no δ(q, a, ε) edge. Note: a language that accepted dpda is considered to be DCFL.

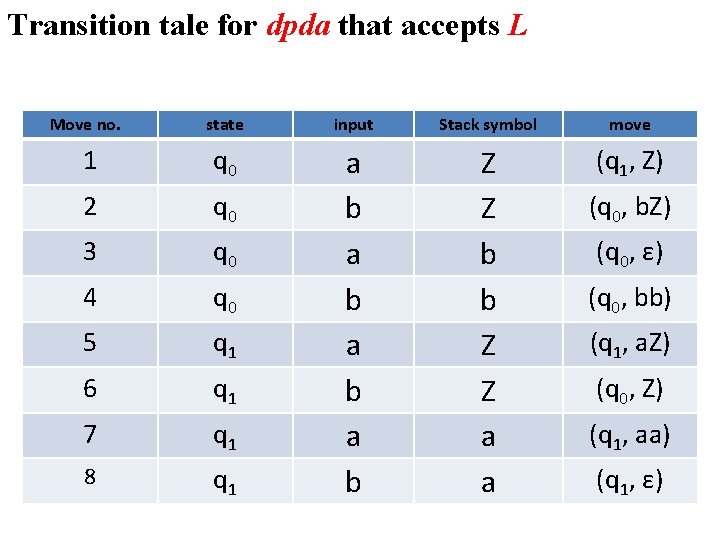
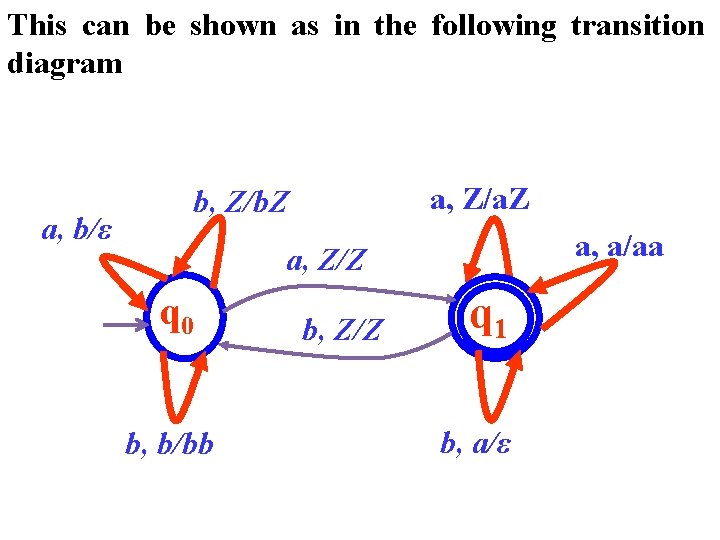
Example Design a dpda that accept the language L = {x ϵ {a, b}* | na(x) > nb(x)} Sol: M can be designed based on the following configuration using the transition table as follows:

Transition tale for dpda that accepts L Move no. state input Stack symbol move 1 q 0 3 q 0 4 q 0 5 q 1 6 q 1 7 q 1 8 q 1 Z Z b b Z Z a a (q 1, Z) 2 a b a b (q 0, b. Z) (q 0, ε) (q 0, bb) (q 1, a. Z) (q 0, Z) (q 1, aa) (q 1, ε)

This can be shown as in the following transition diagram a, b/ε a, Z/a. Z b, Z/b. Z a, a/aa a, Z/Z q 0 b, b/bb b, Z/Z q 1 b, a/ε

NPDA The NPDA model is similar to the PDA, where it 7 -tuples, M = (Q, Σ, Γ, δ, q, Z, F). The difference is that, the next computation step may not be uniquely defined. The automata can make out a choice of a finite number of possible transitions. In this case the transition function δ is given by: δ : Q (Σ {□} {ε}) Γ → Pj(Q {R, N} Γ*) Where Pj(K) is the set of all finite subsets of the set K

states Q is a finite set of Σ is the set of input alphabet Г is the stack alphabet q 0 Q is the initial state Z is the stack start symbol , and F Q is a set of final states

Same as the PDA, the language L is said to be accepted by the NPDA if all strings in Σ* performing L are accepted/recognized by M, and it is represented as L(M).

DPDA vs. NPDA • Deterministic PDA’s – Every state/stack combination has exactly one transition – No ε-transitions (ε for both input and stack symbol) • NPDA’s are more powerful than DPDA’s – Example: strings from a*b* that have either twice as many a’s as b’s or 3 x as many a’s as b’s

Example: consider the following grammar S 0 S 0 | 1 S 1 | ε Design a suitable pda that recognize the language generated by the given grammar

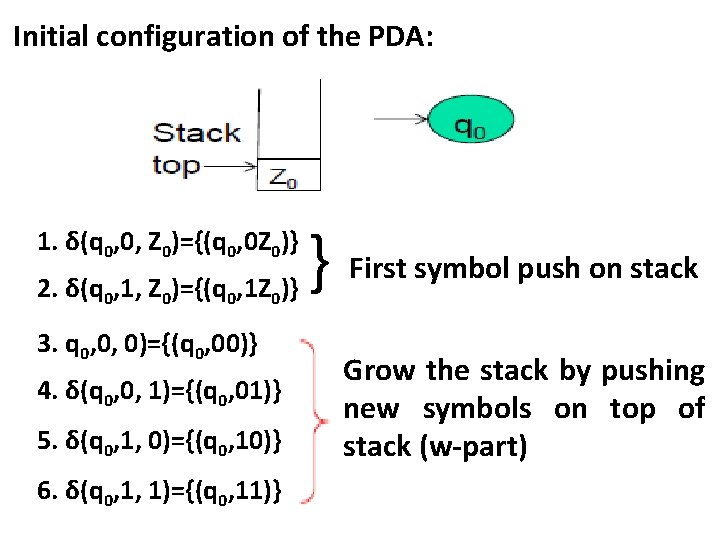
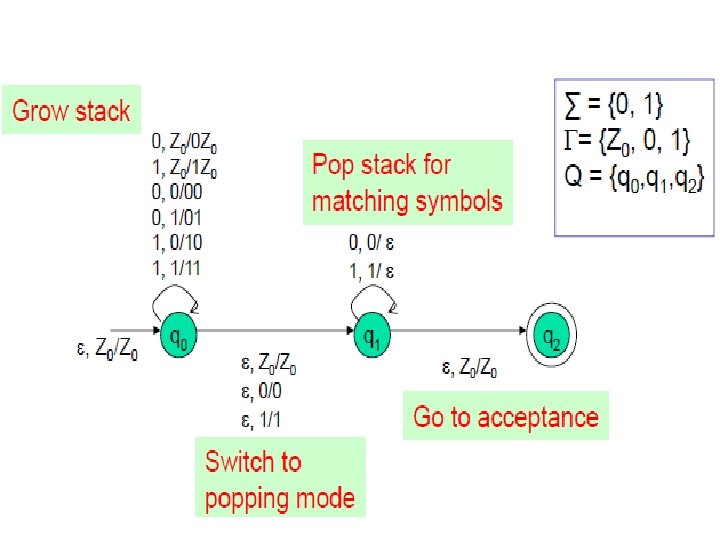
r L = {ww | w ϵ(0+1)*} The pda can be design based on the following model: P : = ( Q, Σ, Γ, δ, q 0, Z 0, F ) = ( {q 0, q 1, q 2}, {0, 1, Z 0}, δ, q 0, Z 0, {q 2}) The model construction can be illustrated as follow: (nondeterministic)

Initial configuration of the PDA: 1. δ(q 0, 0, Z 0)={(q 0, 0 Z 0)} 2. δ(q 0, 1, Z 0)={(q 0, 1 Z 0)} 3. q 0, 0, 0)={(q 0, 00)} 4. δ(q 0, 0, 1)={(q 0, 01)} 5. δ(q 0, 1, 0)={(q 0, 10)} 6. δ(q 0, 1, 1)={(q 0, 11)} } First symbol push on stack Grow the stack by pushing new symbols on top of stack (w-part)

7. δ(q 0, ε, 0)={(q 1, 0)} 8. δ(q 0, ε, 1)={(q 1, 1)} 9. δ(q 0, ε, Z 0)={(q 1 Z 0)} 10. δ(q 1, 0, 0)={(q 1, ε)} 11. δ(q 1, 1, 1)={(q 1, ε)} Switch to popping mode, nondeterministically (boundary between w and wr ) Shrink the stack by popping matching symbols (wr-part) 12. δ(q 1, ε, Z 0)={(q 2, Z 0)} Enter acceptance state So, the pda as a state diagram as npda can be shown as follows:

Example Design an NPDA, that can be used to recognized/accept the following language L, where L(M) = {vbw : v, w {a, b}*, |v| = |w|}. Sol. The NPDA, can be designed based on two states (q 0 as start state and q 1 as accepting state) with following meaning:

• If the NPDA at state q 0, then it hasn’t reached the middle symbol of the input string. • If the NPDA at state q 1, then it has already reached the middle symbol of the input string. Since the automata makes only one single pass over the input string, it has to guess (nondeterminism) when it reaches the middle of the string.

• At state q 0, when reading the current input symbol, it performs: - pushes one symbol S onto stake and stay in the same state, or - in case current input symbol is b is guess it has reached to middle of the string and switches to state q 1 • At state q 1, when reading the current input symbol, it pops symbol S from the top of the stack and stay at the state. • Then string will be accepted when stack is empty for the first time after the entire input string has been read and machine switches to q 2.

Based on this discussion a NPDA, M = (Q, Σ, Γ, δ, q, F) where, Q = {q 0, q 1, q 2}, Σ = {a, b}, Γ {$, A}, q 0 is the start state, F = {q 2}, and, the transition function δ will be given by:

q 0 a $ → q 0 R $S, pushes S onto the stack q 0 a S → q 0 R SS, pushes S onto the stack q 0 b $ → q 1 R $, reached the middle (guess) q 0 b S → q 0 R $S, not reached the middle q 0 b S → q 1 R S, reached the middle (guess) q 0 b S → q 0 R SS, not reached the middle q 0 □ $ → q 0 N $, loop forever q 0 □ S → q 0 N S, loop forever q 1 a $ → q 1 N ε, empty stack, terminate, rejected q 1 a S → q 1 R ε q 1 b $ → q 1 N ε, empty stack, terminate, rejected q 1 b S → q 1 R ε

q 1 □ $ → q 2 N ε, input accepted q 1 □ $ → q 1 N S, loop forever For more details and examples on pda (dpda or npda) you can refer to the mentioned references.