Theory of Computation ContextFree Languages Last Time Is

Theory of Computation Context-Free Languages

Last Time • Is L = {0 ix | i ≥ 0, x {0, 1}* and |x| ≤ i} regular? • Is L = {0 i | i is prime} regular? Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Context-Free Languages • Context-Free Languages (CFL) are described using Context-Free Grammars (CFG). • A CFG is a simple recursive method of specifying grammar rules which can generate strings in a language – these languages are the CFL’s. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Context-Free Grammars • The following is an example of a CFG, call it G 1: – A → 1 A 0 –A→B –B→# (A and B = variables) (0, 1 and # = terminals) • A grammar consists of a collection of substitution rules (projections). • A is start variable in this case – usually occurs on left hand side of topmost rule. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Context-Free Grammars • Use grammar to describe a language by generating each string of language: – Write down start variable. – Find a variable and a rule which starts with that variable. Replace written variable with the right hand side of this rule. – Repeat the second step until no variables remain. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Context-Free Grammars • G 1 generates the string 1111#0000 using the following sequences: • A → 1 A 0 → 11 A 00 → 111 A 000 → 1111 A 0000 → 1111 B 0000 → 1111#0000 Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Context-Free Grammars • All strings generated in this manner constitute the language of the grammar. • L(G 1) = language of grammar G 1. • Can show that L(G 1) is {1 n#0 n | n ≥ 0}. • Any language that can be generated by some context-free grammar is called a context-free language. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Context-Free Grammars • Note: – For convenience if a variable has several rules they are often abbreviated: – A → 1 A 0 and A → B may be represented as: A → 1 A 0 | B, where “|” represents “or”. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Definition of a CFG • A context-free grammar is a 4 -tuple (V, Σ , R, S), where – – V are the variables (finite set) Σ are the terminal states (finite set) R is the set of rules S is the start variable, S V Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Context-Free Grammars • In grammar G 1, V = {A, B}, Σ = {0, 1, #}, S = A, and R is the collections of the rules: – A → 1 A 0 –A→B –B→# Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Context-Free Grammars • Consider G 3 = ({S}, {a, b}, R, S). The set of rules R, is • S → a. Sb | SS | ε • This grammar generates strings such as ab, abab, aababb and aaabbb. • Note that L(G 3) is the language of all strings of properly nested parnetheses. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Context-Free Grammars • Consider the language of palindromes: – L = {w {a, b}* | w = wr} • This is not regular, but the language can be generated by the following rules: – S → a. Sa S → b. Sb S→ a S→b S→ε • V = {S}, S = S, Σ = {a, b} and R are rules above. • Check to ensure if produces palindromes. • What about a CFG for the non-palindromes? Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

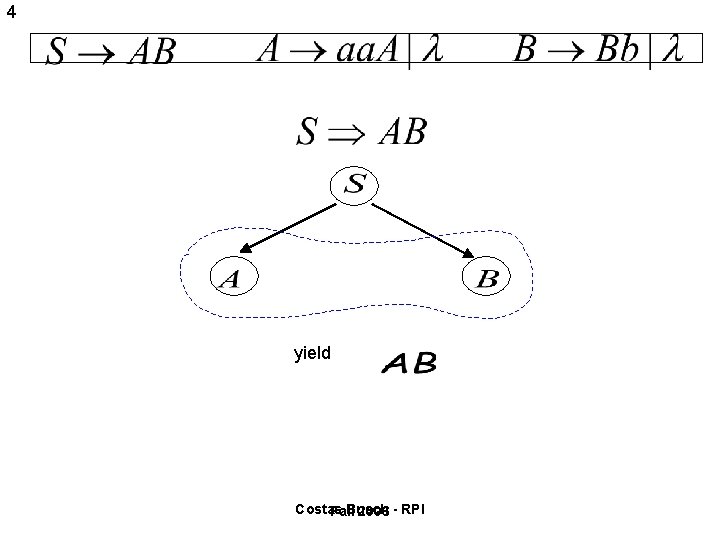
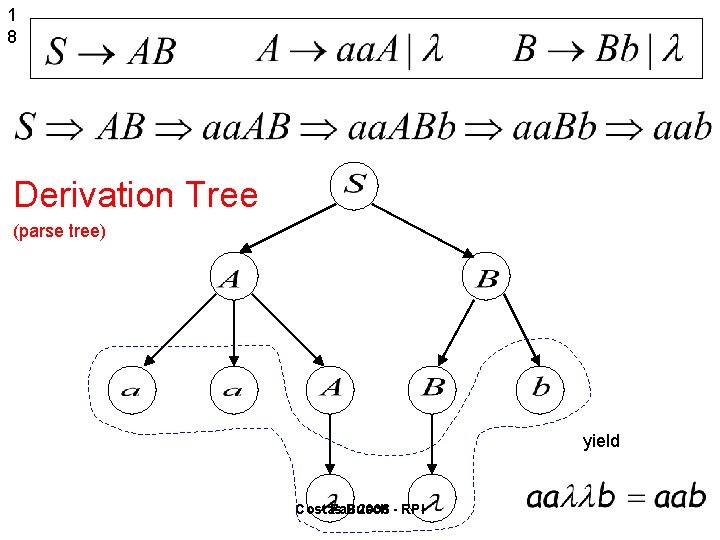
3 Derivation Trees Consider the same example grammar: And a derivation of : Costas Busch Fall 2006 - RPI

4 yield Costas Busch Fall 2006 - RPI

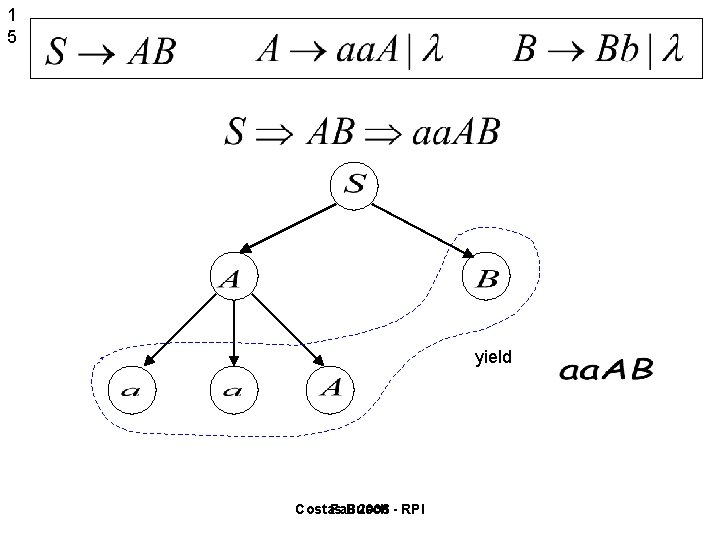
1 5 yield Costas Fall Busch 2006 - RPI

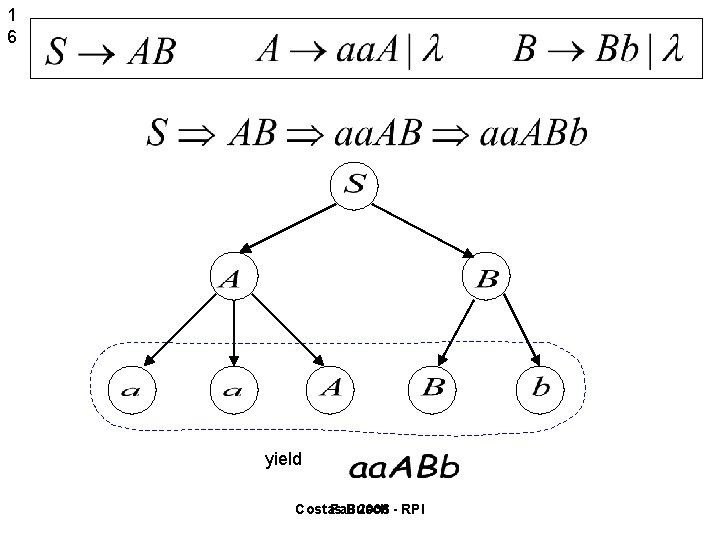
1 6 yield Costas Fall Busch 2006 - RPI

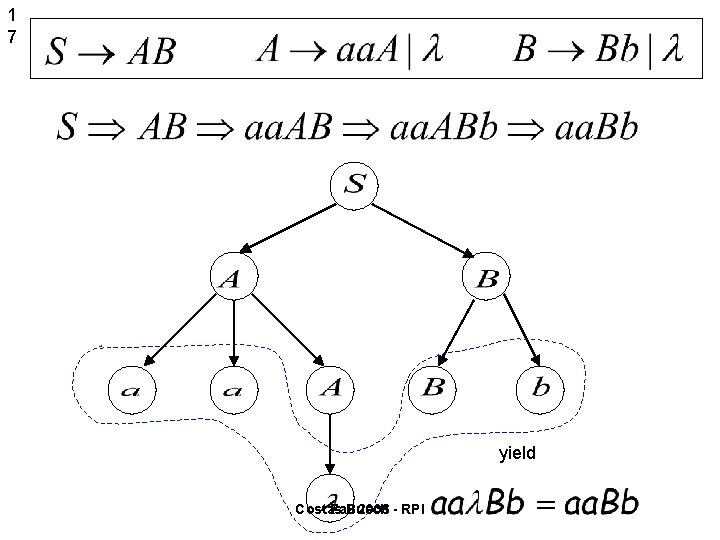
1 7 yield Costas Fall Busch 2006 - RPI

1 8 Derivation Tree (parse tree) yield Costas Fall Busch 2006 - RPI

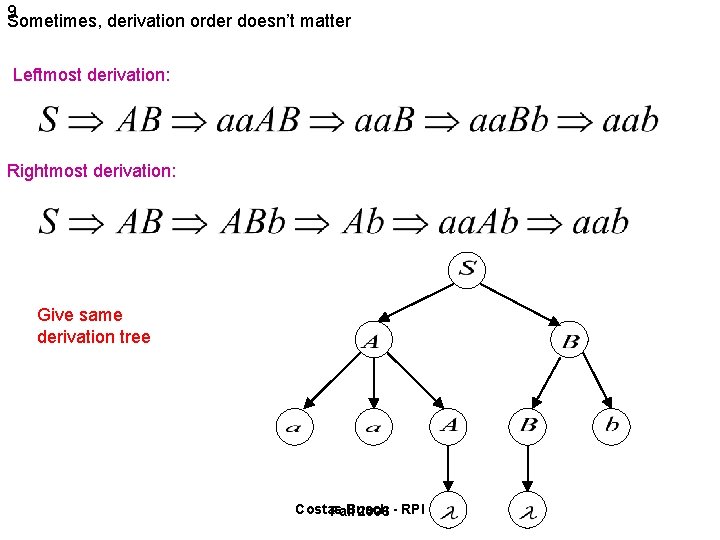
9 Sometimes, derivation order doesn’t matter Leftmost derivation: • Rightmost derivation: Give same derivation tree Costas Busch Fall 2006 - RPI

Designing CFG’s • Many CFL’s are the union of simpler ones. • Construct the smaller simpler CFG’s and then construct them to give the larger CFG for the CFL. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Designing CFG’s • Construct a grammar for the language: {0 n 1 n | n ≥ 0} {1 n 0 n | n ≥ 0}. • Firstly construct the grammar • S 1 → 0 S 11 | ε for the language {0 n 1 n | n ≥ 0}, and the grammar • S 2 → 1 S 20 | ε for the language {1 n 0 n | n ≥ 0}, and then add the rule S → S 1| S 2 to give the grammar: – S → S 1| S 2 – S 1 → 0 S 11 | ε – S 2 → 1 S 20 | ε Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Designing CFG’s • We can construct a CFG for a regular language by first constructing a DFA for the language. • A DFA may be converted into an equivalent CFG as follows: • Make a variable Ri for each state qi of the DFA. • Add the rule Ri → a. Rj to the CFG if δ(qi, a) = qj is a transition in the DFA. • Add the rule Ri → ε if qi is an accept state of the DFA. • Make R 0 the start state of the grammar where q 0 is the start state of the machine. • Verify that it works!! Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Union, concatenation and closure of CFG’s • Theorem: If L 1 and L 2 are CFL’s then L 1 L 2, L 1 L 2 and L*1 are also CFL’s. • That is, the context-free languages are closed under union, concatenation and Kleene-closure. • The proofs are constructive. • Begin with two grammars: G 1 = (V 1, Σ , R 1, S 1) and G 2 = (V 2, Σ , R 2, S 2), generating CFL’s L 1 and L 2 respectively. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Union of CFG’s • The new CFG Gx is made as: – – Σ remains the same Sx is the new start variable Vx = V 1 V 2 {Sx} Rx = R 1 R 2 {Sx → S 1|S 2} • Explanation: All we have done is augment the variable set with a new start state and then allowed the new start state to map to either of the two grammars. So, we’ll generate strings from either L 1 or L 2, i. e. L 1 L 2 Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Concatenation of CFG’s • The new CFG Gy is made as: – – Σ remains the same Sy is the new start variable Vy = V 1 V 2 {Sy} Ry = R 1 R 2 {Sx → S 1 S 2} • Explanation: Again, all we have done is to augment the variable set with a new start state, and then allowed the new start state to map to the concatenation of the two original start symbols. So, we will generate strings that begin with strings from L 1 and end with strings from L 2, i. e. L 1 L 2 Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Kleene-Closure of CFG’s • The new CFG Gz is made as: – – Σ remains the same Sz is the new start variable Vz = V 1 {Sz} Rz = R 1 {Sz → S 1 Sz | ε} • Explanation: Again we have augmented the variable set with a new start state, and then allowed the new start state to map to either S 1 Sz or ε. This means we can generate strings with zero or more strings made from expanding the variable S 1, i. e. L*1 Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

7 2 0 0 6 Ambiguity Costas Busch - RPI

2 8 Grammar for mathematical expressions Example strings: Denotes any number Costas Fall Busch 2006 - RPI

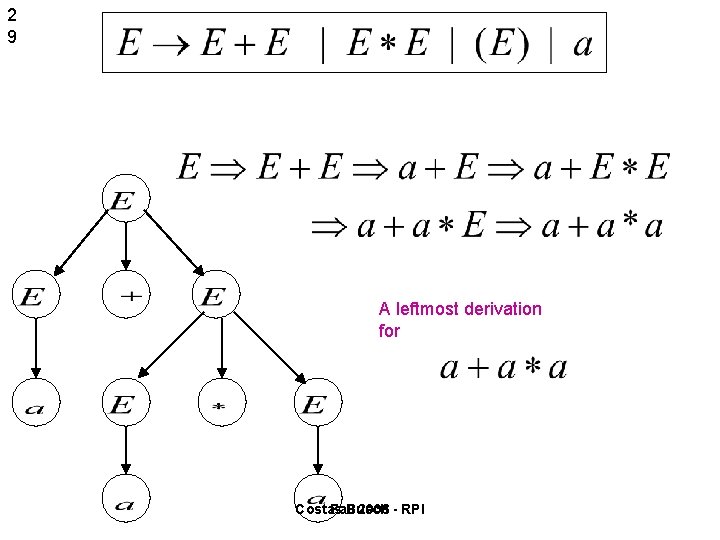
2 9 A leftmost derivation for Costas Fall Busch 2006 - RPI

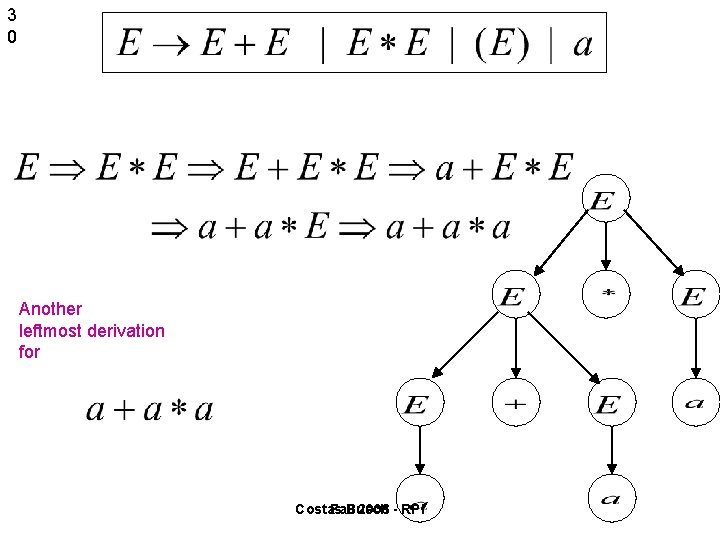
3 0 Another leftmost derivation for Costas Fall Busch 2006 - RPI

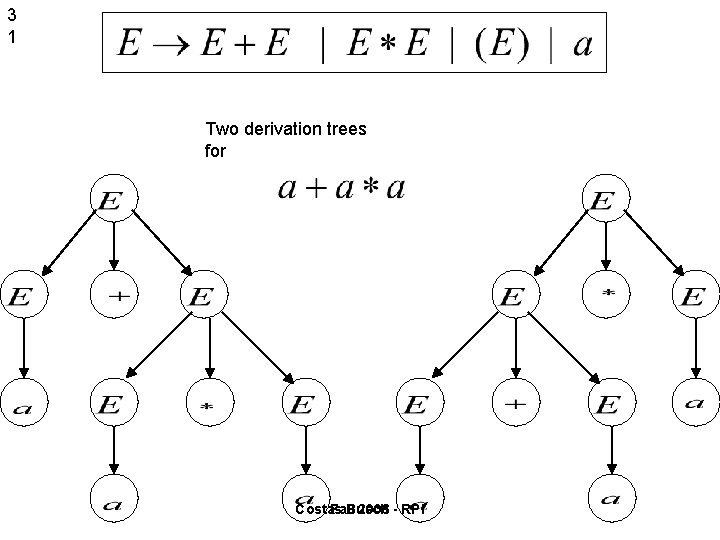
3 1 Two derivation trees for Costas Fall Busch 2006 - RPI

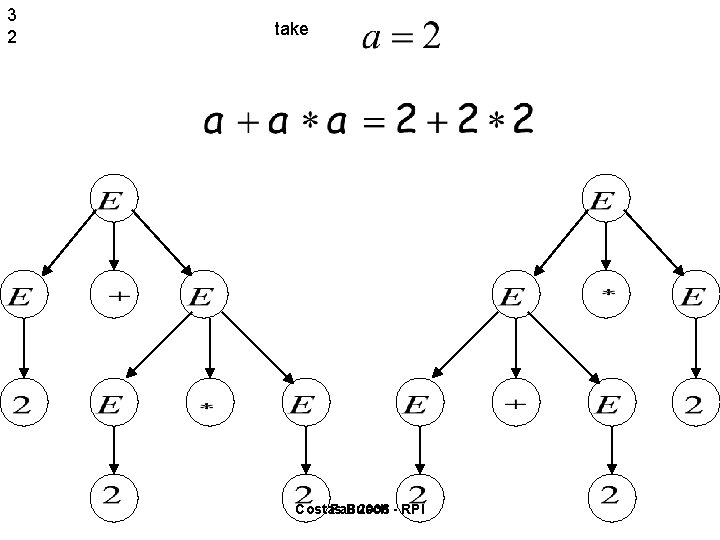
3 2 take Costas Fall Busch 2006 - RPI

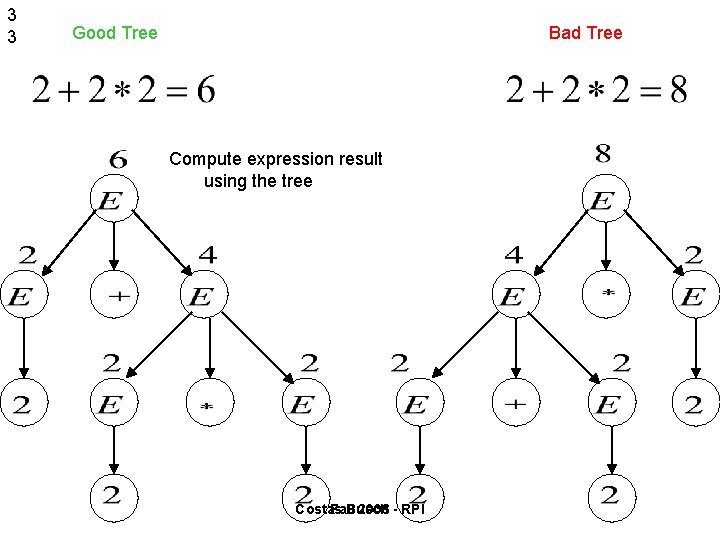
3 3 Good Tree Bad Tree Compute expression result using the tree Costas Fall Busch 2006 - RPI

3 4 Two different derivation trees may cause problems in applications which use the derivation trees: • Evaluating expressions • In general, in compilers for programming languages Costas Fall Busch 2006 - RPI

3 5 Ambiguous Grammar: A context-free grammar if there is a string is ambiguous which has: two different derivation trees or two leftmost derivations (Two different derivation trees give two different leftmost derivations and vice-versa) Costas Fall Busch 2006 - RPI

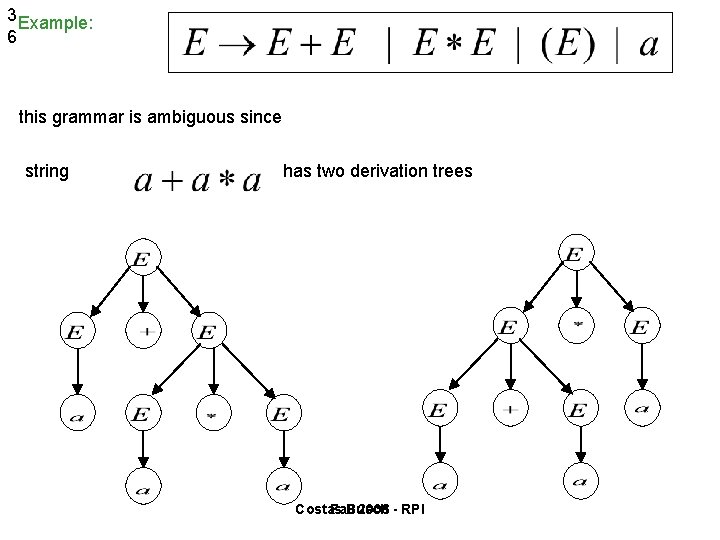
3 Example: 6 this grammar is ambiguous since string has two derivation trees Costas Fall Busch 2006 - RPI

3 7 this grammar is ambiguous also because string has two leftmost derivations Costas Fall Busch 2006 - RPI

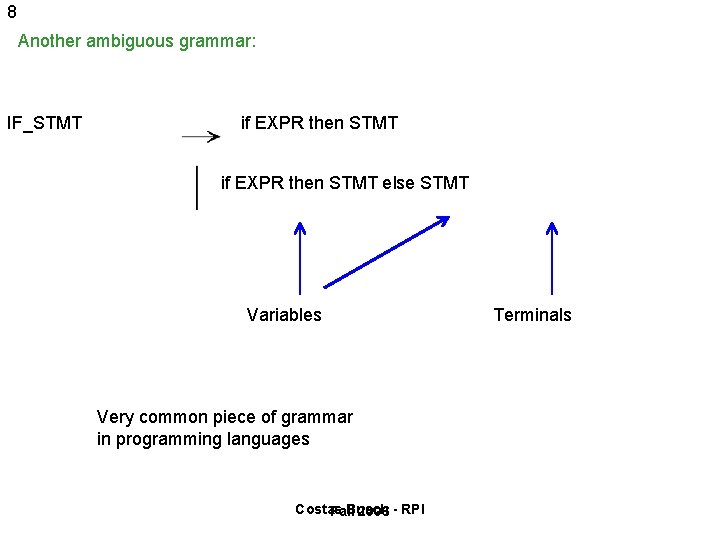
8 Another ambiguous grammar: IF_STMT if EXPR then STMT else STMT Variables Very common piece of grammar in programming languages Costas Busch Fall 2006 - RPI Terminals

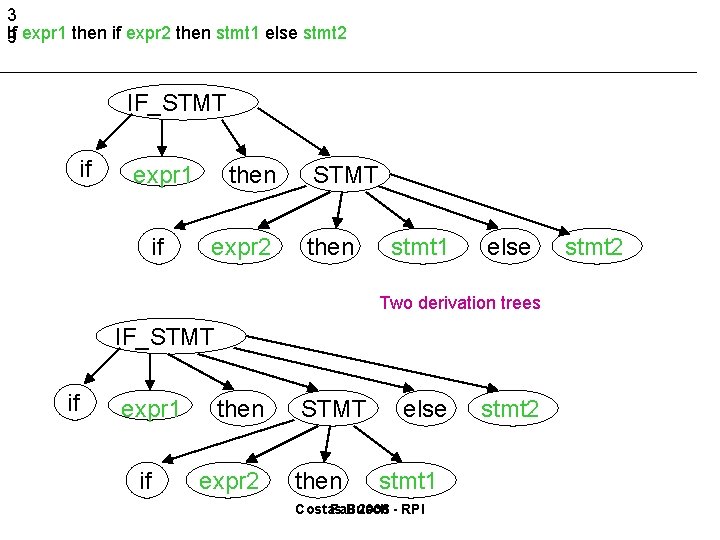
3 If expr 1 then if expr 2 then stmt 1 else stmt 2 9 IF_STMT if expr 1 if then expr 2 STMT then stmt 1 else Two derivation trees IF_STMT if expr 1 if then expr 2 STMT then else stmt 1 Costas Fall Busch 2006 - RPI stmt 2

4 0 In general, ambiguity is bad and we want to remove it Sometimes it is possible to find a non-ambiguous grammar for a language But, in general we cannot do so Costas Fall Busch 2006 - RPI

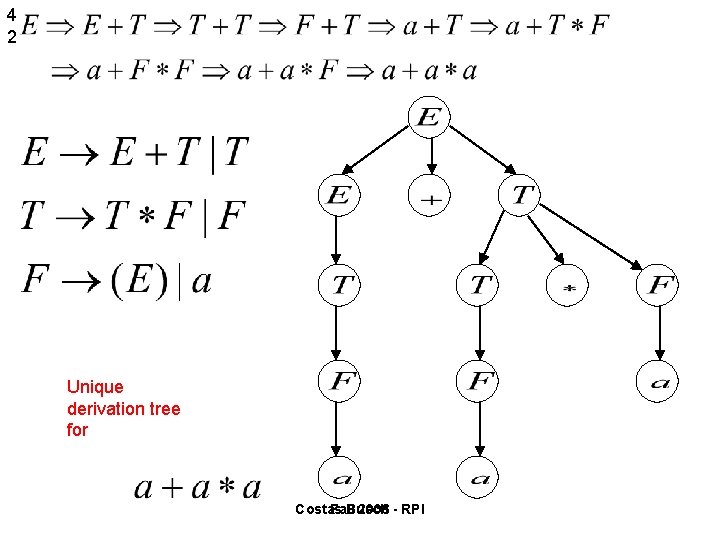
4 1 A successful example: Equivalent Ambiguous Grammar Non-Ambiguous Grammar generates the same language Costas Fall Busch 2006 - RPI

4 2 Unique derivation tree for Costas Fall Busch 2006 - RPI

3 An un-successful example: is inherently ambiguous: every grammar that generates this language is ambiguous Costas Busch Fall 2006 - RPI

4 Example (ambiguous) grammar for : Costas Busch Fall 2006 - RPI

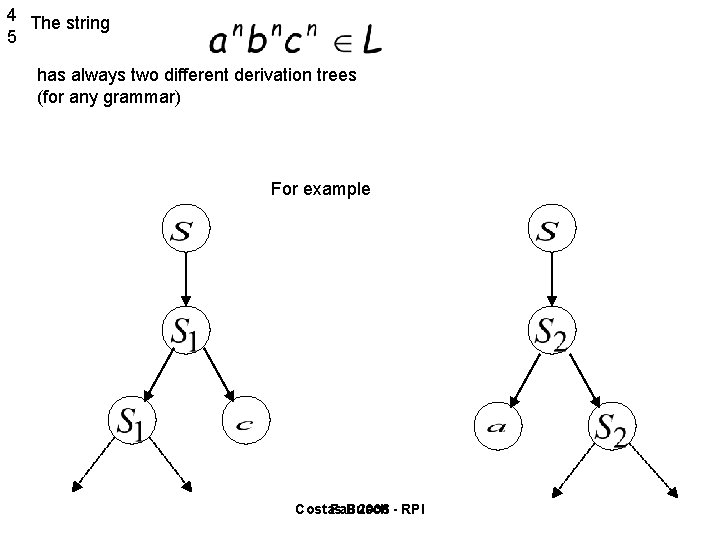
4 The string 5 has always two different derivation trees (for any grammar) For example Costas Fall Busch 2006 - RPI

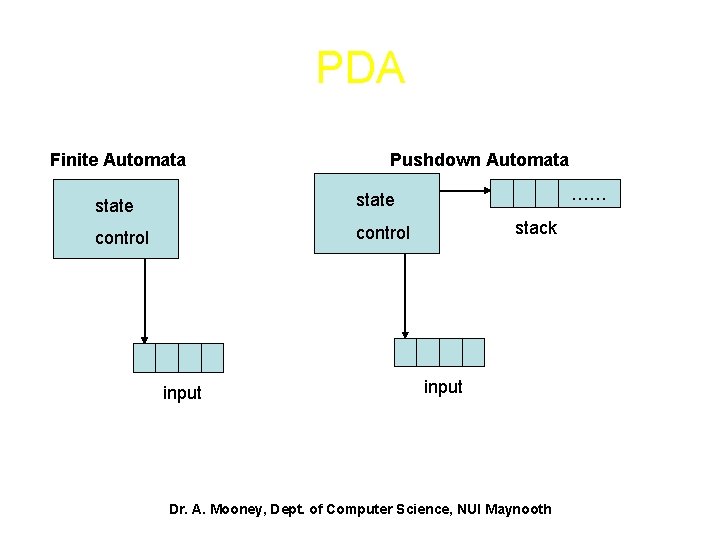
Pushdown Automata (PDA) • Pushdown Automata are similar to nondeterministic finite automata but have an extra element – stack. • This stack provided extra memory space. • Also allows pushdown automata to recognise some nonregular languages. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

PDA Finite Automata Pushdown Automata state control input …… stack input Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

PDA • Why is a stack useful? – It can hold an unlimited amount of information. • Remember that a FA was unable to recognise the language {0 n 1 n | n ≥ 0} because it can’t store large numbers. • However, a PDA does not have this problem, due to the presence of a stack: it can use the stack to store how many 0’s it has seen. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

PDA • A PDA can write symbols on the stack and read them back later. • Writing a symbol “pushes down” all the other symbols on the stack. • Only the top symbol in the stack can ever be read – once read it is removed. • Writing a symbol is known as “pushing” and reading a symbol known as “popping”. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

PDA • The PDA has no way of checking for an empty stack. • Gets around this by placing a special character, $, on the stack initially. • Then if it ever sees the $ again it knows that the stack is effectively empty. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

PDA • Important: • Deterministic and non-deterministic PDA’s are not equivalent in power. • Non deterministic PDA’s recognise certain languages which no deterministic pushdown automata can recognise. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Formal Definition of PDA’s • The formal definition of a PDA is similar to that of a FA, except for the stack. • The stack contains symbols drawn from some alphabet. • The machine may use different alphabets for its input and the stack – We need to specify an input alphabet Σ and a stack alphabet Γ Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Formal Definition of PDA’s • In order to formally define a PDA we need to determine the transition function. Recall: – Σε = Σ {ε} and Γε = Γ {ε} – The domain of the transition function is Q × Σε × Γε • Therefore, the current state, next input symbol read and top state of the stack determine the next move of the PDA. • Note that either symbol may be ε meaning that the machine may move without reading a symbol from the input or the stack. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Formal Definition of PDA’s • What is the range of the transition function? • The machine may enter some new state and possibly write to the top of the stack. • The function δ can represent this by returning a member of Q along with a member of Γε, i. e. a member of Q × Γε • A number of legal next moves may be allowed – The transition function incorporates this nondeterminism in the usual way – i. e. returning a set of members of Q × Γε, that is, a member of P(Q × Γε). Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Formal Definition of PDA’s • A pushdown automata is a 6 -tuple (Q, Σ, Γ, δ, q 0, F), where Q, Σ, Γ, and F are all finite sets, and – Q is the set of states, – Σ is the input alphabet, – Γ is the stack alphabet, – δ: Q×Σε×Γε → P(Q × Γε) is the transition function, – q 0 –F Q is the start state, and Q is the set of accept states. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

PDA • The computation of a PDA, M, is as follows: – It accepts input w if w can be written as w = w 1 w 2…wm where each w 1 Σε and sequences of states r 0, r 1, …, rm Q and strings s 0, s 1, …, sm Γ* exist that satisfy the following: • r 0 = q 0 and s 0 = ε: M starts out properly, in start state and empty stack. • For i = 0, 1, . . , m-1, we have (ri+1, b) δ(ri, wi+1, a), where si = at and si+1 = bt for some a, b Γε and t Γ*: M moves properly according to the state, stack and next input symbols. • rm F: Accept states occurs when the input end is reached. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

PDA • In a state transition we write “a, b → c” to signify that when machine reads input a it may replace symbol b on top of the stack with a c. • Any of a, b, c can be ε. • If a is ε, the machine may make this transition without reading any input symbol. • If b is ε the machine performs transition without reading and popping any stack symbol. • If c is ε machine does not write any symbol to stack. • Can we design a PDA to recognise the language: {0 n 1 n | n ≥ 0} ? Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Context Free • A language is context free if and only if some pushdown automata recognises it. • Every regular language is recognised by a finite automaton and every finite automaton is automatically a pushdown automaton that ignores the stack, we can note that every regular language is also a context-free language. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Regular and Context-Free Languages Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Non-Context Free Languages • Recall that we looked at the pumping lemma previously for showing that certain languages are not regular. • We will look at a similar lemma for contextfree languages. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Pumping Lemma • The pumping lemma states that every contextfree language has a special value called the pumping length such that all longer strings in the language can be “pumped”. • Pumped, this time, means that the string can be divided into five parts such that the 2 nd and 4 th parts of the string may be repeated together any number of times and the resulting string still be part of the language. Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Pumping Lemma • If A is a context-free language, then there is a number p (the pumping length) where, if s is a string in A of length at least p, then s may be divided into 5 parts, s = uvxyz such that: – for each i ≥ 0, uvixyiz – |vy| > 0, and – |vxy| ≤ p. A Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth

Pumping Lemma • Let us look at some examples: – Use the Pumping Lemma to show that the following languages are not context-free: • • B = {anbncn | n ≥ 0} C = {aibjck | 0 ≤ i ≤ j ≤ k} D = {ww | w {0, 1}* } E = {0 n 1 n | n ≥ 0} Dr. A. Mooney, Dept. of Computer Science, NUI Maynooth