Theory of Bending Beams are subjected to bending

Theory of Bending • Beams are subjected to bending moment and shearing forces which vary from section to section. • To resist the bending moment and shearing force, the beam section develops stresses. • Bending is usually associated with shear. However, for simplicity we neglect effect of shear • and consider moment alone to find the stresses due to bending. • Such theory is known as PURE Bending

Example of Pure Bending

Bending Action Sagging: �Fibers are under tension at bottom �Fibers are in compression at top Neutral Axis: In between there is a fiber or layer which neither undergoes tension nor compression. This layer is called Neutral Layer (stresses are zero) and trace of this layer on the c/s is called the Neutral Axis.

Assumptions in simple bending �A transverse section of the beam, which was a plane before bending is symmetrical about the plane of bending. � Each cross-section of the beam is symmetrical about the plane of bending. � The material of the beam is homogeneous and � The beam material obey’s Hooke’s law. � The value of Young’s modulus of elasticity is the same in tension and compression. � The radius, of curvature of the beam before bending is very large as compared to the transverse dimensions of the beam. � Each layer of the beam is free to expand or contract, independently, of the layer, above or below it.

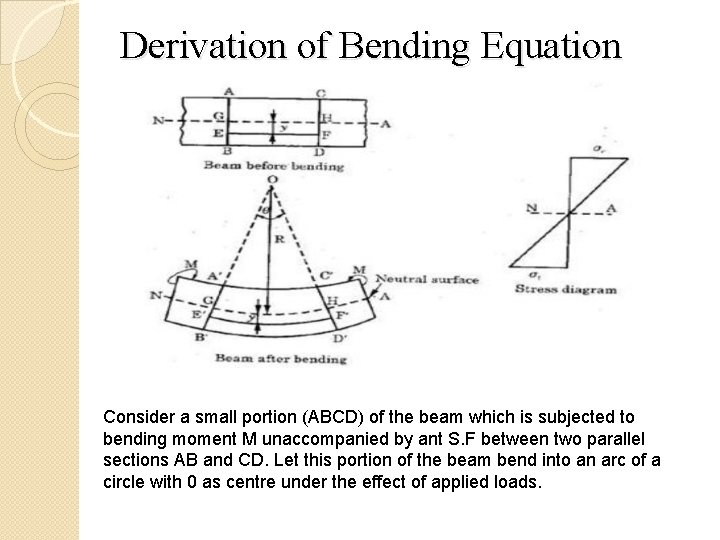
Derivation of Bending Equation Consider a small portion (ABCD) of the beam which is subjected to bending moment M unaccompanied by ant S. F between two parallel sections AB and CD. Let this portion of the beam bend into an arc of a circle with 0 as centre under the effect of applied loads.

� Fibers above neutral axis will be under compression and fibers below neutral axis will be under tension. � Consider a layer EF at a distance ‘y’ from neutral axis. After deformation EF will become E’F’ � Change in length of the fiber EF= E’F’-EF = (R+y) Ө RӨ=yӨ

� Hence, stress in any fibre is proportional to the distance of the fibre from the neutral axis. � Maximum bending stress of opposite nature will be at extreme fibres on both sides of the neutral axis.

Integrating the total area, we will get the moment of inertia of the section � Hence the equation is written as � � Combining the equations we get final as