Theory for Coordinating Hierarchical Planning Agents Using Summary

Theory for Coordinating Hierarchical Planning Agents Using Summary Information Brad Clement and Ed Durfee Artificial Intelligence Laboratory University of Michigan {bradc, durfee}@umich. edu

Multi-level Coordination & Planning A DA B DB blocked A DA B DB temporal constraints

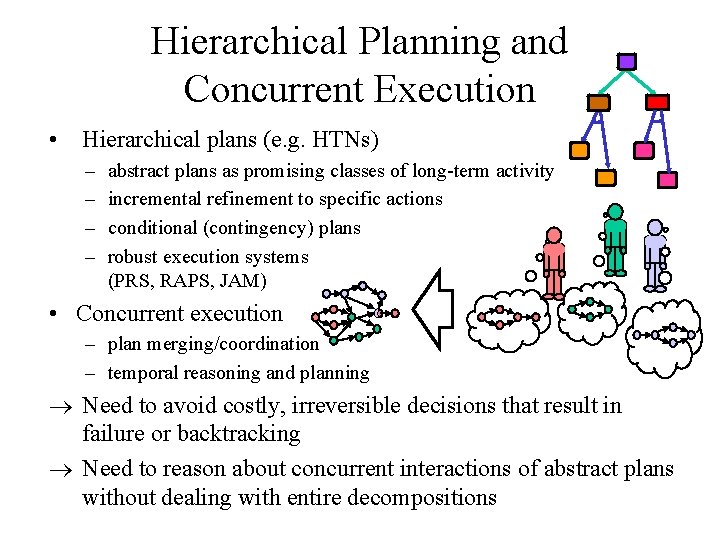
Hierarchical Planning and Concurrent Execution • Hierarchical plans (e. g. HTNs) – – abstract plans as promising classes of long-term activity incremental refinement to specific actions conditional (contingency) plans robust execution systems (PRS, RAPS, JAM) • Concurrent execution – plan merging/coordination – temporal reasoning and planning Need to avoid costly, irreversible decisions that result in failure or backtracking Need to reason about concurrent interactions of abstract plans without dealing with entire decompositions

Interleaving Planning, Execution, and Coordination • Reason about plans at abstract levels in order to make safe decisions and avoid backtracking summarize conditions for potential decompositions develop mechanisms for determining how plans can might interact coordinate hierarchical plans at abstract levels commit to safe abstract plans, refine, and execute o

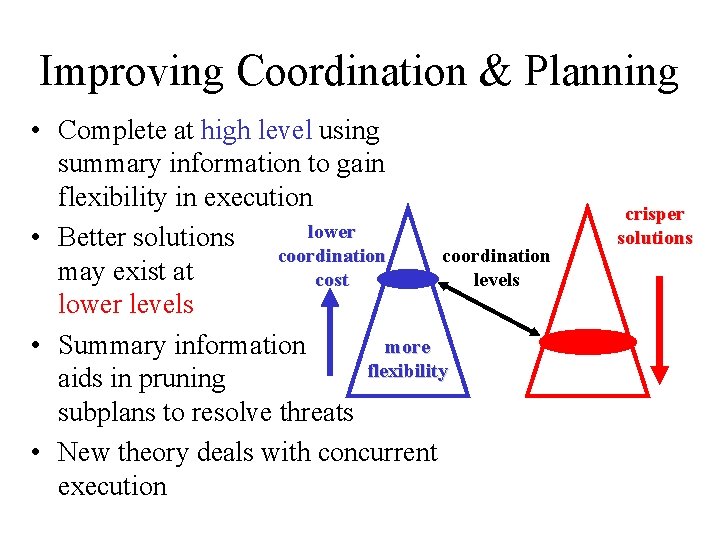
Improving Coordination & Planning • Complete at high level using summary information to gain flexibility in execution lower • Better solutions coordination may exist at cost levels lower levels more • Summary information flexibility aids in pruning subplans to resolve threats • New theory deals with concurrent execution crisper solutions

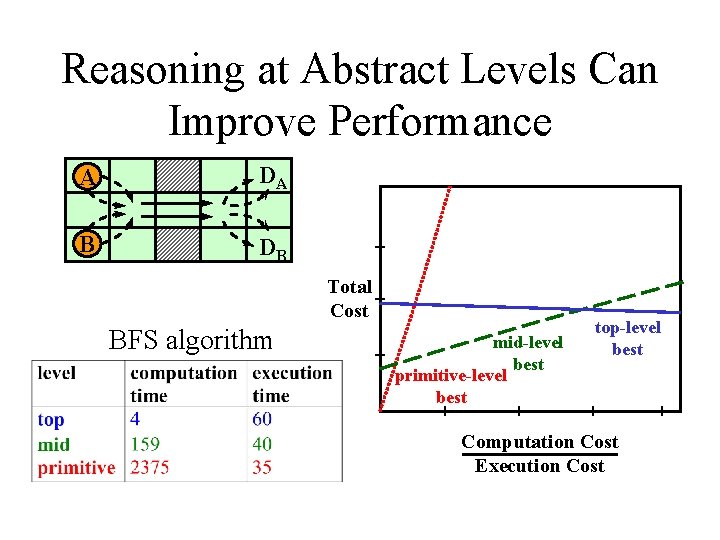
Reasoning at Abstract Levels Can Improve Performance A DA B DB Total Cost BFS algorithm mid-level best primitive-level best top-level best Computation Cost Execution Cost

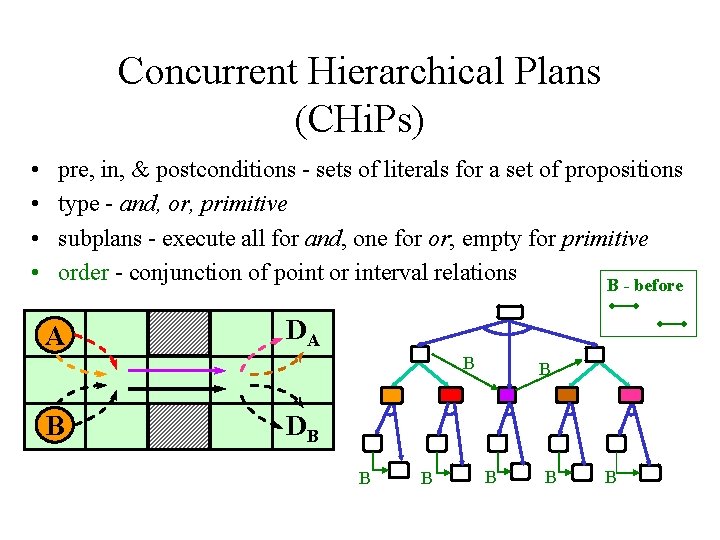
Concurrent Hierarchical Plans (CHi. Ps) • • pre, in, & postconditions - sets of literals for a set of propositions type - and, or, primitive subplans - execute all for and, one for or; empty for primitive order - conjunction of point or interval relations B - before A DA B B B DB B B

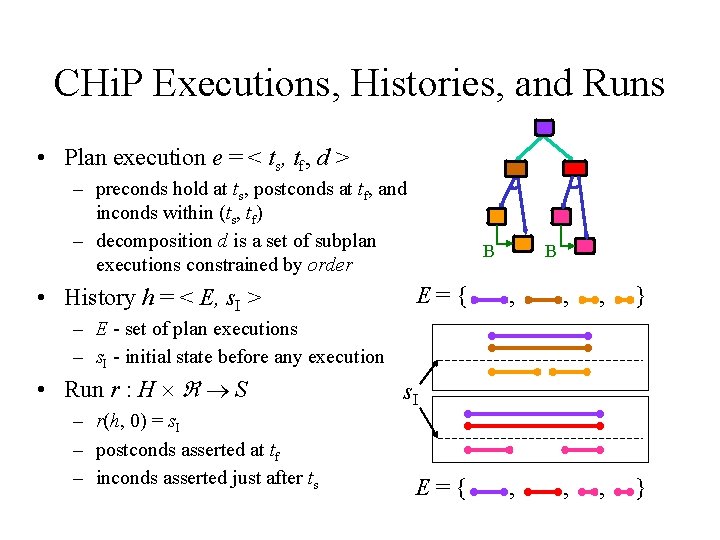
CHi. P Executions, Histories, and Runs • Plan execution e = < ts, tf, d > – preconds hold at ts, postconds at tf, and inconds within (ts, tf) – decomposition d is a set of subplan executions constrained by order • History h = < E, s. I > B E={ B , , , } – E - set of plan executions – s. I - initial state before any execution • Run r : H S – r(h, 0) = s. I – postconds asserted at tf – inconds asserted just after ts s. I E={

Asserting, Clobbering, Achieving, Undoing e • e asserts in/postcondition l at t l • e achieves precondition l of e' • e clobbers pre/in/postcondition l of e' e l e' l e e' l l e l l • e undoes postcondition l of e' l e' e' l e' l e l • must - for all executions in all histories • may - for some execution in some history l l

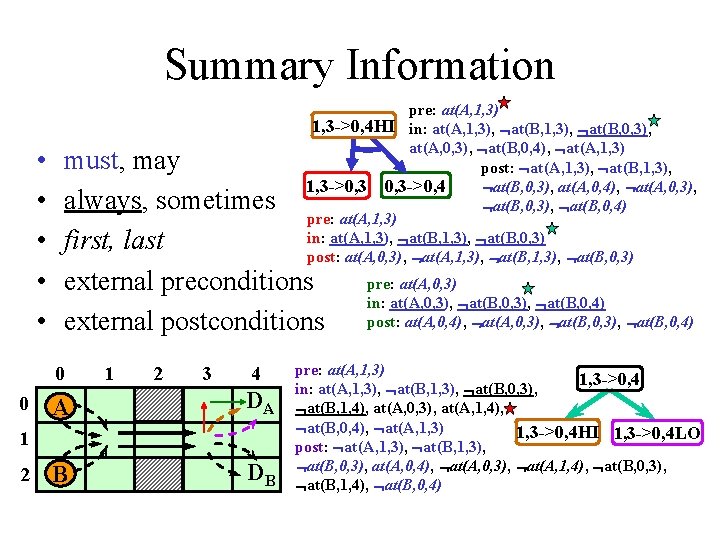
Summary Information • • • pre: at(A, 1, 3) 1, 3 ->0, 4 HI in: at(A, 1, 3), at(B, 0, 3), at(A, 0, 3), at(B, 0, 4), at(A, 1, 3) post: at(A, 1, 3), at(B, 0, 3), at(A, 0, 4), at(A, 0, 3), 1, 3 ->0, 3 ->0, 4 at(B, 0, 3), at(B, 0, 4) pre: at(A, 1, 3) in: at(A, 1, 3), at(B, 0, 3) post: at(A, 0, 3), at(A, 1, 3), at(B, 0, 3) must, may always, sometimes first, last external preconditions external postconditions 0 0 1 2 3 4 A DA B DB 1 2 pre: at(A, 0, 3) in: at(A, 0, 3), at(B, 0, 4) post: at(A, 0, 4), at(A, 0, 3), at(B, 0, 4) pre: at(A, 1, 3) 1, 3 ->0, 4 in: at(A, 1, 3), at(B, 0, 3), at(B, 1, 4), at(A, 0, 3), at(A, 1, 4), at(B, 0, 4), at(A, 1, 3) 1, 3 ->0, 4 HI 1, 3 ->0, 4 LO post: at(A, 1, 3), at(B, 0, 3), at(A, 0, 4), at(A, 0, 3), at(A, 1, 4), at(B, 0, 3), at(B, 1, 4), at(B, 0, 4)

Deriving Summary Information • Recursive procedure bottoming out at primitives • Derived from those of immediate subplans • O(n 2 c 2) for n plans in hierarchy and c conditions in each set of pre, in, and postconditions • Proven procedures for determining must/may achieve/undo/clobber • Properties of summary conditions are proven based on procedure

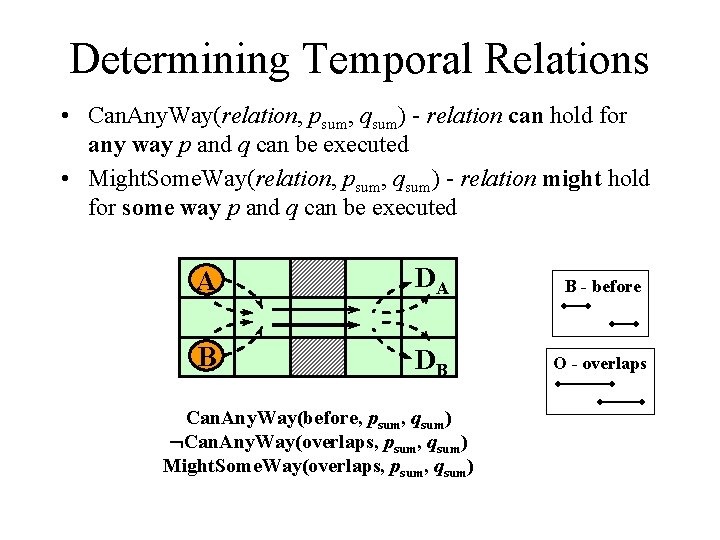
Determining Temporal Relations • Can. Any. Way(relation, psum, qsum) - relation can hold for any way p and q can be executed • Might. Some. Way(relation, psum, qsum) - relation might hold for some way p and q can be executed A DA B - before B DB O - overlaps Can. Any. Way(before, psum, qsum) Can. Any. Way(overlaps, psum, qsum) Might. Some. Way(overlaps, psum, qsum)

Determining Temporal Relations among Abstract Plans • Can. Any. Way(order, Psum) - all executions succeed for all plans with summary info Psum for all histories Might. Some. Way(order, Psum) - all executions succeed for some set of plans with summary info Psum for some history – Psum is a set of summary information for a group of plans – order is a conjunction of point/interval relation constraints • CAW and MSW are proven sound and complete – Proof takes advantage of must-clobber and may-clobber – Rules identify threats to resolve (resources in contention)

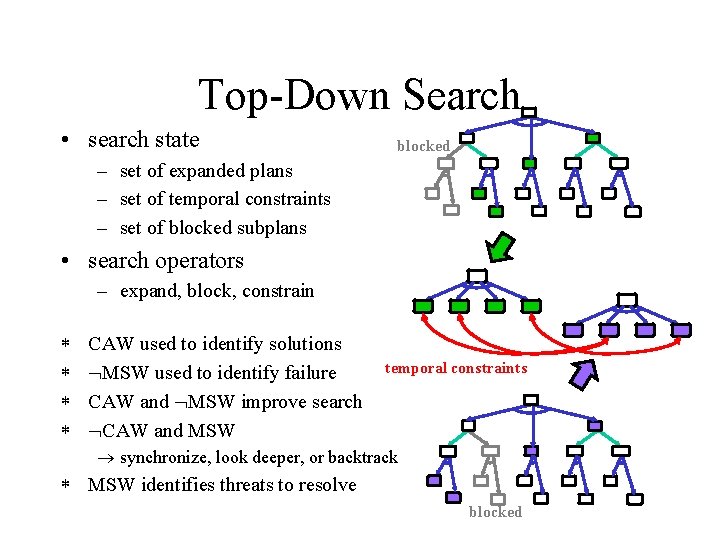
Top-Down Search • search state blocked – set of expanded plans – set of temporal constraints – set of blocked subplans • search operators – expand, block, constrain * * CAW used to identify solutions MSW used to identify failure CAW and MSW improve search CAW and MSW temporal constraints synchronize, look deeper, or backtrack * MSW identifies threats to resolve blocked

Summary of Contributions • General model of concurrent interaction of hierarchical plans • Formalization of planning concepts • Proven properties of summary information • Sound and complete rules for determining temporal relations • Toolbox for building sound and complete planning and coordination mechanisms

Work in Progress & Future Work • Constructing a concurrent hierarchical planner • Coordinating overlapping goals – Adopting other agents’ plans/goals • Dealing with global plan failure during execution • Summarizing plan information differently (probabilistic) • Handling more expressive plan representations • Scaling number of agents and difficulty of coordination • Interleaving planning, execution, and coordination

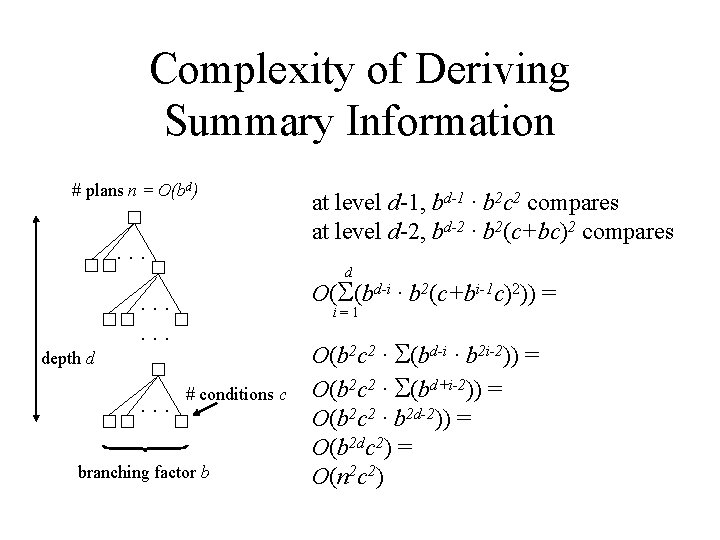
Complexity of Deriving Summary Information # plans n = O(bd) . . . at level d-1, bd-1 · b 2 c 2 compares at level d-2, bd-2 · b 2(c+bc)2 compares d O( (bd-i · b 2(c+bi-1 c)2)) = . . . i=1 depth d . . . # conditions c branching factor b O(b 2 c 2 · (bd-i · b 2 i-2)) = O(b 2 c 2 · (bd+i-2)) = O(b 2 c 2 · b 2 d-2)) = O(b 2 dc 2) = O(n 2 c 2)

Difficulty of CAW and MSW 0 1 Rule Specification • MSW(overlaps, psum, qsum) • false if postconditions conflict – unsound • false if conflicts with pin and qpre qin or ppost and qin where – pin is set of must, always inconds of p not achieved by inconds of q – ppost is set of postconds of p – qpre is set of must preconds of q not achieved by in- or postconds of p – qin is set of must, always inconds of p not achieved by inconds of p 0 O - overlaps A 1 2 B pre: at(A, 0, 0) in: at(A, 0, 0), at(A, 0, 1), at(A, 1, 1), at(B, 0, 0), at(B, 0, 1), at(B, 1, 0) post: at(A, 0, 0), at(A, 0, 1), at(A, 1, 1), at(A, 1, 0), at(B, 0, 1), at(B, 1, 0) pre: at(B, 2, 0) in: at(B, 2, 0), at(B, 2, 1), at(B, 1, 1), at(A, 2, 0), at(A, 2, 1), at(A, 1, 0) post: at(B, 2, 0), at(B, 2, 1), at(B, 1, 1), at(B, 1, 0), at(A, 2, 1), at(A, 1, 0)