Theories of Covalent Bonding Molecular Orbital Theory By

Theories of Covalent Bonding Molecular Orbital Theory By Prof. Dr. Adil Ali

MOLECULAR ORBITAL THEORY ¢ VSEPR and VB theory explain the shape of molecules but they were unable to explain the questions about magnetic and spectral properties, orbital energy levels and bond energy. ¢ MOT can explain all the answers about these questions.

Molecular Orbital Theory ¢ A model that describes a molecule as a collection of nuclei and electrons in which the electrons occupy orbitals that extend over the entire molecule.

Molecular orbital ( MO) ¢ An orbital of given energy and shape that extend over a molecule and can be occupied by no more than two electrons. Formation of molecular orbitals can be achieved by Combination of Atomic orbitals. Because of the complications arising from electron repulsions when we solve Schrodinger equation for many-electron atoms, thus the simplest and most common approximation was used to obtain the energies and shapes of the molecular orbitals called Linear Combination of Atomic Orbitals ( LCAO). LCAO assumed that MOs are derived from a linear combination of atomic orbitals.

The General Themes of MO Theory ¢ mathematically, LCAO means combines (add or subtract) the atomic orbitals ( atomic wave functions) of nearby atoms to form the molecular orbitals ( molecular wave functions). A molecule is viewed on a quantum mechanical level as a collection of nuclei surrounded by delocalized molecular orbitals. The number of molecular orbitals produced is always = # of atomic orbitals brought by the combining atoms (only orbitals on different atoms are combined).

If wave functions reinforce each other, a bonding MO is formed (region of high electron density exists between the nuclei). If wave functions cancel each other, an antibonding MO is formed (a node of zero electron density occurs between the nuclei). Atomic orbitals combine most effectively with orbitals of the similar energy and orientation

Number of MOs in a molecule equal to the sum of AOs of the two bonded atoms Number of electrons in MOs in a molecules equal to the sum of electrons in AOs of the two bonded atoms.

Bonding molecular orbital: A molecular orbital formed when wave functions are added to each other, which increases electron density between the nuclei. Electron occupying such an orbital stabilize the molecule. Antibonding molecular orbital: A molecular orbital formed when wave functions are subtracted to each other, which has a node between the nuclei. Node is a region of an orbital in which the electron density between the nuclei is zero Nonbonding molecular orbital A molecular orbital that is not involved in bonding

Filling molecular orbitals with electrons q. The same principle that they follow in filling AOs. Ø Orbitals are filled in order of increasing energy ( aufbau principle) Ø An orbitals has maximum capacity of two electrons with opposite spins ( Pauli exclusion principle) Ø Orbitals of equal energy are half filled, with spins parallel, before any is filled (Hund’s rule)

H 2 molecule When two H nuclei lie near each other, their atomic orbitals overlap Adding their wave functions together forms a bonding molecular orbital, which has a region of high electron density between the nuclei This additive overlap is analogous to the overlap of two light waves that reinforce each other and make the resulting wave brighter. For overlap increases the probability of the electron being between the nuclei An analogy between light waves and atomic wave functions. Amplitudes of wave functions added

The bonding MO (δ 1 s ) forms from addition of the Aos and is lower in energy than AOs. The bonding MO in H 2 is spred mostly between the nuclei atracted to the intervening electrons. An electron in this MO can delocalize its charge over a much larger volume than is possible in its separate AOs. because of this electrostatic attraction and charge delocalization, (electron density) lies between the nuclei, the energy of the bonding MO is lower than that of the isolated AOs. Therefore, when electrons occupy this orbita, the molecule is more stable than the separate atoms.

Subtracting the atomic functions from each other, forms an antibonding molecular orbital, which has a node between the nuclei This subtractive is analogous to the disappear of two light waves when two light waves cancel each other When overlap decreases, the probability of the electron being between the nuclei will decrease to reach zero (node) An analogy between light waves and atomic wave functions. Amplitudes of wave functions subtracted.

the antibonding orbital has a node between the nuclei and most of its electron density outside the internuclear region. Antibonding MO locationincreases nuclear repulsion and makes its energy higher than the isolated AOs. Therefore, when the antibonding orbital is occupied, the molecular is less stable than when the orbital is empty.

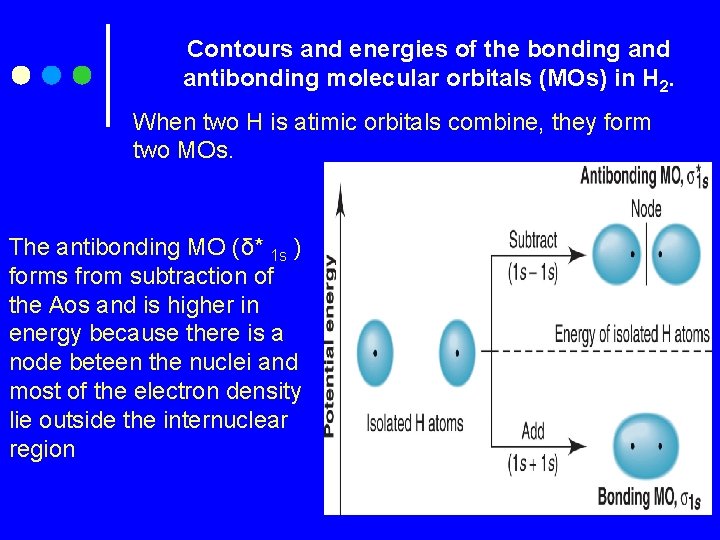
Contours and energies of the bonding and antibonding molecular orbitals (MOs) in H 2. When two H is atimic orbitals combine, they form two MOs. The antibonding MO (δ* 1 s ) forms from subtraction of the Aos and is higher in energy because there is a node beteen the nuclei and most of the electron density lie outside the internuclear region

MOLECULAR ORBITAL THEORY BOND ORDER in Lewis structure: the number of bonding e- pairs shared by 2 atoms in a molecule The MO Bond order: Is the number of electrons in bonding MOs minus the number of electrons in antibonding MOs, divided by two. B. O. = ½(# of e- in bonding orbitals – # of e- in antibonding orbitals) Fractional bond orders are possible in MO Theory!

Molecular Orbital Diagram MOD ¢ a diagram show the relative energy and the number of electrons in each MO, as well as the AOs that originally held the electrons. MOD in the s-block diatomic molecules Such as H 2, He 2, Li 2, Be 2, etc

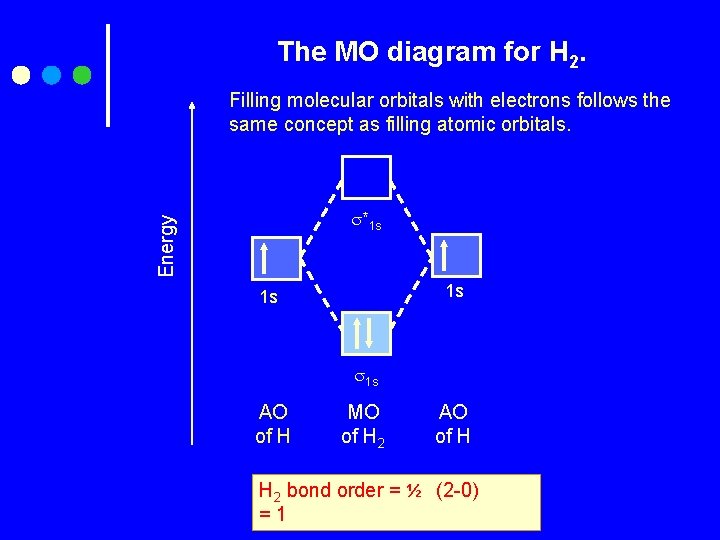
The MO diagram for H 2. Filling molecular orbitals with electrons follows the same concept as filling atomic orbitals. Energy *1 s 1 s 1 s AO of H MO of H 2 AO of H H 2 bond order = ½ (2 -0) =1

Two AOs (1 s 1 and 1 s 1) combine together by linear combination of atomic orbital to form two MOs (δ 1 s and δ*1 s ) Two electrons ( one from each H atom) are distribution in MOs in order to the relative energies. So, two electrons in bonding MO δ 1 s and zero electrons in antibonding MO δ*1 s Bond order= ½ (No. of es in bonding MOs) - (No. of es in antibonding MOs) = ½ (2 -0) =1 We predict that molecule does exist The magnetic behavior : diamagnetic The complete electronic configuration of H 2 : The valence electron configuration of H 2 : ( δ 1 s)2

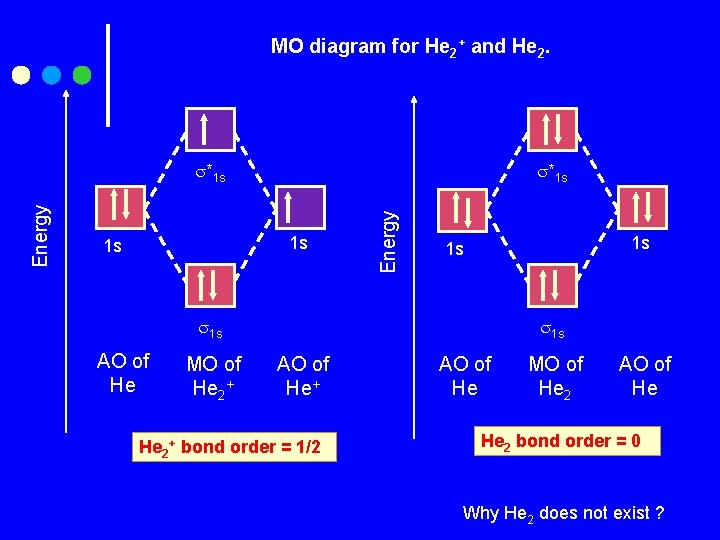
MO diagram for He 2+ and He 2. *1 s 1 s 1 s Energy *1 s 1 s 1 s AO of He MO of He 2+ 1 s AO of He+ He 2+ bond order = 1/2 AO of He MO of He 2 AO of He He 2 bond order = 0 Why He 2 does not exist ?

Two AOs (1 s 2 and 1 s 2) of two He atoms combine together by linear combination of atomic orbital to form two MOs (δ 1 s and δ*1 s ) four electrons ( two from each H atom) are distribution in MOs in order to the relative energies. So, two electrons in bonding MO δ 1 s and two electrons in antibonding MO δ*1 s Bond order= ½ (No. of es in bonding MOs) - (No. of es in antibonding MOs) = ½ (2 -2) =0 We predict that molecule does not exist The magnetic behavior : diamagnetic The complete electronic configuration of He 2 : ( δ 1 s)2 (δ*1 s)2 The valence electronic configuration of He 2 : (δ*1 s)2

Why He 2 does not exist ? He 2 has four electrons to place its δ 1 s and δ*1 s MOs. Both the bonding and antibonding orbitals are filled. The stabilization gained by electron pair in the bonding MO is canceled by the destabilization from the electron pair in the antibonding MO. From its zero bond order ½ (2 -2)= 0, we predict that He 2 does not exist.

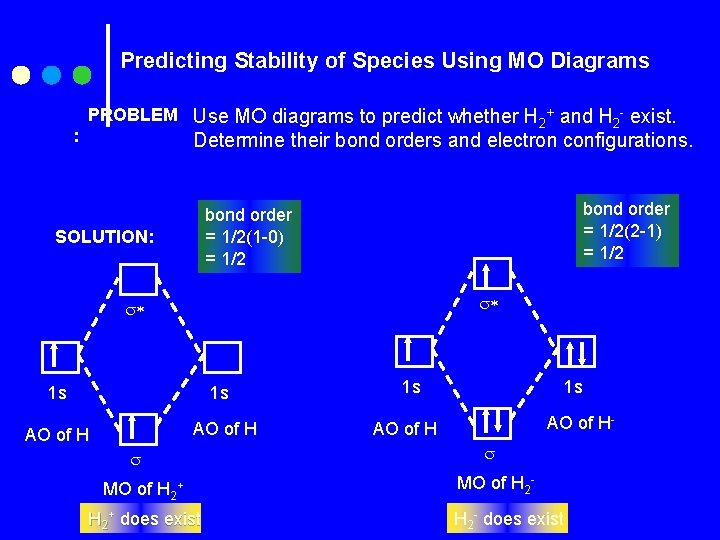
Predicting Stability of Species Using MO Diagrams : PROBLEM Use MO diagrams to predict whether H 2+ and H 2 - exist. Determine their bond orders and electron configurations. bond order = 1/2(2 -1) = 1/2 bond order = 1/2(1 -0) = 1/2 SOLUTION: 1 s 1 s AO of H MO of H 2+ does exist 1 s 1 s AO of H- AO of H MO of H 2 - does exist

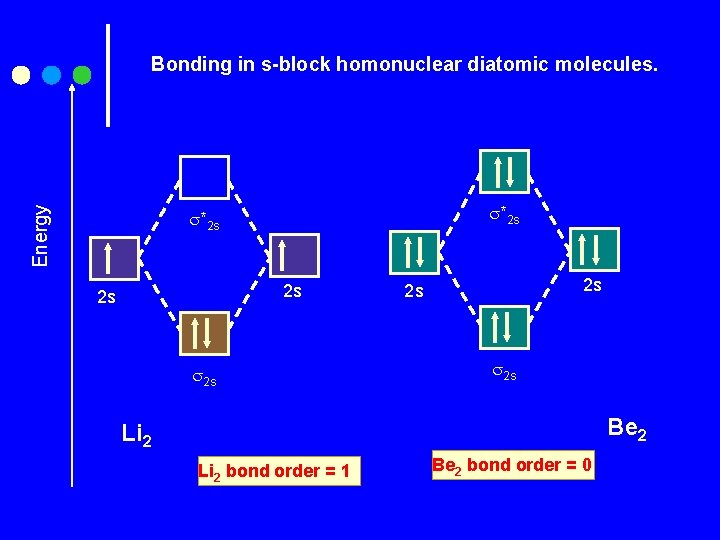
Energy Bonding in s-block homonuclear diatomic molecules. *2 s 2 s 2 s 2 s Be 2 Li 2 bond order = 1 Be 2 bond order = 0

Molecular Orbitals from atomic p-orbital combination p – orbitals can interact with each other from two different directions. 1 - End- to- End combination gives a pair of δ MOs (δ 2 p and δ* 2 p) which the greatest electron density located between the nuclei. 2 - side - to – side combination gives a pair of π MOs ( π2 p and π*2 p ) have a node between the nuclei and most of their electron density outside the interaction region of nuclei. So, Pi (π) molecular orbital: A molecular orbital formed by combination of two atomic ( usually p) orbitals whose orientation are perpendicular to the internuclear axis.

The order of MO energy levels 1 - MOs formed from 2 p orbitals are higher in energy than MOs that formed from 2 s orbitals because 2 p AOs are higher in energy than 2 s AOs. 2 - monding MOs are lower in energy than antibonding MOs , so (δ 2 p is lower than δ*2 p) ; and π2 p is lower than and π*2 p. 3 - End to End overlap is greater than side to side overlap, so δ 2 p Mois lower in energy than π2 p. The destabilizing effect of the δ*2 p MO is greater than that of the π*2 p Thus, the energy order for MOs derived from 2 p orbitals is δ 2 p <π2 p< π*2 p< δ*2 p

the energy order for MOs derived from 2 p orbitals δ 2 p <π2 p< π*2 p< δ*2 p is true when p orbtals more than half-filled (p 4, p 5 and p 6) Is based on the assumption that the s and p AOs are so different in energy that result from the electron repulsion that occur between the 2 p electron pairs which lead to up raise the energy of the 2 p orbitals compared to energy of 2 s orbital, therefore , they do not interact with each other. So, the orbitals do not mix. When 2 p AOs are being half filled (P 3) or less than half –filled (p 1, p 2) , the energies of p AOs are closer to the energy of 2 s orbital , because the repulsions are very small between electron of p orbital therefore , therefore, they do interact with each other. As a result, some mixing occurs between the 2 s orbital of one atom and the end one of 2 p orbital of the other. π2 p < δ 2 p < π*2 p< δ*2 p

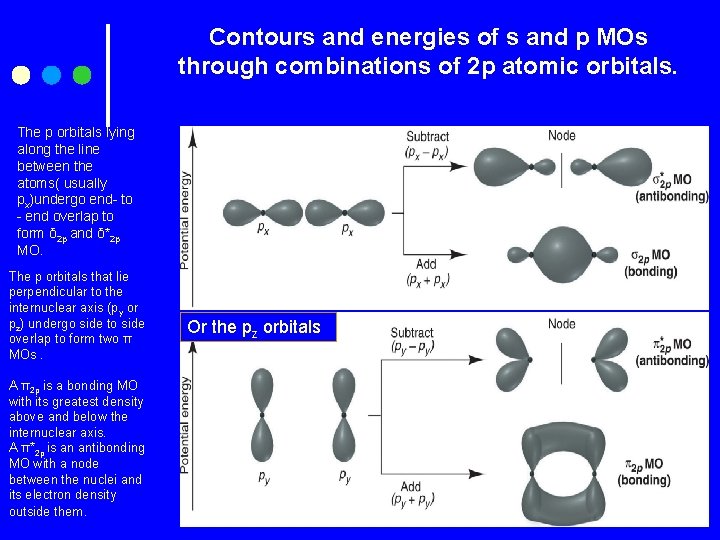
Contours and energies of s and p MOs through combinations of 2 p atomic orbitals. The p orbitals lying along the line between the atoms( usually px)undergo end- to - end overlap to form δ 2 p and δ*2 p MO. The p orbitals that lie perpendicular to the internuclear axis (py or pz) undergo side to side overlap to form two π MOs. A π2 p is a bonding MO with its greatest density above and below the internuclear axis. A π*2 p is an antibonding MO with a node between the nuclei and its electron density outside them. Or the pz orbitals

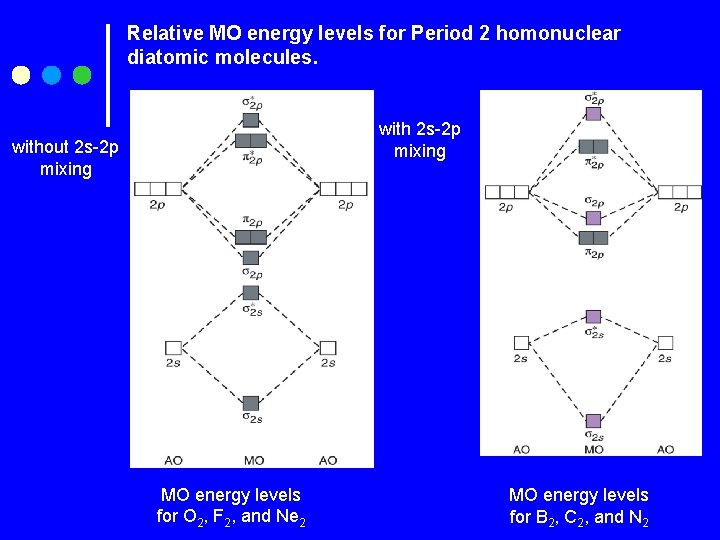
Relative MO energy levels for Period 2 homonuclear diatomic molecules. with 2 s-2 p mixing without 2 s-2 p mixing MO energy levels for O 2, F 2, and Ne 2 MO energy levels for B 2, C 2, and N 2

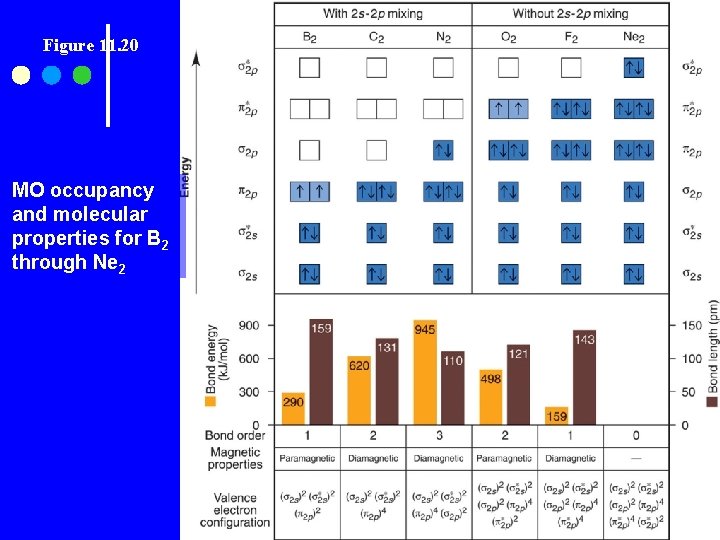
Figure 11. 20 MO occupancy and molecular properties for B 2 through Ne 2

Using MO Theory to Explain Bond Properties PROBLEM: As the following data show, removing an electron from N 2 forms an ion with a weaker, longer bond than in the parent molecules, whereas the ion formed from O 2 has a stronger, shorter bond: N 2 + O 2 + Bond energy (k. J/mol) 945 841 498 623 Bond length (pm) 110 112 121 112 Explain these facts with diagrams that show the sequence and occupancy of MOs. SOLUTION: N 2 has 10 valence electrons, so N 2+ has 9. O 2 has 12 valence electrons, so O 2+ has 11.

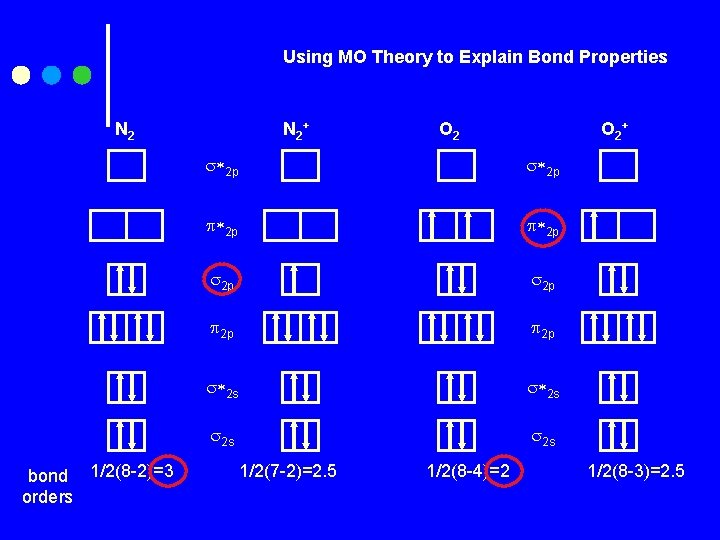
Using MO Theory to Explain Bond Properties N 2 bond 1/2(8 -2)=3 orders N 2 + O 2 + 2 p 2 p 2 s 2 s 1/2(7 -2)=2. 5 1/2(8 -4)=2 1/2(8 -3)=2. 5

MO Theory Practice 1. Draw the bonding and antibonding molecular orbitals for H 2. 2. Do Valence Bond Theory (hybridization) and MO Theory for both O 2 and O 22 -. Which theory works better to explain the molecule and ion? 3. For N 2, N 2+ and N 2 - compare a. Magnetic character b. Net number of bonds c. Bond Order d. Bond length e. Bond strength

Answers 1. See picture in text. 2. VB Theory shows O 2 as sp 2 hybridized with one bond and one bond. There are two lone pairs on each O. O 22 - has one bond, and each O has three lone pairs. MO Theory shows a bond order of 2 for O 2 and that it is paramagnetic. MO Theory shows a bond order of 1 for O 22 - and diamagnetic. But MO Theory fits the real data that O 2 is paramagnetic.

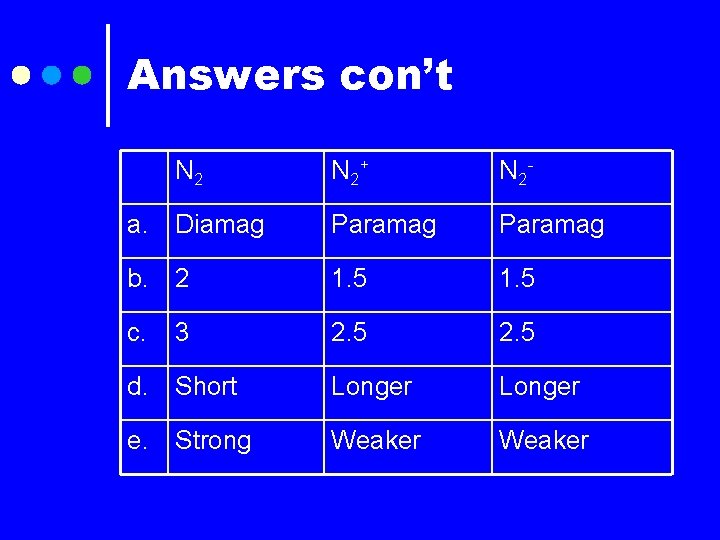
Answers con’t N 2+ N 2 - a. Diamag Paramag b. 2 1. 5 c. 3 2. 5 d. Short Longer e. Strong Weaker

MOD of Some Heteronuclear Diatomic Molecules Heteronuclear diatomic molecules: Molecules which have two different atoms In polar covalent molecule MOD is asymmetric ? ? ? Because the atomic orbitals of the two atoms have unequal energies. Generally, atoms with greater effective nuclear charge (Zeff) i. e, small size and high electronegative atom has lower energy AOs , therefore they draw their electrons closer to the nucleus.

Let us apply MOT to the bonding in HF and NO v In HF molecule, because of F atom is more electronegative atom than H atom, so, F orbitals to be of lower energy than 1 s orbital of H, so 2 p electrons of F are closer to the nucleus. 1 s orbital of H combine only with the 2 px orbital of F atom which lead to End – to – End overlap and results an δ and δ* MOs. The two other p orbitals of F (2 py and 2 pz) are not involved in bonding which called nonbonding MOs and have the same energies as AOs.

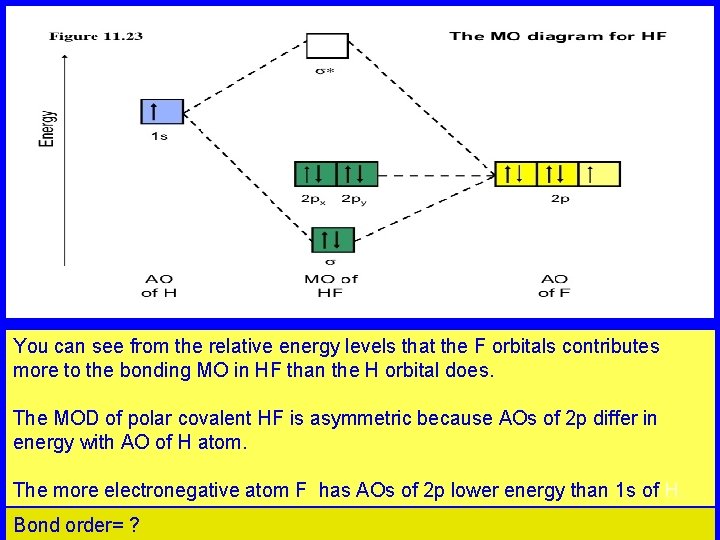
You can see from the relative energy levels that the F orbitals contributes more to the bonding MO in HF than the H orbital does. The MOD of polar covalent HF is asymmetric because AOs of 2 p differ in energy with AO of H atom. The more electronegative atom F has AOs of 2 p lower energy than 1 s of H. Bond order= ?

NO molecule NO is a highly reactive molecule due to its lone electron. Two possible Lewis structures for NO, with formal charges: Both structures show a double bond, but the measured bond energy suggested a bond order higher than 2. 0 0 MOT predict the bond order and indicates lone electron placement with no difficulty. The MOD is skewed because the AOs of the more electronegative O are lower in energy than AOs of N, -1 +1

v In NO molecule, because of O atom is more electronegative atom than N atom, so, 2 s and 2 p of O orbitals to be of lower energy than 2 s and 2 p orbital of N, (i. e. 2 s and 2 p electrons of O are closer to the nucleus). 2 s orbital of O combine with the 2 s orbital of N atom which lead to End – to – End overlap and results an δ 2 s and δ* 2 s MOs. 2 p orbitals of O combine with the 2 p orbital of N atom as following 2 px AO of O combine with 2 px AO which lead to End – to – End overlap and results an δ 2 s and δ*2 s MOs. 2 py and 2 pz AOs of O atom combine side – to- side with 2 py and 2 pz AOs respectively to form π2 p an π*2 p. 11 valence electrons enter MOs in order of increasing energy, leaving the lone electron in one of the π*2 p orbitals.

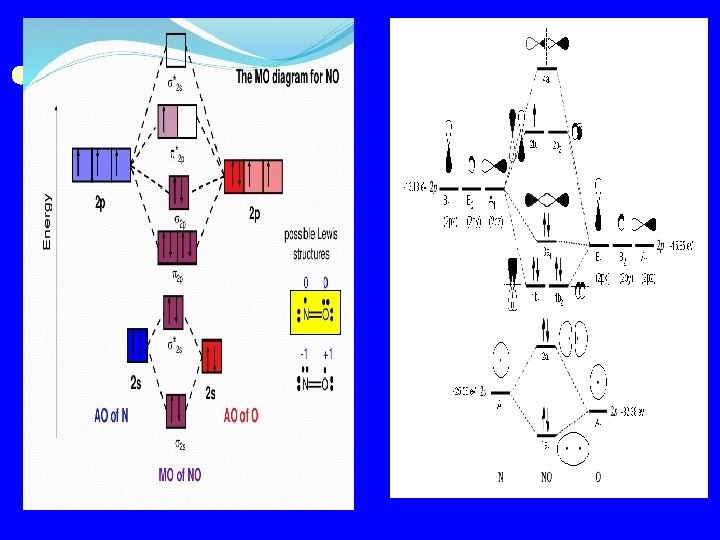
Bond order = ½ ( 8 -3) = 2. 5 The bonding electrons lie in MOs closer in energy to the AOs of the O atom. The lone electron occupies an antibonding orbital. Because this orbital receives a greater energy contribution from the 2 p orbital of N, the lone electron resides closer to the N atom.