Theoretical understanding of the problem with a singular

Theoretical understanding of the problem with a singular drift term in the complex Langevin method Jun Nishimura (KEK Theory Center, SOKENDAI) May 13, 2015, QCD club at University of Tokyo, Hongo Ref. ) J. N. -Shimasaki: 1504. 08359 [hep-lat] Nagata-J. N. -Shimasaki : in preparation

Complex action problem Path integral Monte Carlo simulation Generate ensemble of Calculate VEV with the probability by taking an ensemble average of a power tool to study QFT in a fully nonperturbative manner However, in many interesting examples, the action S becomes complex! l QCD at finite density or with theta term l supersymmetric gauge theories and matrix models relevant to superstring theory can no longer be regarded as the Boltzmann weight !

complex Langevin equation Stochastic quantization for real S Parisi-Wu (’ 81) fictitious time evolution of Langevin equation drift term Gaussian white noise VEV can be obtained by time averaging over after thermalization Use the same method for complex S A real scalar field Parisi (’ 83), Klauder(’ 83) , then, becomes a complex scalar field. complex Langevin equation

Recent development in finite density QCD based on complex Langevin eq. Using various techniques, CLE turned out to work successfully in: l Finite density QCD in the deconfined phase with relatively heavy quarks Sexty: PLB 729 (2014) 108 = ar. Xiv: 1307. 7748 [hep-lat] See also reviews Sexty: 1410. 8813 [hep-lat] Arts et al. : 1412. 0847 [hep-lat] l Random Matrix Theory for finite density QCD (T=0) with arbitrary quark mass (including the massless limit!) Mollgaard, Splittorff: 1412. 2729 [hep-lat] related paper: Splittorff: 1412. 0502 [hep-lat]

Problems with log singularies in the action (previous arguments) e. g. , Mollgaard, Splittorff: 1309. 4335 [hep-lat] Using the drift term : corresponds to considering with a branch cut as a multi-valued function When the phase of rotates frequently, complex Langevin method gives wrong results. “branch cut crossing problem” (Greensite: 1406. 4558 [hep-lat]) The issue of “non-holomorphicity of the action” (Sexty: 1410. 8813 [hep-lat])

Our new theoretical understanding • Formulation of the method only requires: ü Single-valuedness of the complex weight There is NO need to define the action through ü Single-valuedness of the drift term after complexification • The problem actually occurs due to the singularity in the drift term !

Plan of the talk 1. The basic idea of complex Langevin method stochastic quantization complex Langevin equation (CLE) the criterion for giving correct results 2. Theoretical understanding of the problem with log singularities Studies of the Fokker-Planck equation (FPE) The breakdown of the correspondence between FPE and CLE 3. Correct convergence even with severe sign problem 4. Non-logarithmic case 5. Two-variable case 6. “Gauge cooling” in random matrix theory 7. Summary and future prospects J. N. -Shimasaki: 1504. 08359 [hep-lat] Nagata-J. N. -Shimasaki : in preparation

1. THE BASIC IDEA OF COMPLEX LANGEVIN METHOD

Stochastic quantization Parisi-Wu (’ 81) For review, see Damgaard-Huffel (’ 87) View this as the stationary distribution of a stochastic process. Langevin eq. Gaussian white noise

Proof satisfies: Fokker-Planck eq. Define : “Fokker-Planck Hamiltonian” self-adjoint operator with non-negative spectrum unique eigenfunction with zero eigenvalue vanish at large t

Thus, we have shown: Note: ergodicity VEV of observables can be obtained by taking an average over a long time of the Langevin process !

Extension to a complex-action system Parisi (’ 83), Klauder (’ 83) Langevin eq. assumed to be real here The solution becomes complex, so we denote it as: The crucial question is: ?

Formal argument ? Ambjorn-Yang (’ 85) Suppose exists. Then, one can obtain: Moreover, one can show Fokker-Planck eq. , but with S complex ! is a stationary solution. If all the eigenvalues of this operator have negative real part, the convergence is guaranteed.

The most nontrivial assumption in the above argument is that should exist. This may be a too strong requirement. We may have to be satisfied with for a specific class of operators.

A refined argument Aarts, James, Seiler, Stamatescu: Eur. Phys. J. C(’ 11) 71; 1756 ? holds at t=0 if real positive Does it hold for t>0 when Evolution of evolves according to is derived from CLE as

Integration by parts requires, in particular: vanishes at large t Hence, we need sufficiently sharp fall off of P(x, y; t) in y-direction

2. THEORETICAL UNDERSTANDING OF THE PROBLEM WITH LOG SINGULARITIES

A simple example Define the drift term: single-valued for any p The action is multi-valued, but we DON’T need to use it !

Complex Langevin equation drift term real Gaussian noise satisfies Fokker-Planck like equation :

The crucial relation to the complex weight Fokker-Planck equation (FPE)

Solutions to the FPE time-independent solution : Necessary and sufficient conditions for the correct convergence of CLM : i) The relation ii) The solution holds. of the FPE asymptotes to w(x) at large t.
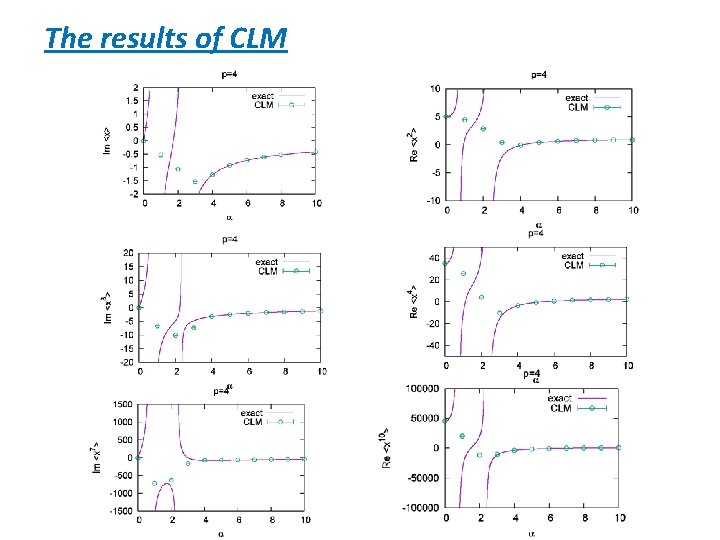
The results of CLM
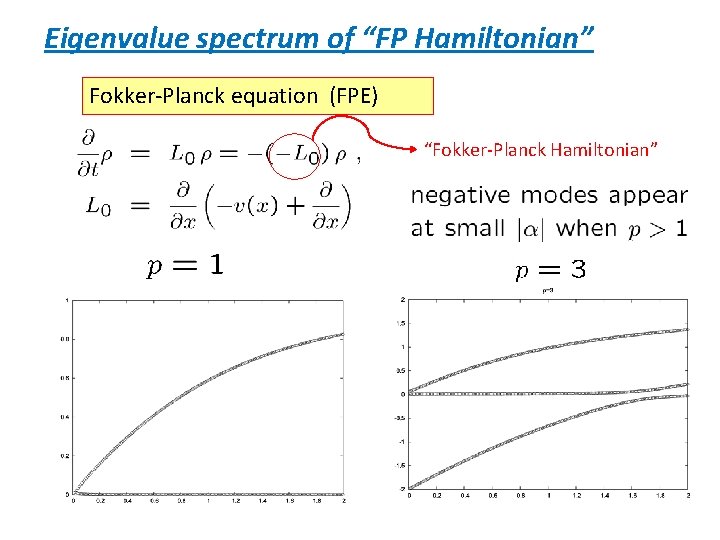
Eigenvalue spectrum of “FP Hamiltonian” Fokker-Planck equation (FPE) “Fokker-Planck Hamiltonian”

The eigenfunctions at . An extra zero mode when p is a positive odd integer.

An implication of the negative modes The most negative mode of the FP Hamiltonian Fokker-Planck equation (FPE) This behavior is incompatible with the relation : This relation must be violated, at least, in the region where the negative modes appear !

Relation between and P In order to derive this relation, one uses : (#) with the initial condition :

Proving eq. (#) Define an interpolating function LHS of (#) RHS of (#) Naively, this vanishes through integrating by parts. interpolated by the parameter

When does the partial integration fail ? l slow fall off of the integrand at Aarts-James-Seiler-Stamatescu, ar. Xiv: 1101. 3270 [hep-lat] c. f. ) This lead to the idea of gauge-cooling. Seiler-Sexty-Stamatescu, ar. Xiv: 1211. 3709 [hep-lat] This is not a problem in the present case. l the presence of singularities in the integrand J. N. -Shimasaki, ar. Xiv: 1504. 08359 [hep-lat]

In the present example The boundary terms :
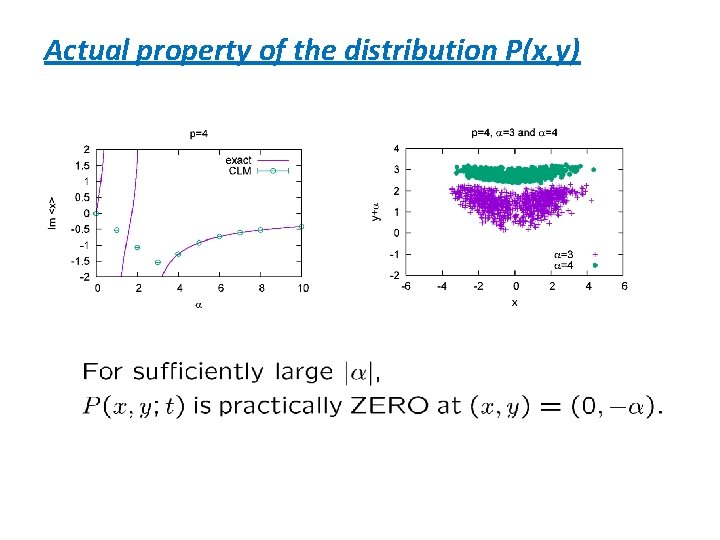
Actual property of the distribution P(x, y)

3. CORRECT CONVERGENCE EVEN WITH SEVERE SIGN PROBLEM

Relation to the phase rotation ? This causes the complex-action problem. NO, not necessarily ! In order to demonstrate this point, we study large p case.
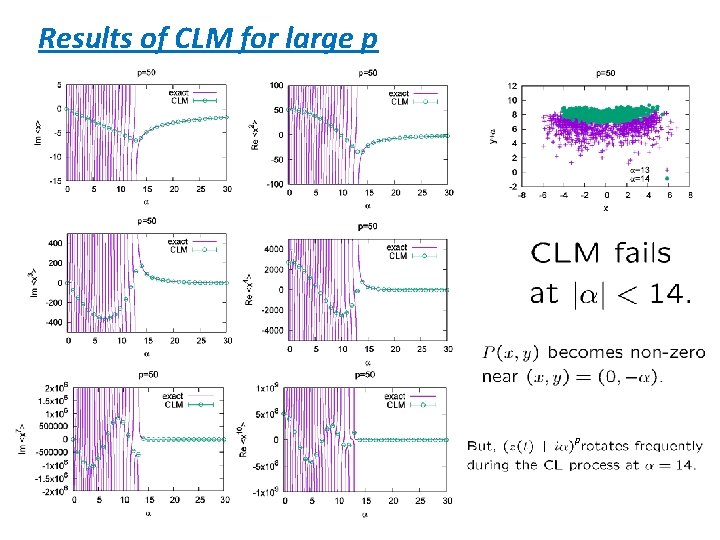
Results of CLM for large p p
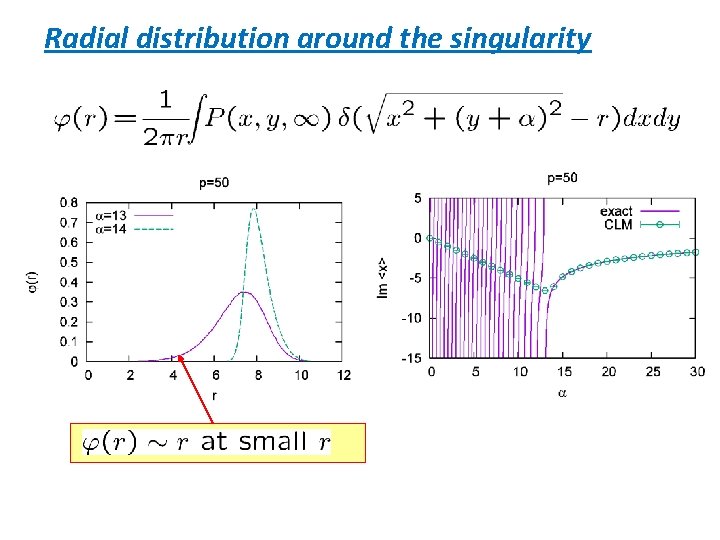
Radial distribution around the singularity

Severeness of the complex-action problem phase quenched model Reweighting method is extremely hard !

4. NON-LOGARITHMIC CASE

Non-logarithmic case single-valuedness of the drift term No issue of ambiguity associated with the branch cut !
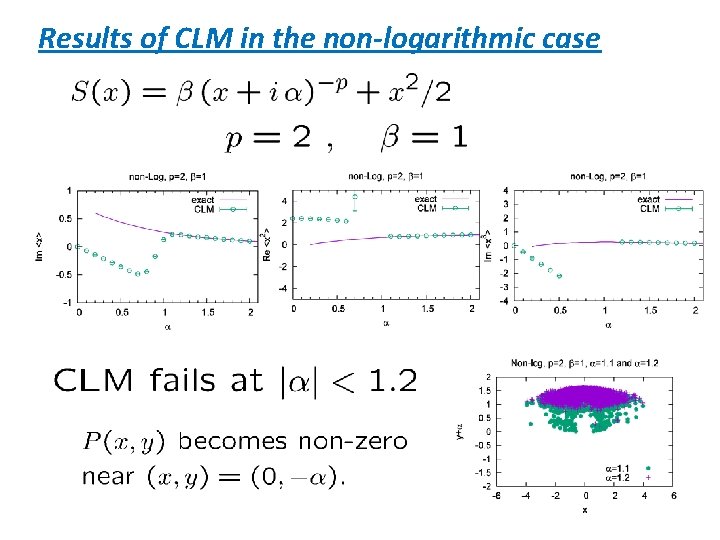
Results of CLM in the non-logarithmic case
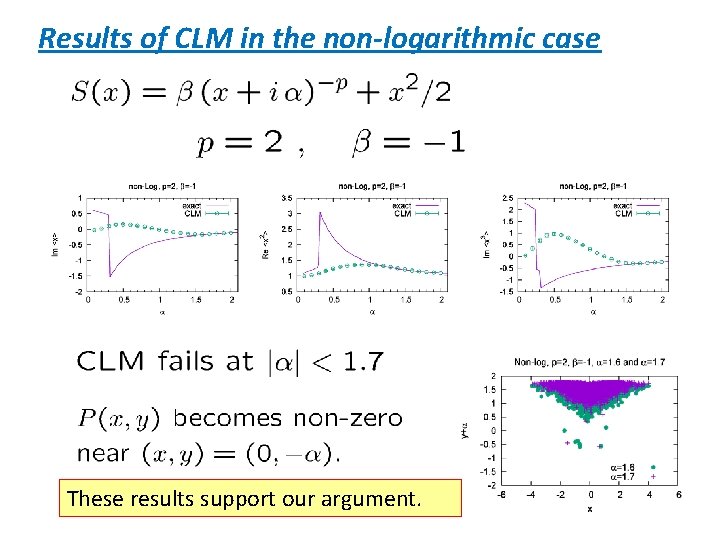
Results of CLM in the non-logarithmic case These results support our argument.

5. TWO-VARIABLE CASE
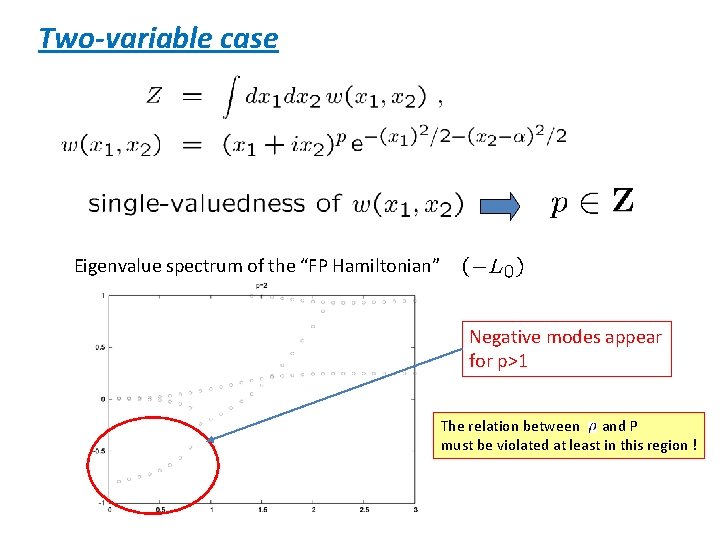
Two-variable case Eigenvalue spectrum of the “FP Hamiltonian” Negative modes appear for p>1 The relation between and P must be violated at least in this region !
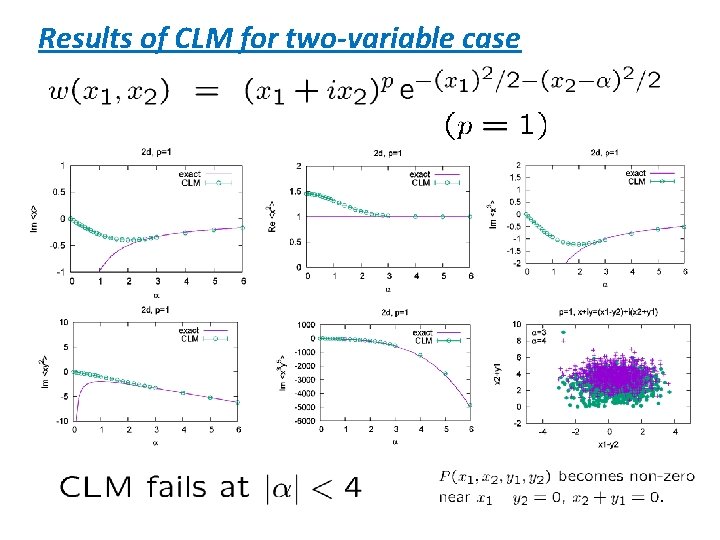
Results of CLM for two-variable case
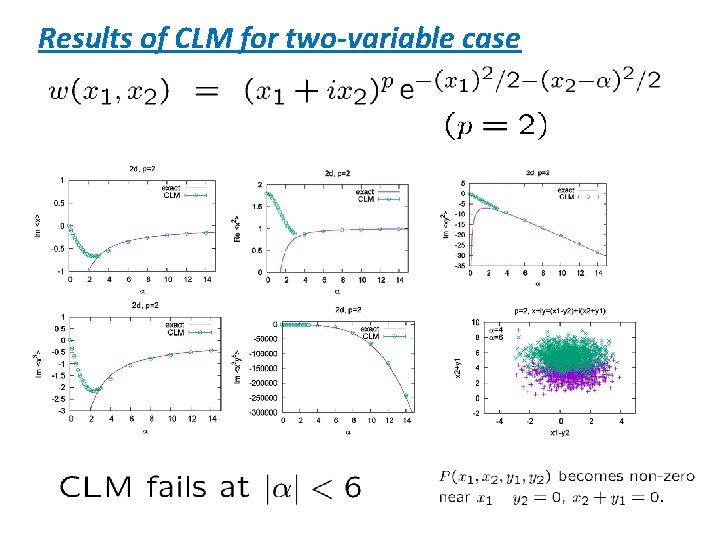
Results of CLM for two-variable case

6. GAUGE-COOLING IN RANDOM MATRIX THEORY

Application of CLM to finite density QCD For a review, see: Aarts 1302. 3028 [hep-lat] This term may cause the problem of the singular drift we have been discussing ! complex action problem

Complex Langegin eq. (discretized ver. ) The action should be written in terms of holomorphic variables. gauge symmetry:

“gauge cooling” Seiler, Sexty, Stamatescu: PLB 723 (’ 13) 213 Unitarity norm : d=0 only for SU(3) matrices. After each Langevin step, apply the gauge tr. in the direction of the steepest descent of the unitarity norm. full QCD simulations with staggered fermion Sexty: PLB 729 (’ 14) 108 Excursion in the imaginary directions is avoided.
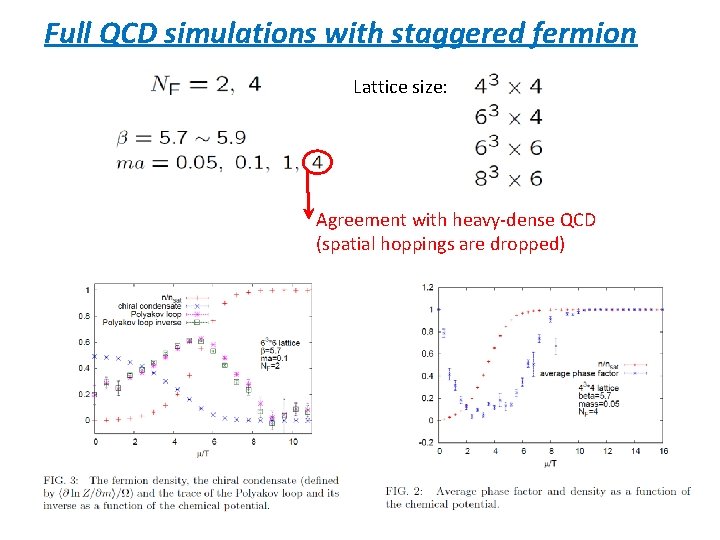
Full QCD simulations with staggered fermion Lattice size: Agreement with heavy-dense QCD (spatial hoppings are dropped)
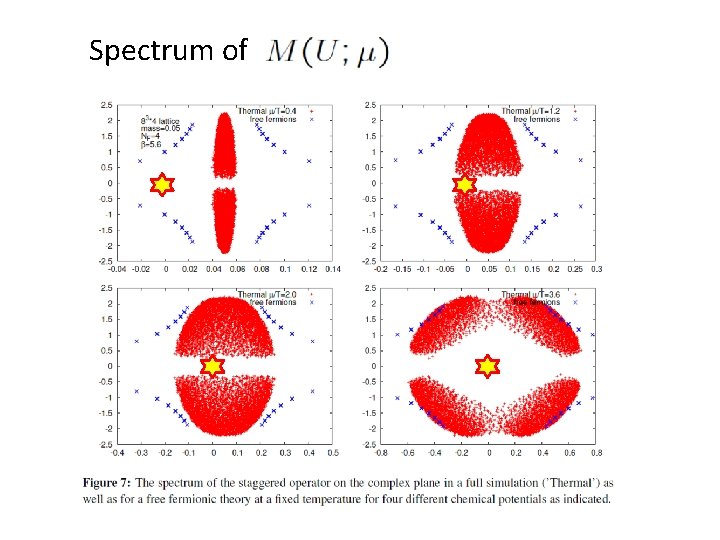
Spectrum of

Random Matrix Theory for finite density QCD The partition function is dominated by pions, which have zero quark charge.

CLM for Random Matrix Theory Complexification of dynamical variables :
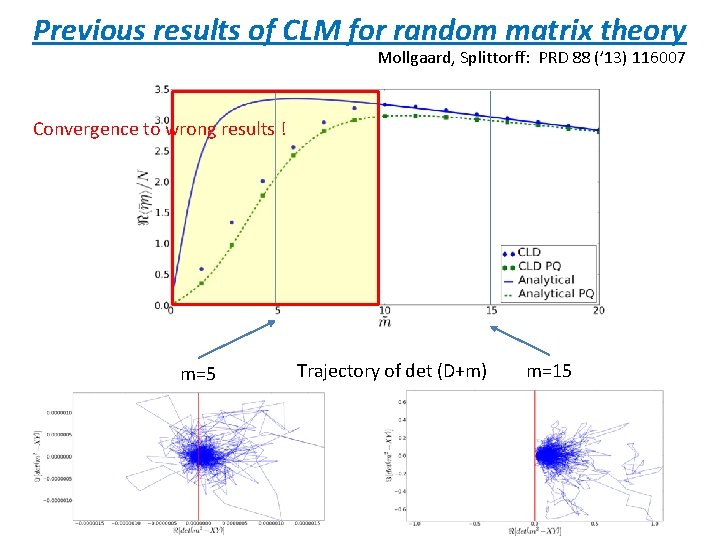
Previous results of CLM for random matrix theory Mollgaard, Splittorff: PRD 88 (’ 13) 116007 Convergence to wrong results ! m=5 Trajectory of det (D+m) m=15

“gauge-cooling” in random matrix theory Nagata-J. N. -Shimasaki, in prep. Symmetry of the system : complexfication of variables Using this complexified symmetry, we apply “gauge-cooling” after each Langevin step so that “anti-Hermiticity norm”
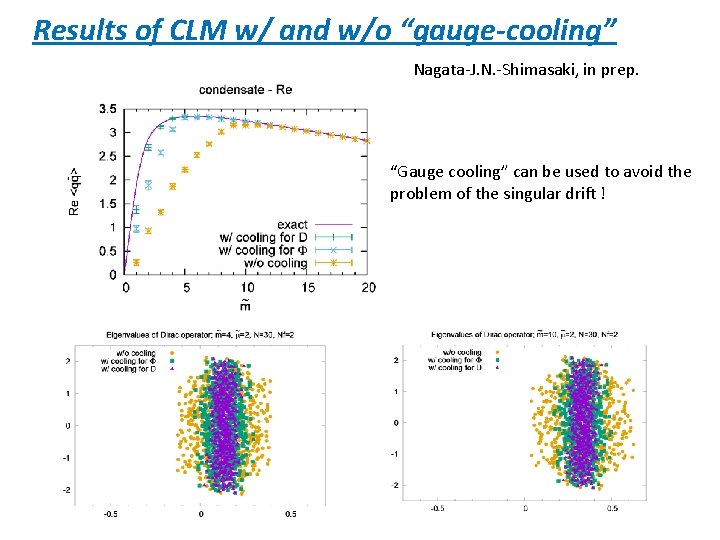
Results of CLM w/ and w/o “gauge-cooling” Nagata-J. N. -Shimasaki, in prep. “Gauge cooling” can be used to avoid the problem of the singular drift !

7. SUMMARY AND FUTURE PROSPECTS

Summary l Complex Langevin eq. a promising approach to a system with complex S Crucial questions are: (1) (2) convergence to (3) Violation of holomorphicity due to Ø We have clarified (3), which was poorly understood before. The convergence to wrong results is due to violation of (1).

Future prospects l Full QCD at finite density in the deconfined phase with relatively heavy quarks : successful “Gauge cooling” is the crucial technique. l Randam Matrix Theory serves as a testing ground for low T regime with light quarks. We have generalized the idea of “gauge cooling”. l Full QCD simulations in that region may be possible in the near future with “Gauge cooling” + some coordinate transformation + nontrivial kernels for the random noise l Applications to other complex-action systems such as supersymmetric gauge theories and matrix models relevant to nonperturbative studies of superstring theory
- Slides: 57