Theoretical Plate Model of Separation Origin of plate

Theoretical Plate Model of Separation

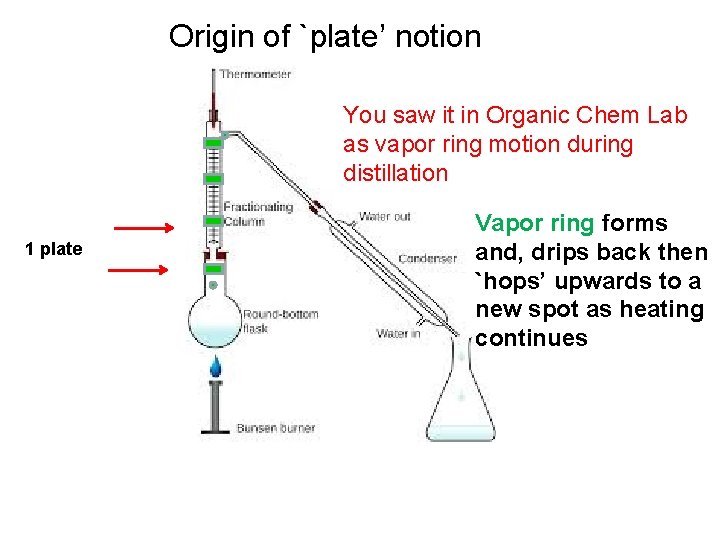
Origin of `plate’ notion You saw it in Organic Chem Lab as vapor ring motion during distillation 1 plate Vapor ring forms and, drips back then `hops’ upwards to a new spot as heating continues

Plates in the World of Petrochemicals 1 separation plate Pulloffs (distillate exits here) 220 Foot fractionating column Near Beaumont Tx Inside the column

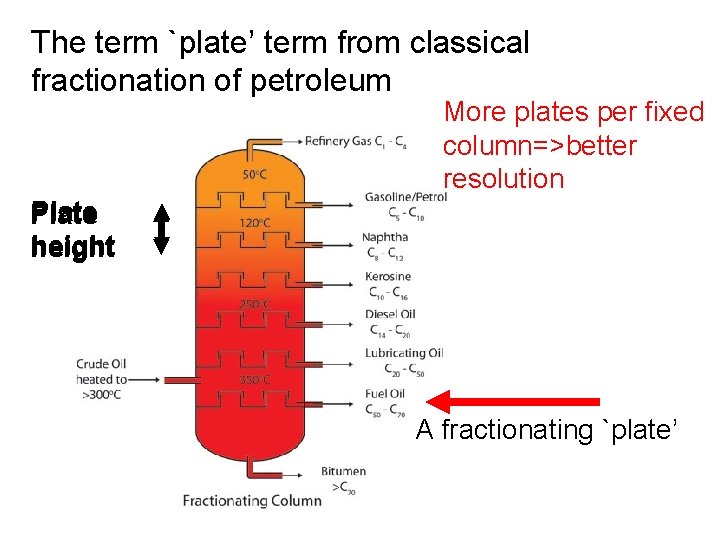
The term `plate’ term from classical fractionation of petroleum More plates per fixed column=>better resolution Plate height A fractionating `plate’

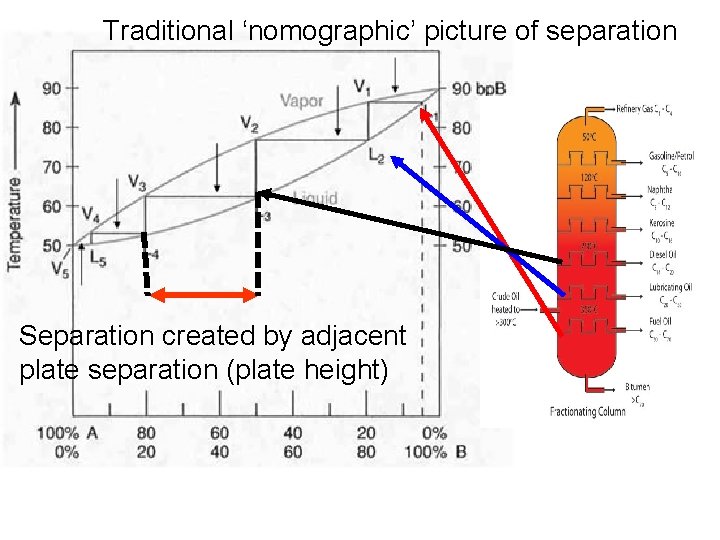
Traditional ‘nomographic’ picture of separation Separation created by adjacent plate separation (plate height)

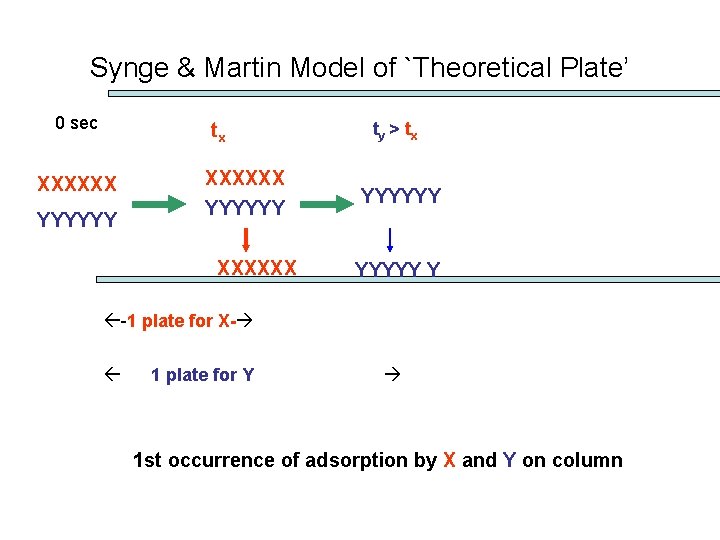
An atomic scale model of this process was developed by Synge and Martin, who won the only Nobel Prize ever awarded for separation science

Synge & Martin Model of `Theoretical Plate’ 0 sec tx XXXXXX YYYYYY XXXXXX ty > tx YYYYYY Y -1 plate for X- 1 plate for Y 1 st occurrence of adsorption by X and Y on column

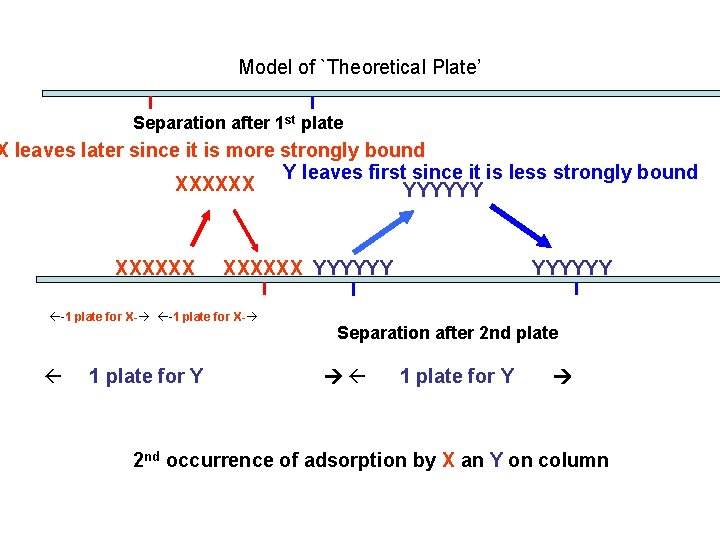
Model of `Theoretical Plate’ Separation after 1 st plate X leaves later since it is more strongly bound Y leaves first since it is less strongly bound XXXXXX YYYYYY -1 plate for X- 1 plate for Y YYYYYY Separation after 2 nd plate 1 plate for Y 2 nd occurrence of adsorption by X an Y on column

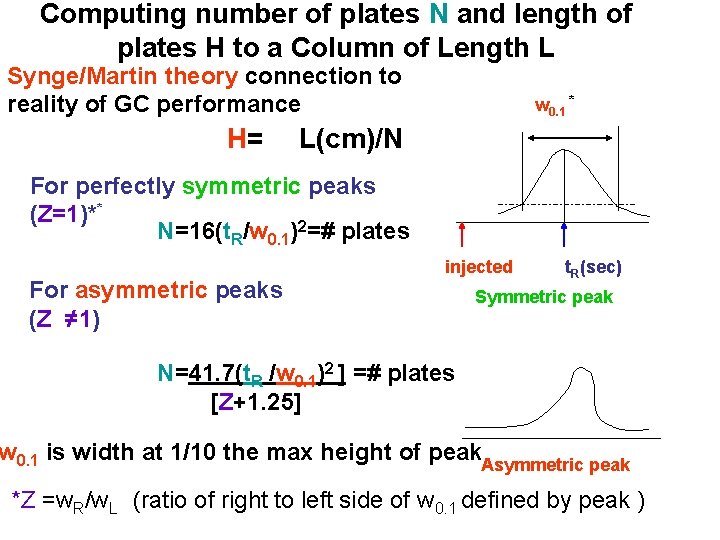
Computing number of plates N and length of plates H to a Column of Length L Synge/Martin theory connection to reality of GC performance H= w 0. 1 * L(cm)/N For perfectly symmetric peaks (Z=1)** N=16(t. R/w 0. 1)2=# plates For asymmetric peaks (Z ≠ 1) injected t. R(sec) Symmetric peak N=41. 7(t. R /w 0. 1)2 ] =# plates [Z+1. 25] w 0. 1 is width at 1/10 the max height of peak. Asymmetric peak *Z =w. R/w. L (ratio of right to left side of w 0. 1 defined by peak )

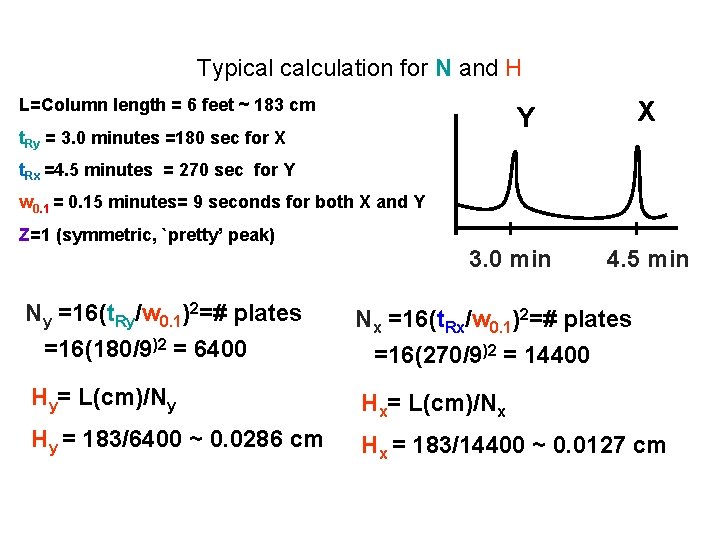
Typical calculation for N and H L=Column length = 6 feet ~ 183 cm X Y t. Ry = 3. 0 minutes =180 sec for X t. Rx =4. 5 minutes = 270 sec for Y w 0. 1 = 0. 15 minutes= 9 seconds for both X and Y Z=1 (symmetric, `pretty’ peak) 3. 0 min Ny =16(t. Ry/w 0. 1)2=# plates =16(180/9)2 = 6400 4. 5 min Nx =16(t. Rx/w 0. 1)2=# plates =16(270/9)2 = 14400 Hy= L(cm)/Ny Hx= L(cm)/Nx Hy = 183/6400 ~ 0. 0286 cm Hx = 183/14400 ~ 0. 0127 cm

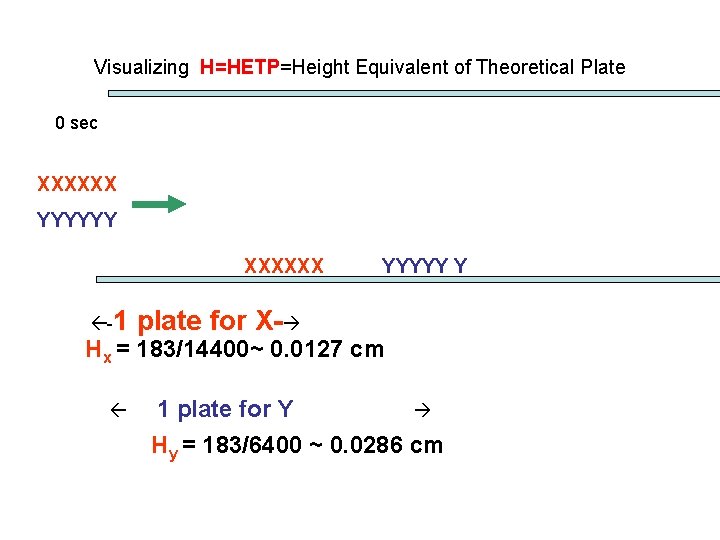
Visualizing H=HETP=Height Equivalent of Theoretical Plate 0 sec XXXXXX YYYYYY XXXXXX -1 YYYYY Y plate for X- Hx = 183/14400~ 0. 0127 cm 1 plate for Y Hy = 183/6400 ~ 0. 0286 cm

Now that I’ve set the table about plates…let’s work some problems using the model: Exercise 4