Theoretical Mechanics 6 The plane parallel motion of

Theoretical Mechanics 6. The plane parallel motion of the rigid body (Plane kinematics of rigid bodies) Lecture 5. Kinematics of the rigid body 1

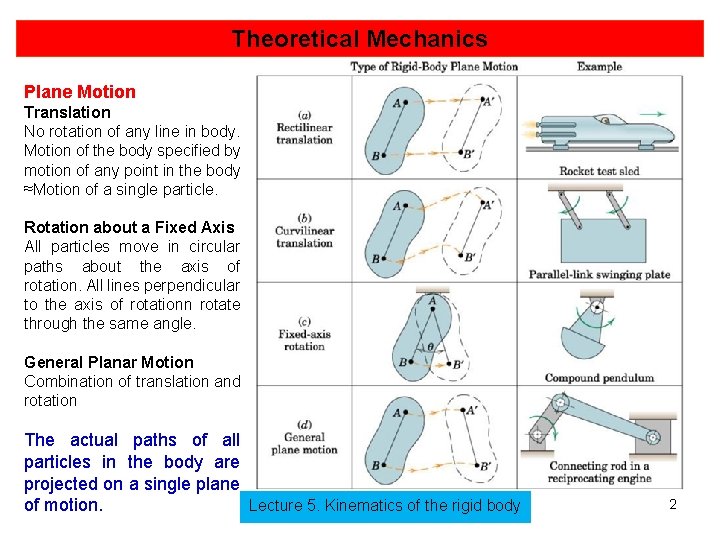
Theoretical Mechanics Plane Motion Translation No rotation of any line in body. Motion of the body specified by motion of any point in the body ≈Motion of a single particle. Rotation about a Fixed Axis All particles move in circular paths about the axis of rotation. All lines perpendicular to the axis of rotationn rotate through the same angle. General Planar Motion Combination of translation and rotation The actual paths of all particles in the body are projected on a single plane Lecture 5. Kinematics of the rigid body of motion. 2

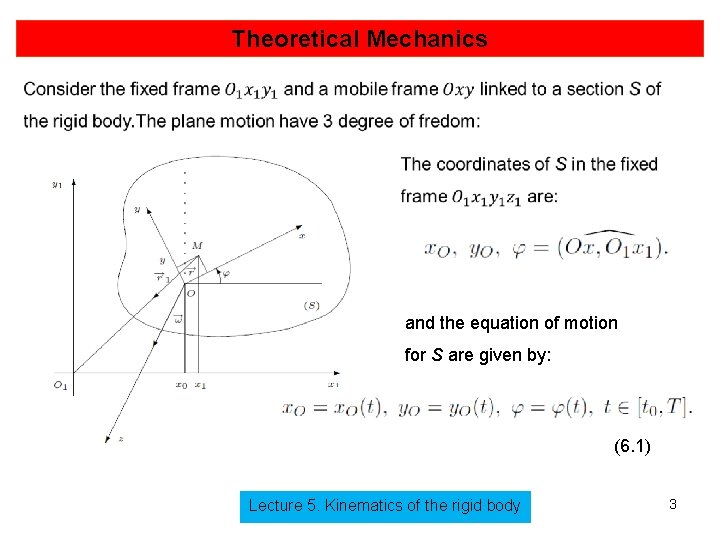
Theoretical Mechanics and the equation of motion for S are given by: (6. 1) Lecture 5. Kinematics of the rigid body 3

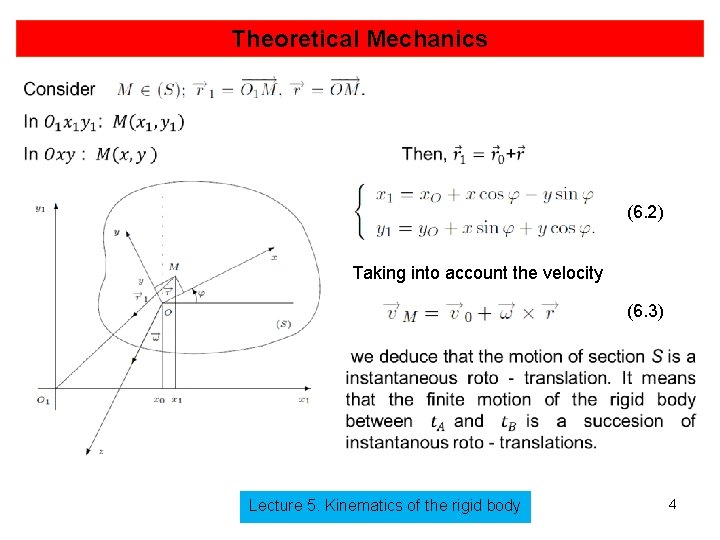
Theoretical Mechanics (6. 2) Taking into account the velocity (6. 3) Lecture 5. Kinematics of the rigid body 4

Theoretical Mechanics Moreover, (6. 4) (6. 5) Lecture 5. Kinematics of the rigid body 5

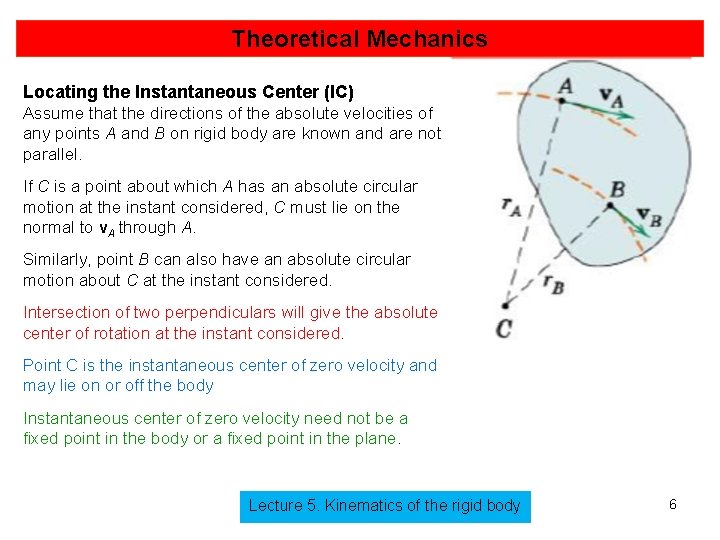
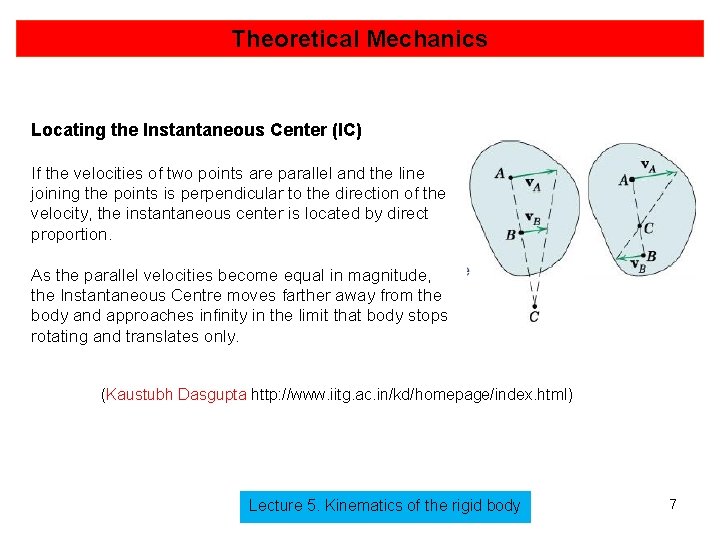
Theoretical Mechanics Locating the Instantaneous Center (IC) Assume that the directions of the absolute velocities of any points A and B on rigid body are known and are not parallel. If C is a point about which A has an absolute circular motion at the instant considered, C must lie on the normal to v. A through A. Similarly, point B can also have an absolute circular motion about C at the instant considered. Intersection of two perpendiculars will give the absolute center of rotation at the instant considered. Point C is the instantaneous center of zero velocity and may lie on or off the body Instantaneous center of zero velocity need not be a fixed point in the body or a fixed point in the plane. Lecture 5. Kinematics of the rigid body 6

Theoretical Mechanics Locating the Instantaneous Center (IC) If the velocities of two points are parallel and the line joining the points is perpendicular to the direction of the velocity, the instantaneous center is located by direct proportion. As the parallel velocities become equal in magnitude, the Instantaneous Centre moves farther away from the body and approaches infinity in the limit that body stops rotating and translates only. (Kaustubh Dasgupta http: //www. iitg. ac. in/kd/homepage/index. html) Lecture 5. Kinematics of the rigid body 7

Theoretical Mechanics (6. 5) (6. 6) Thus, we obtain: (6. 7) (6. 8) If magnitude of velocity at one of the points on the rigid body under general plane motion is known (v. A) the angular velocity of the body ω and linear velocity of every point in the body can be easily obtained using: ω= v. A/ r. A Velocity of B is v. B= r. Bω= (r. B/r. A) v. A. Lecture 5. Kinematics of the rigid body 8

Theoretical Mechanics Once the IC is located, the direction of the instantaneous velocity of every point in the body is readily found since it must be perpendicular to the radial line joining the point in question with IC. Velocity of all such points: v= rω Note that the spokes are somewhat visible near IC, whereas at the top of the wheel they become blurred. Also note how the direction of velocity varies at different point on the rim of the wheel. Lecture 5. Kinematics of the rigid body 9

Theoretical Mechanics Lecture 5. Kinematics of the rigid body 10

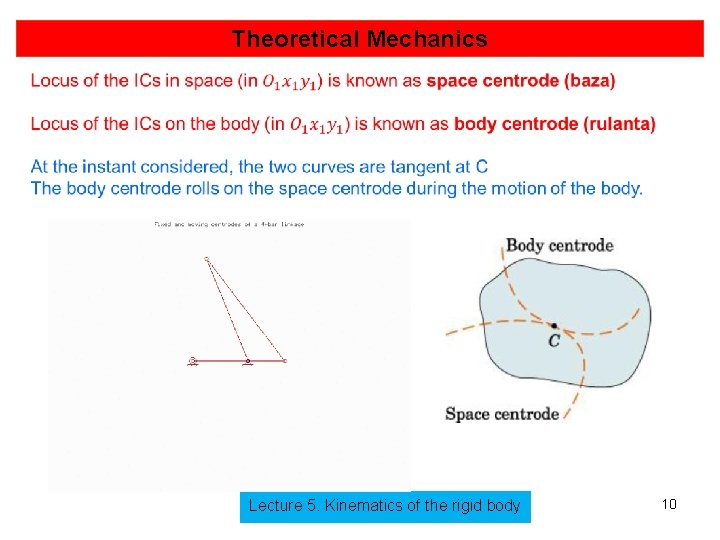
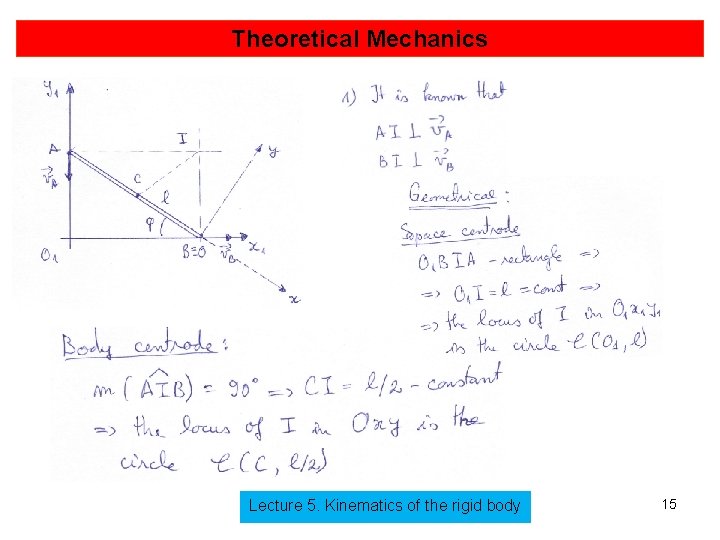
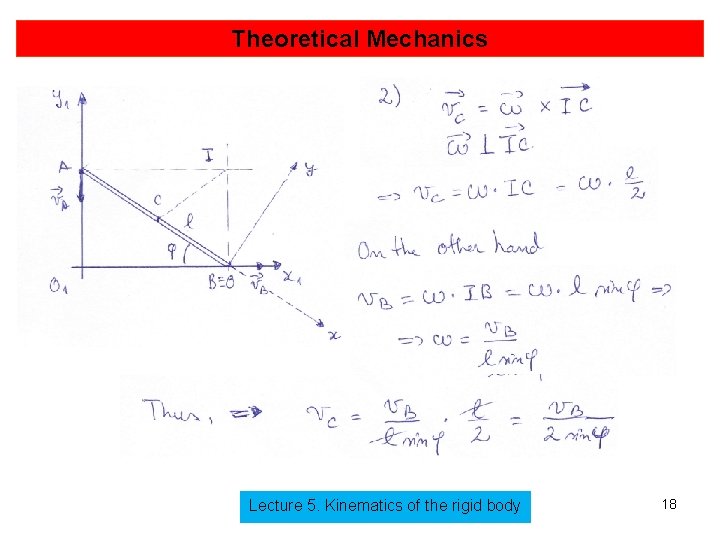
Theoretical Mechanics Further, we deduce the equations of the space and body centrode: (6. 9) But and using (6. 9) we have (6. 10) Lecture 5. Kinematics of the rigid body 11

Theoretical Mechanics On the other hand, Thus (6. 11) Lecture 5. Kinematics of the rigid body 12

Theoretical Mechanics Using (6. 11) and taking into account we have (6. 12) Lecture 5. Kinematics of the rigid body 13

Theoretical Mechanics Lecture 5. Kinematics of the rigid body 14

Theoretical Mechanics Lecture 5. Kinematics of the rigid body 15

Theoretical Mechanics Lecture 5. Kinematics of the rigid body 16

Theoretical Mechanics Lecture 5. Kinematics of the rigid body 17

Theoretical Mechanics Lecture 5. Kinematics of the rigid body 18

Theoretical Mechanics 7. Relative motion of the particle Consider a particle M moving in a refernce frame Oxyz. The reference frame Oxyz is moving relative to a fixed frame O 1 x 1 y 1 z 1. Lecture 5. Kinematics of the rigid body 19

Theoretical Mechanics Consider a particle M moving in a reference frame Oxyz and the reference frame Oxyz is moving relative to a fixed frame O 1 x 1 y 1 z 1. (7. 1) (7. 2) Lecture 5. Kinematics of the rigid body 20

Theoretical Mechanics Consider the position vector of M: (7. 3) Velocity: (7. 4) Lecture 5. Kinematics of the rigid body 21

Theoretical Mechanics The term (7. 5) The term (7. 6) Using (7. 4) -(7. 6) we can give the first Coriolis formula: (7. 7) The absolute velocity is the sum of the relative and transport velocity. Lecture 5. Kinematics of the rigid body 22

Theoretical Mechanics Acceleration = = (7. 8) Here is the absolute acceleration, Lecture 5. Kinematics of the rigid body 23

Theoretical Mechanics (7. 9) is the relative acceleration, (7. 10) is the transport acceleration, and (7. 11) is the Coriolis acceleration. The second Coriolis formula is given by: (7. 12) Lecture 5. Kinematics of the rigid body 24

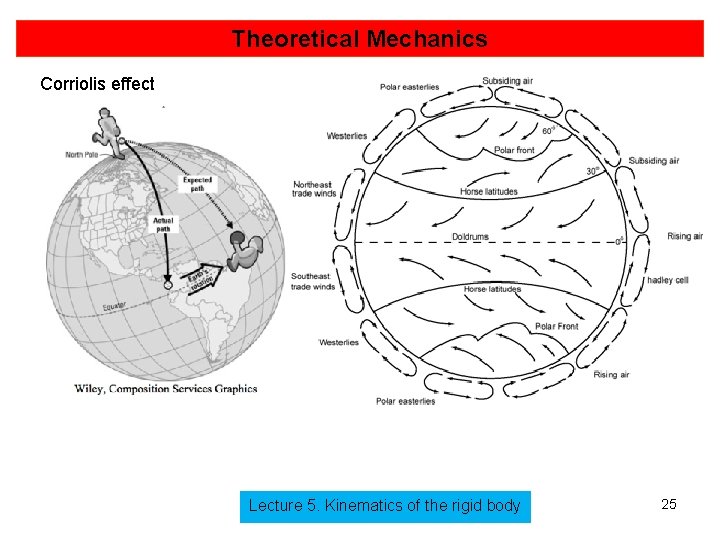
Theoretical Mechanics Corriolis effect Lecture 5. Kinematics of the rigid body 25

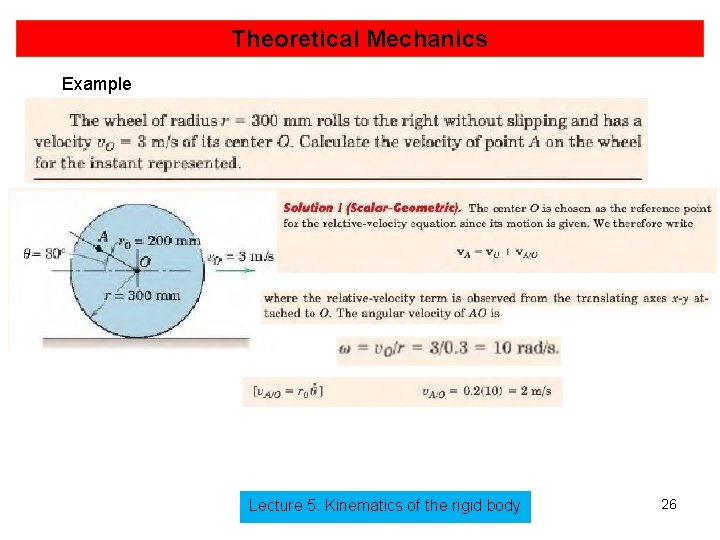
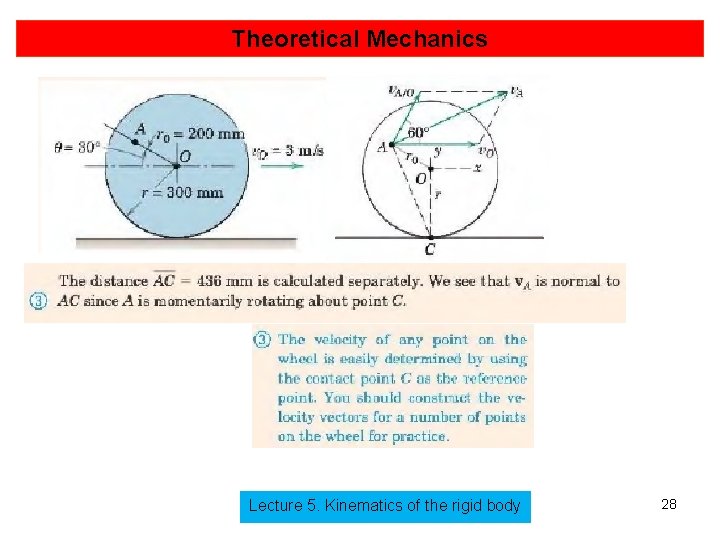
Theoretical Mechanics Example Lecture 5. Kinematics of the rigid body 26

Theoretical Mechanics Lecture 5. Kinematics of the rigid body 27

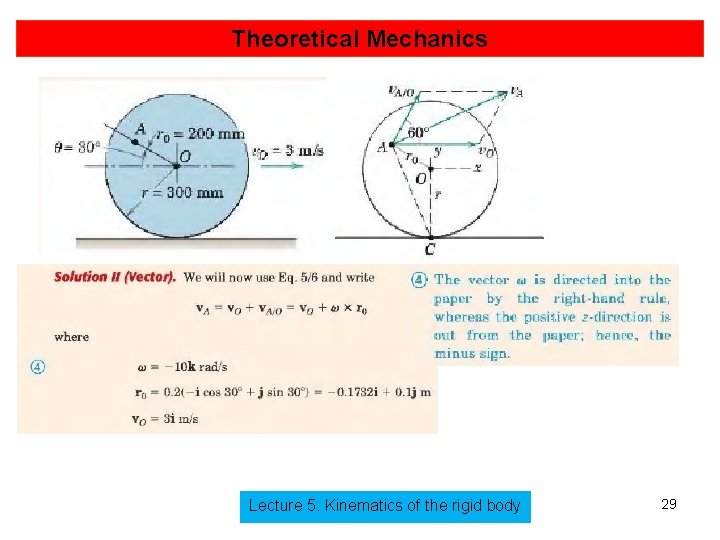
Theoretical Mechanics Lecture 5. Kinematics of the rigid body 28

Theoretical Mechanics Lecture 5. Kinematics of the rigid body 29

Theoretical Mechanics Lecture 5. Kinematics of the rigid body 30