Theoretical community models Incorporating dispersal Community consequences of

Theoretical community models: Incorporating dispersal

Community consequences of dispersal • Dispersal brings new species • Dispersal allows persistence in unsuitable habitat (“sinks”) • Dispersal can counteract (or reinforce) local selection • Dispersal can counteract drift (flipside: limited dispersal allows communities to drift apart) • If dispersal ability is negatively correlated with competitive ability (i. e. , there is a tradeoff) across species, stable coexistence can be maintained

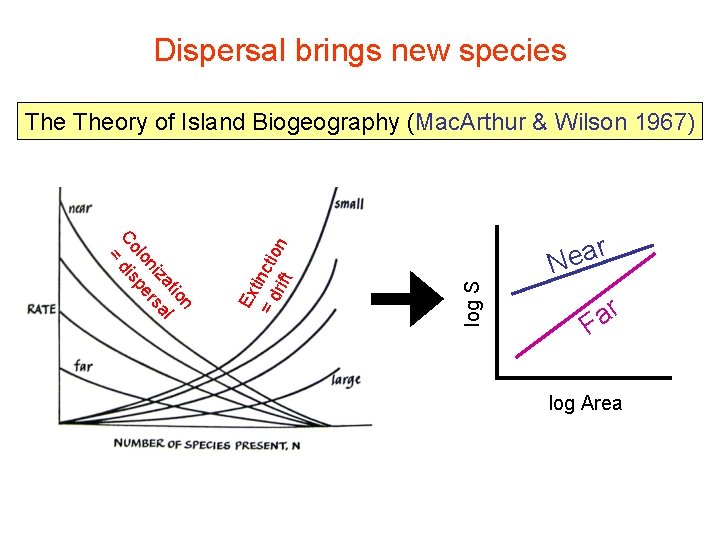
Dispersal brings new species r a e N log S n tio l za a ni rs lo pe Co dis = Ex t = d inctio rift n Theory of Island Biogeography (Mac. Arthur & Wilson 1967) r a F log Area

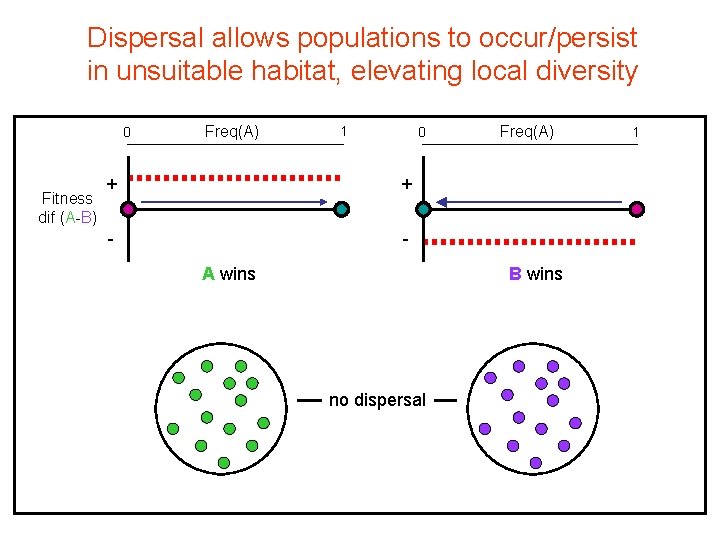
Dispersal allows populations to occur/persist in unsuitable habitat, elevating local diversity 0 Fitness dif (A-B) Freq(A) 1 0 + + - A wins Freq(A) B wins no dispersal 1

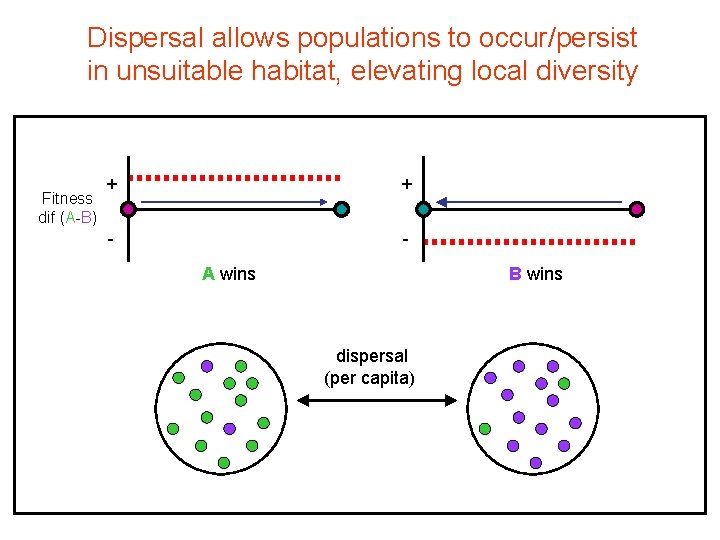
Dispersal allows populations to occur/persist in unsuitable habitat, elevating local diversity Fitness dif (A-B) + + - A wins B wins dispersal (per capita)

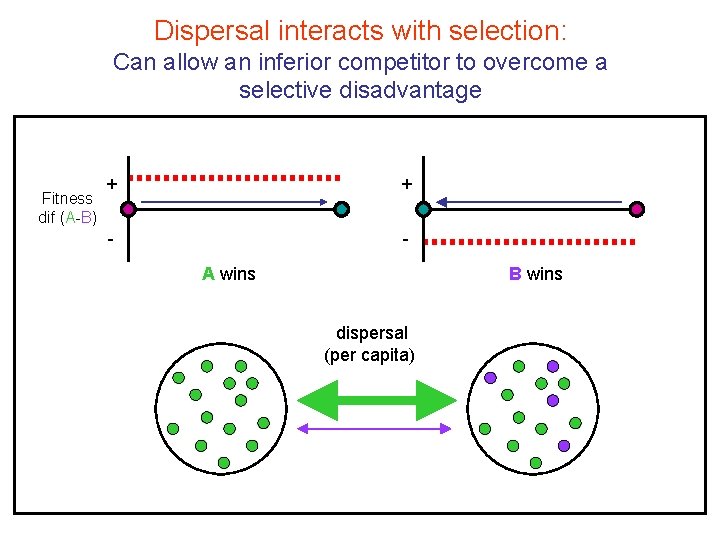
Dispersal interacts with selection: Can allow an inferior competitor to overcome a selective disadvantage Fitness dif (A-B) + + - A wins B wins dispersal (per capita)

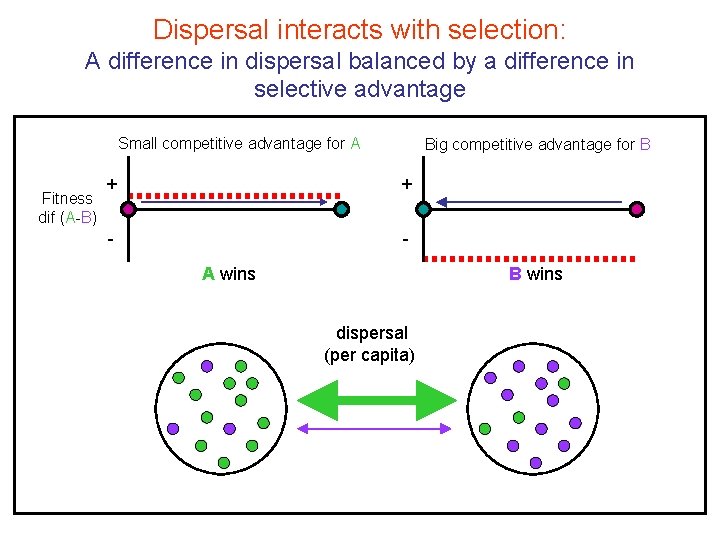
Dispersal interacts with selection: A difference in dispersal balanced by a difference in selective advantage Small competitive advantage for A Fitness dif (A-B) Big competitive advantage for B + + - A wins B wins dispersal (per capita)

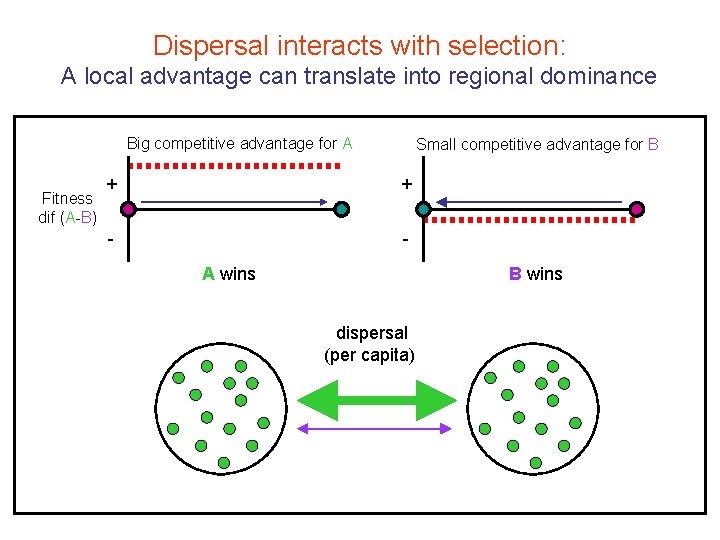
Dispersal interacts with selection: A local advantage can translate into regional dominance Big competitive advantage for A Fitness dif (A-B) Small competitive advantage for B + + - A wins B wins dispersal (per capita)

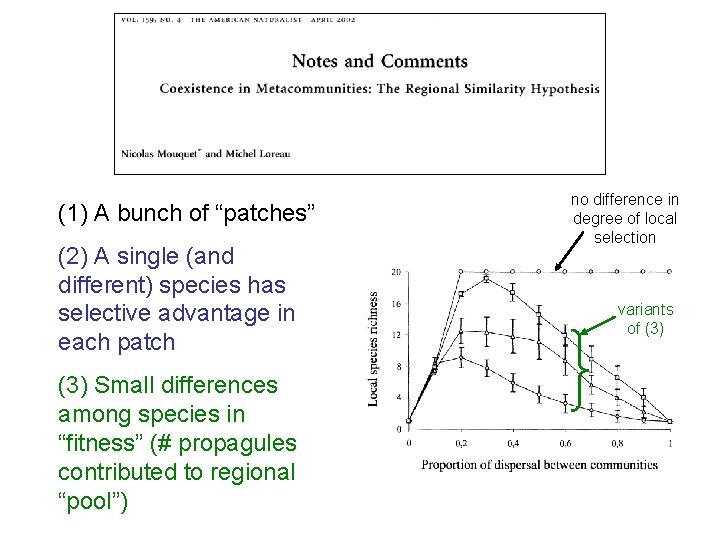
(1) A bunch of “patches” (2) A single (and different) species has selective advantage in each patch (3) Small differences among species in “fitness” (# propagules contributed to regional “pool”) no difference in degree of local selection variants of (3)

# Set initial communities (e. g. , 25 individuals of sp. 1 + 25 of sp. 2; J = 50) J <- 50 # must be an even number COMa <- vector(length=J) COMa[1: J/2] <- 1 COMa[(J/2+1): J] <- 2 COMb <- vector(length=J) COMb[1: J/2] <- 1 COMb[(J/2+1): J] <- 2 # dispersal rate m <- 0. 2 Limited dispersal allows drift to create differences between communities # set number of “years” to run simulations & empty matrix for data num_years <- 50 prop_1 <- matrix(0, nrow=J* num_years, ncol=2) # run model for (i in 1: (J*num_years)) { # chose cell for death_cell <- ceiling(J*runif(1)) # pick randomly between two sites for a death; chose replacer from # other site with probability m; from same site with probability (1 -m) if (runif(1) > 0. 5) { if (runif(1) > m) COMa[death_cell] <- COMa[ceiling(J*runif(1))] else COMa[death_cell] <- COMb[ceiling(J*runif(1))] } else { if (runif(1) > m) COMb[death_cell] <- COMb[ceiling(J*runif(1))] else COMb[death_cell] <- COMa[ceiling(J*runif(1))] } prop_1[i, 1] <- sum(COMa==1)/J prop_1[i, 2] <- sum(COMb==1)/J }

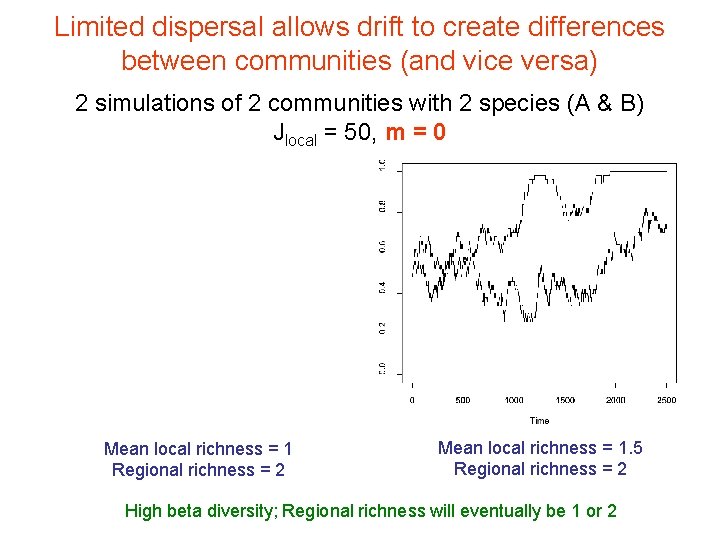
Limited dispersal allows drift to create differences between communities (and vice versa) 2 simulations of 2 communities with 2 species (A & B) Jlocal = 50, m = 0 Mean local richness = 1 Regional richness = 2 Mean local richness = 1. 5 Regional richness = 2 High beta diversity; Regional richness will eventually be 1 or 2

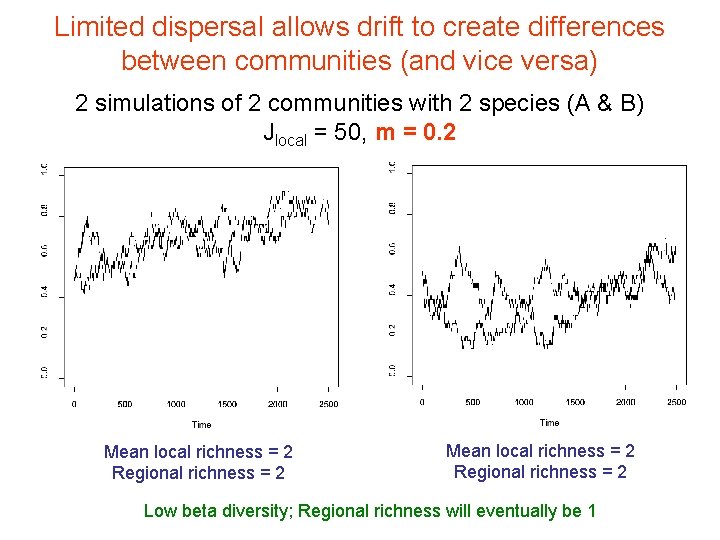
Limited dispersal allows drift to create differences between communities (and vice versa) 2 simulations of 2 communities with 2 species (A & B) Jlocal = 50, m = 0. 2 Mean local richness = 2 Regional richness = 2 Low beta diversity; Regional richness will eventually be 1

Stable coexistence can be maintained if there is a trade-off among species between competitive ability and colonization ability Pseudo-code for 2 species A is a good disperser & poor competitor; B is the opposite for loop Kill a bunch of individuals Each species sends out a bunch of dispersers (A > B, per capita) If A lands in an empty cell, it occupies it If A lands in a B cell, it dies If A lands in an A cell, non-event If B lands in an empty cell, it dies (or has low prob of occupying it) If B lands in an A cell, it kicks out A and occupies the cell If B lands in a B cell, non-event stop for loop

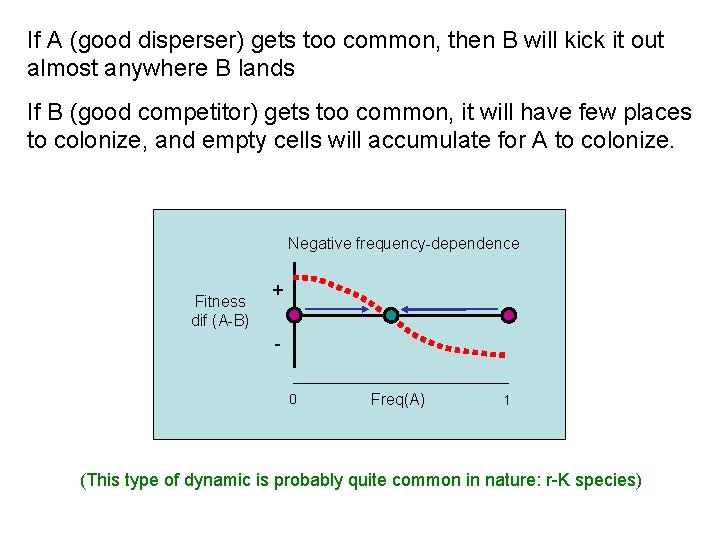
If A (good disperser) gets too common, then B will kick it out almost anywhere B lands If B (good competitor) gets too common, it will have few places to colonize, and empty cells will accumulate for A to colonize. Negative frequency-dependence Fitness dif (A-B) + 0 Freq(A) 1 (This type of dynamic is probably quite common in nature: r-K species)

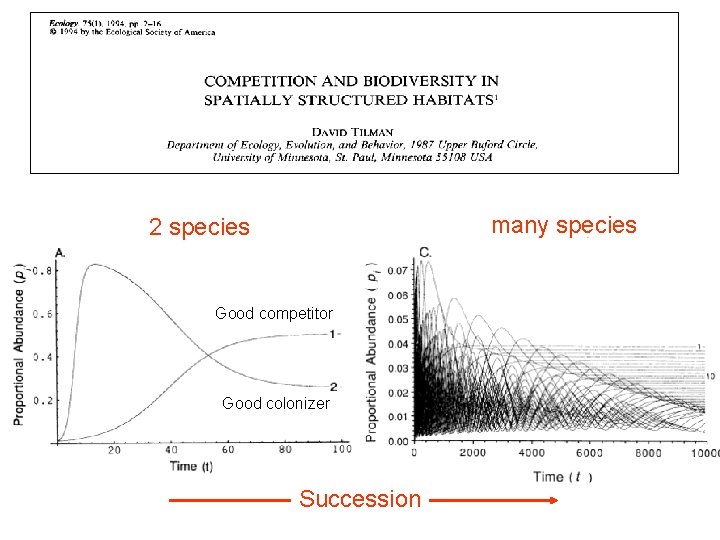
many species 2 species Good competitor Good colonizer Succession

- Predators cause prey to go locally extinct, which in turn causes predator to go extinct - Prey better at getting to empty sites - Predators “chase” prey through space, but prey stay one step ahead = stable coexistence

Is the effect of dispersal on communities stochastic? The trajectory of community dynamics (abundances of multiple species) can be greatly changed colonization order or by the presence/absence of particular species We don’t know who’s coming next (i. e. , arriving via dispersal) Therefore, the effect of dispersal on communities is (partly) stochastic

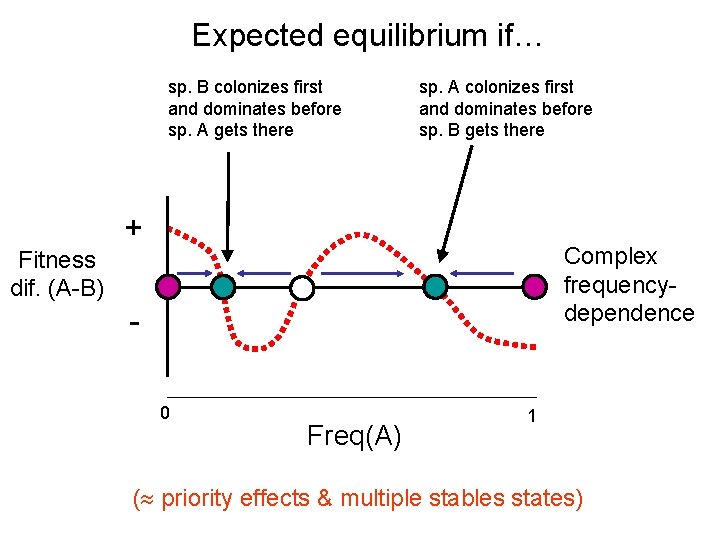
Expected equilibrium if… sp. B colonizes first and dominates before sp. A gets there sp. A colonizes first and dominates before sp. B gets there + Complex frequencydependence Fitness dif. (A-B) 0 Freq(A) 1 ( priority effects & multiple stables states)

A framework for incorporating dispersal into community ecology Leibold et al. (2004, Ecology Letters)

The metacommunity framework (examples with 2 competing species, 3 patches) Patch dynamics (showing competitioncolonization tradeoff) Dispersal + Selection (freq. dependent locally) Mass effects As in (b) but with higher dispersal Leibold et al. (2004, Ecology Letters) Species sorting Dispersal + Selection (constant locally, spatially heterogeneous) Neutral Dispersal + drift

Key questions for determining community consequences of dispersal: (1) The composition of the dispersers (2) The selection/drift regime where the dispersers arrive