Theorems on Redundancy Identification Vishal J Mehta Vishwani

Theorems on Redundancy Identification Vishal J. Mehta Vishwani D. Agrawal Michael L. Bushnell Rutgers University, ECE Dept. Piscataway, New Jersey, USA 9/24/2021 Mehta et al. : Redundancy theorems 1

Talk Outline • Introduction • Problem statement • Prior work • Primary contribution • Completion of previous implementation • Fixed-value theorem • Stem unobservability theorems • Results and conclusion 9/24/2021 Mehta et al. : Redundancy theorems 2

Problem Statement For identifying logic redundancy: • Implement the implication graph and transitive closure procedures with direct and partial implications. • Enhance transitive closure for contrapositive implications and fixed -valued signals. • Find new ways to Identify unobservable fanout stems. 9/24/2021 Mehta et al. : Redundancy theorems 3

Prior Work on Redundancy • • • Automatic Test Pattern Generation (ATPG) • Uses exhaustive test pattern generation to determine whether or not a target fault has a test. • Can identify all redundancies -- exponential complexity. • Boolean satisfiability methods use logic implications: Chakradhar et al. , Larrabee, Henftling et al. , Zhao et al. , etc. . Testability analysis (fault-independent) • Mostly approximate, linear complexity • Raitu et al. , Goldstein, Seth and Agrawal, etc. Fault-independent redundancy identification • Implication analysis identifies all or a subset of redundant faults -- polynomial complexity (empirically linear). • Agrawal et al. , Gaur et al. , Iyer and Abramovici, etc. 9/24/2021 Mehta et al. : Redundancy theorems 4

Fault-Independent Methods • Iyer and Abramovici (IEEE-TC, June 1996) use • • implications to find redundant faults whose tests require contradictory values on a signal. Agrawal et al. (ATS’ 96) use implication graph, introduce observability variables, and use transitive closure for redundancy identification. Gaur et al. (DELTA’ 02) include anding nodes to represent higher-order implications among signals and observability variables. 9/24/2021 Mehta et al. : Redundancy theorems 5

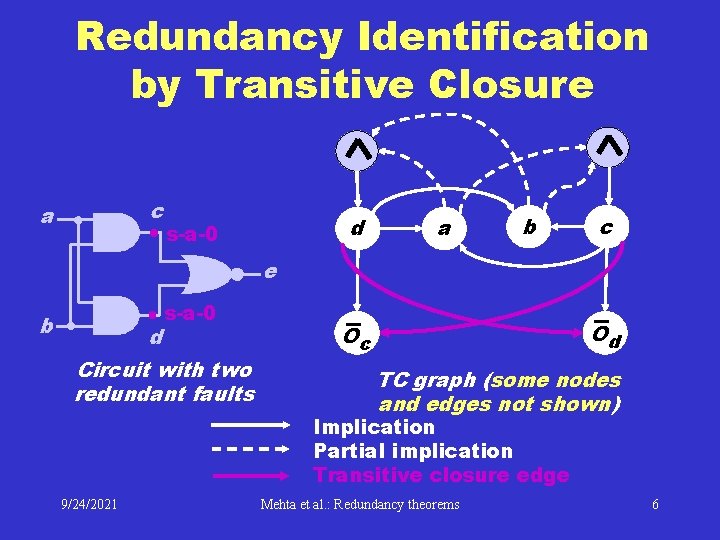
Redundancy Identification by Transitive Closure c a d s-a-0 a b c e b d s-a-0 Circuit with two redundant faults Od Oc TC graph (some nodes and edges not shown) Implication Partial implication Transitive closure edge 9/24/2021 Mehta et al. : Redundancy theorems 6

Method Summarized • Obtain an implication graph from the circuit • • topology and compute transitive closure. There are 8 different conditions on the basis of which a fault is identified to be redundant. Examples: • • If node c implies c then line c is fixed at 0 and s-a-0 fault on it is redundant. If node Oc implies Oc then line c is unobservable and both s-a-0 and s-a-1 faults on it are redundant. • These conditions obey the contrapositive rule. 9/24/2021 Mehta et al. : Redundancy theorems 7

Talk Outline • Introduction • Problem statement • Prior work • Primary contribution • Completion of previous implementation • Fixed-value theorem • Stem unobservability theorems • Results and conclusion 9/24/2021 Mehta et al. : Redundancy theorems 8

Motivation • Incomplete implementation (Gaur et al. ) • Only few anding nodes implemented • Some direct implications missing • Not all contrapositive relations determined by transitive closure • Effect of fixed-valued nodes not included in transitive closure • No observability relation across fanouts • Redundancies due to stem unobservability not identified 9/24/2021 Mehta et al. : Redundancy theorems 9

Completion of Previous Implementation • Only one of the possible (n+1) signal anding nodes were implemented by Gaur et al. • None of the possible n(n+1) observability anding nodes were implemented. • Some direct implications for observability variables were not implemented. 9/24/2021 Mehta et al. : Redundancy theorems 10

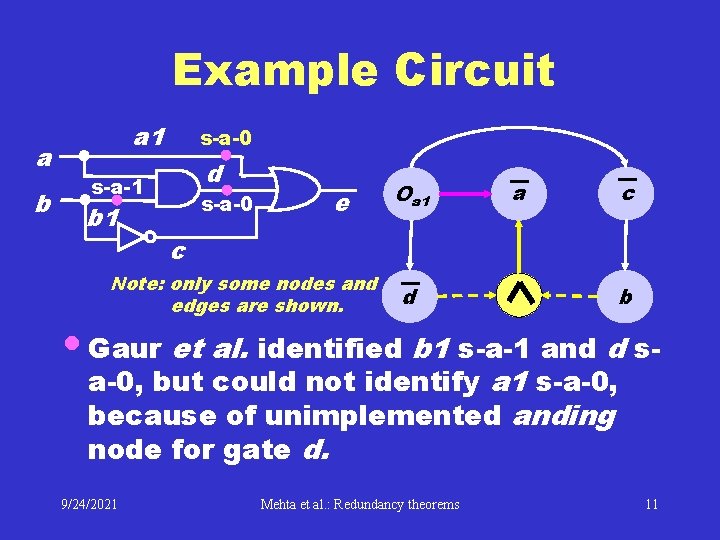
Example Circuit a b a 1 s-a-0 d s-a-1 b 1 s-a-0 e Oa 1 a c c Note: only some nodes and edges are shown. d b • Gaur et al. identified b 1 s-a-1 and d sa-0, but could not identify a 1 s-a-0, because of unimplemented anding node for gate d. 9/24/2021 Mehta et al. : Redundancy theorems 11

Fixed-Value Theorem • If a Boolean variable in the implication graph is fixed to a true (false) value then there exist unconditional edges from all other nodes in the graph to the node representing the true (false) state of the fixed variable. 9/24/2021 Mehta et al. : Redundancy theorems 12

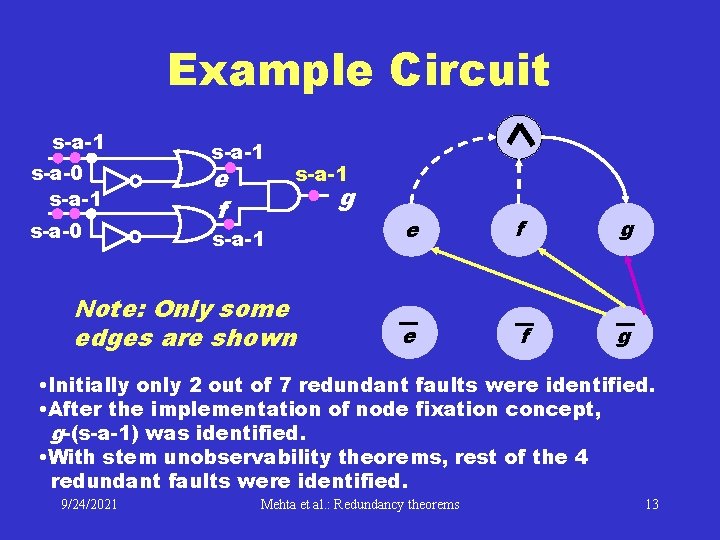
Example Circuit s-a-1 s-a-0 s-a-1 e f s-a-1 g s-a-1 Note: Only some edges are shown e f g • Initially only 2 out of 7 redundant faults were identified. • After the implementation of node fixation concept, g-(s-a-1) was identified. • With stem unobservability theorems, rest of the 4 redundant faults were identified. 9/24/2021 Mehta et al. : Redundancy theorems 13

Stem Unobservability Theorem 1 • A fanout stem is unobservable, if each signal in its dominator set assumes a constant value and: • either the fanout stem does not hold a constant value • or the fanout stem holds a constant value and, in spite of any local change in the stem signal, the dominator set values do not change. Notes: • A local change of a signal only affects the portion of the circuit between that signal and POs. • Dominator set is the set of signals through which a signal in the circuit should pass in order to reach the primary output. 9/24/2021 Mehta et al. : Redundancy theorems 14

Example Circuit a b c unobs. stem 1 fixed dom. d • For the fanout stem b, the dominator signal d is fixed to 1. • As b is not fixed, Theorem 1 identifies b as unobservable stem. 9/24/2021 Mehta et al. : Redundancy theorems 15

Theorem 2 • A fanout stem is unobservable, if each signal in its dominator set is unobservable and: • either the stem does not hold a constant value • or the stem holds a constant value and, in spite of any local change in the stem signal, the unobservable status of the dominator set remains unchanged. Note: A lemma by Iyer and Abramovici is a special case of Theorem 2. 9/24/2021 Mehta et al. : Redundancy theorems 16

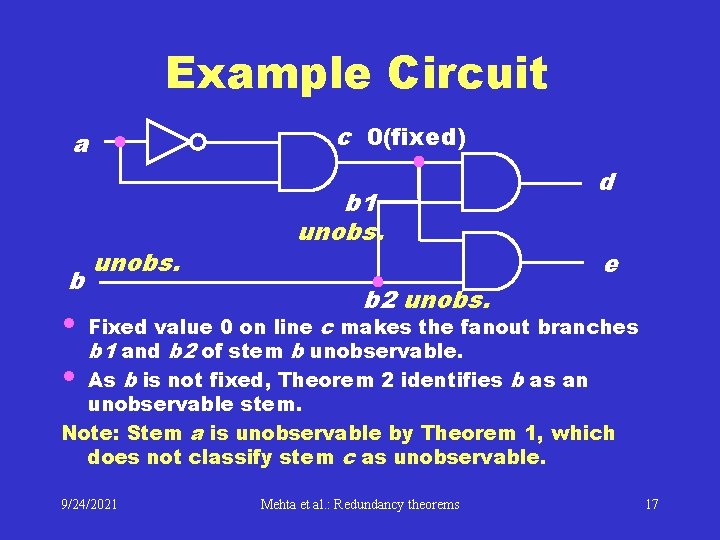
Example Circuit c 0(fixed) a b unobs. • b 1 unobs. d e b 2 unobs. Fixed value 0 on line c makes the fanout branches b 1 and b 2 of stem b unobservable. • As b is not fixed, Theorem 2 identifies b as an unobservable stem. Note: Stem a is unobservable by Theorem 1, which does not classify stem c as unobservable. 9/24/2021 Mehta et al. : Redundancy theorems 17

Talk Outline • Introduction • Problem statement • Prior work • Primary contribution • Completion of previous implementation • Fixed-value theorem • Stem unobservability theorems • Results and conclusion 9/24/2021 Mehta et al. : Redundancy theorems 18

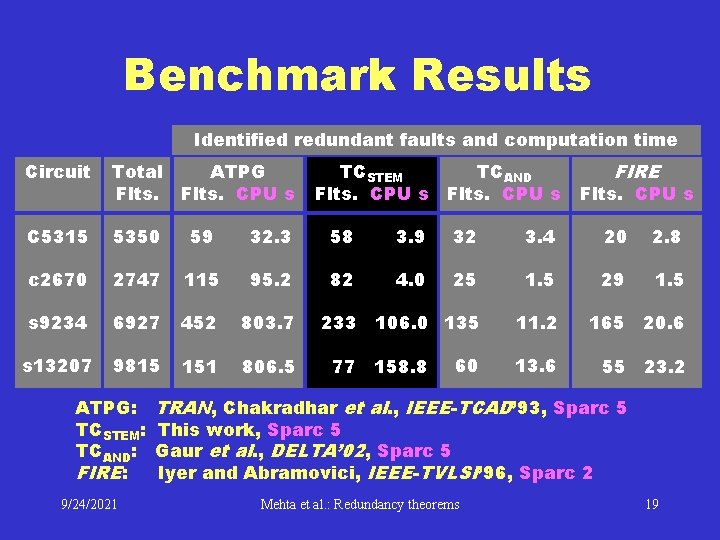
Benchmark Results Identified redundant faults and computation time Total Flts. C 5315 5350 59 32. 3 58 3. 9 32 3. 4 20 2. 8 c 2670 2747 115 95. 2 82 4. 0 25 1. 5 29 1. 5 s 9234 s s 13207 6927 9 9815 452 803. 7 233 106. 0 135 11. 2 165 20. 6 151 806. 5 60 13. 6 55 23. 2 ATPG: TCSTEM: TCAND: FIRE: 9/24/2021 ATPG Flts. CPU s TCSTEM Flts. CPU s 77 158. 8 TCAND Flts. CPU s FIRE Circuit Flts. CPU s TRAN, Chakradhar et al. , IEEE-TCAD’ 93, Sparc 5 This work, Sparc 5 Gaur et al. , DELTA’ 02, Sparc 5 Iyer and Abramovici, IEEE-TVLSI’ 96, Sparc 2 Mehta et al. : Redundancy theorems 19

Limitations of Method unobs. stem a d a f e Example 1 • • e s-a-1 c b s-a-1 f b s-a-0 d s-a-1 c h g Example 2 Example 1: None of the stem unobservability theorems can identify stem a as unobservable because the dominator set is neither fixed nor unobservable. Example 2: e s-a-1 is redundant because f=g=1 require b=0, which implies e=1. Because f=1 and g=1 are separately treated in the transitive closure and each has multiple satisfying choices, the essential requirement b=0 is not found. The method fails to find this redundancy. 9/24/2021 Mehta et al. : Redundancy theorems 20

Conclusion • Partial implications, fixed-value theorem and • • • stem unobservability theorems improve the process of redundant fault identification better than any other known fault-independent technique. Checking for the contrapositive rule to update transitive closure may have benefits. A demonstrated limitation of stem unobservability theorems can be improved upon. Possible ways to find essential signal assignments caused by combinations of multiple signals may provide further improvements. 9/24/2021 Mehta et al. : Redundancy theorems 21

Future Work • Various applications of the TC technique can be explored: • Identifying equivalent faults • Checking equivalence of combinational circuits. • 2 and 3 valued logic simulators. 9/24/2021 Mehta et al. : Redundancy theorems 22

THANK YOU 9/24/2021 Mehta et al. : Redundancy theorems 23