Theorem Pythagorean Theorem c a b a b

Theorem Pythagorean Theorem

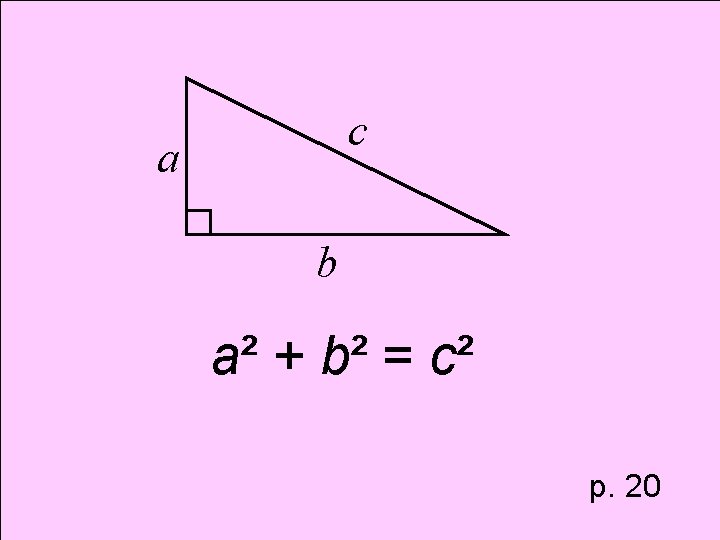
c a b a² + b² = c² p. 20

Theorem Distance Formula

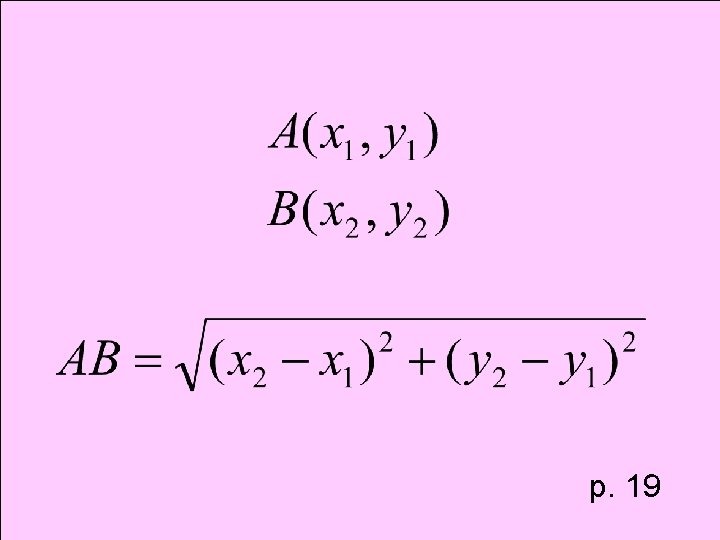
p. 19

Postulate Segment Addition Postulate

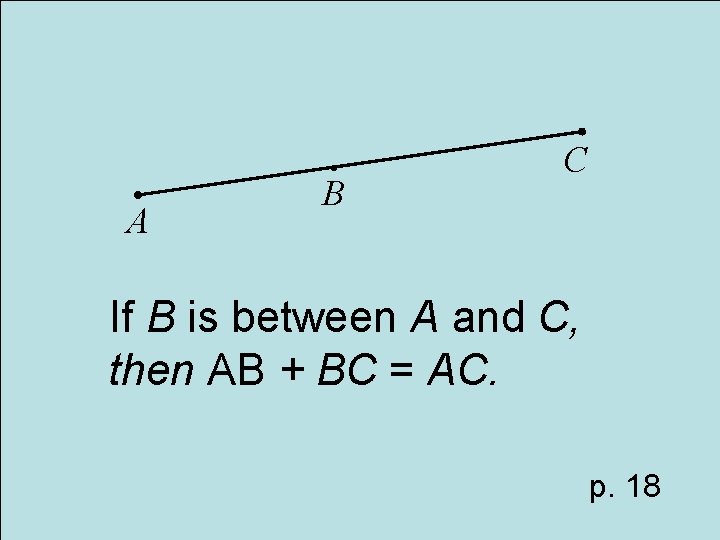
A B C If B is between A and C, then AB + BC = AC. p. 18

Postulate Angle Addition Postulate

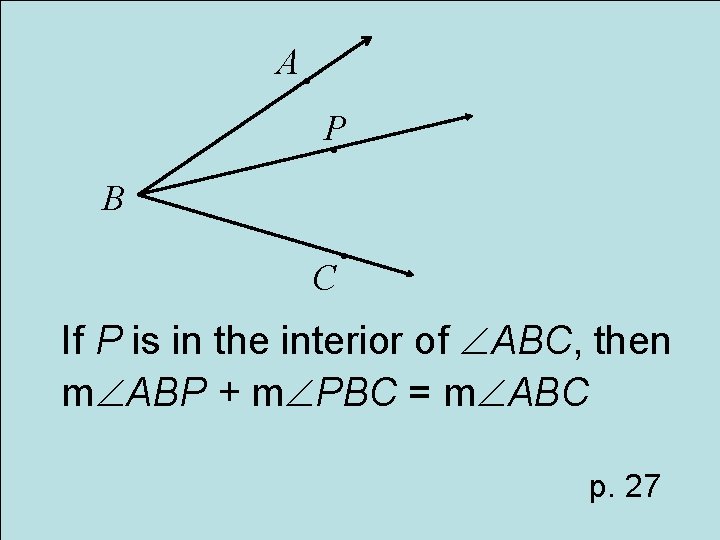
A P B C If P is in the interior of ABC, then m ABP + m PBC = m ABC p. 27

Definition midpoint

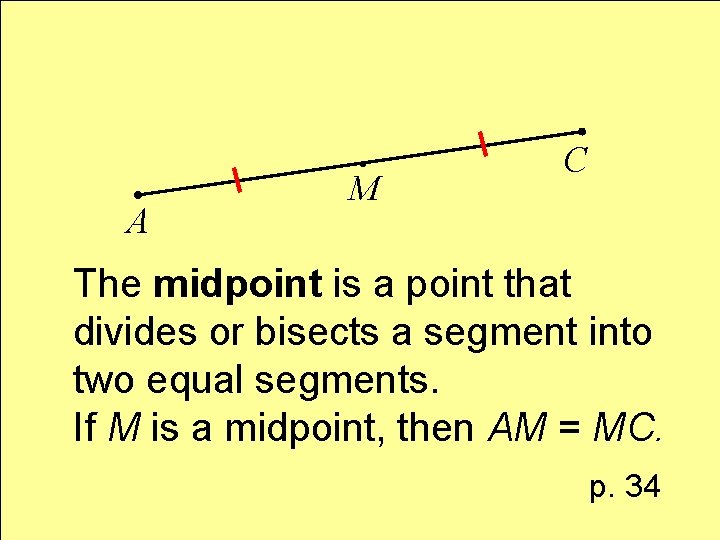
A M C The midpoint is a point that divides or bisects a segment into two equal segments. If M is a midpoint, then AM = MC. p. 34

Definition segment bisector

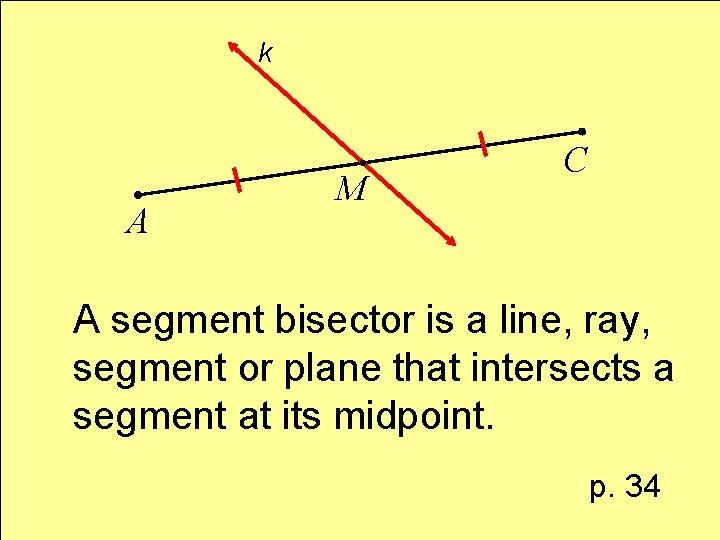
k A M C A segment bisector is a line, ray, segment or plane that intersects a segment at its midpoint. p. 34

Definition angle bisector

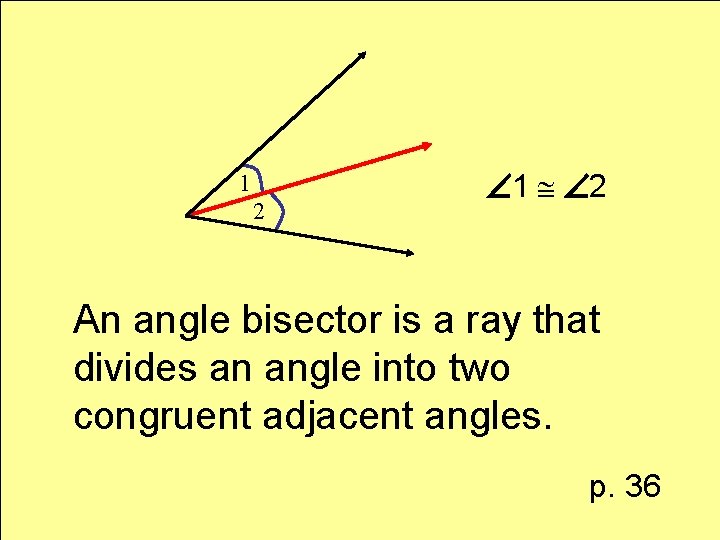
1 2 1 2 An angle bisector is a ray that divides an angle into two congruent adjacent angles. p. 36

Theorem Midpoint Formula

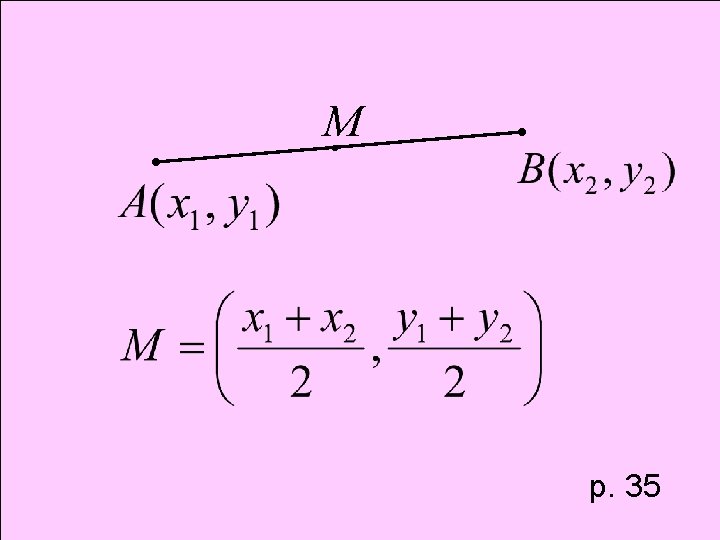
M p. 35

Definition complementary angles

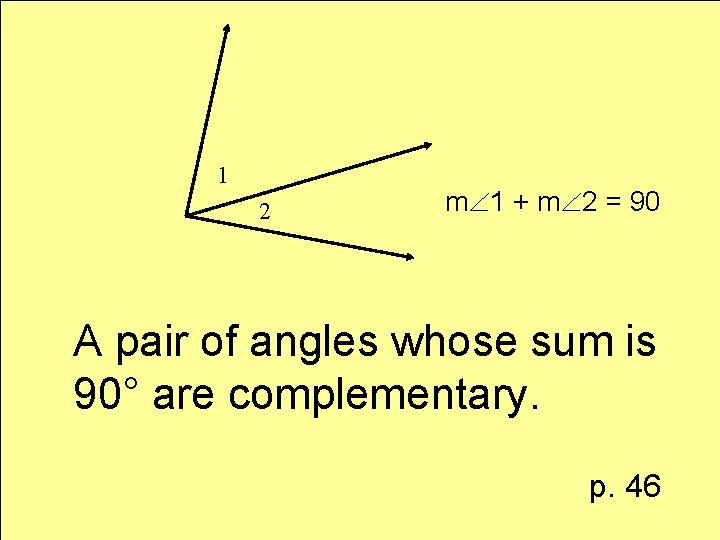
1 2 m 1 + m 2 = 90 A pair of angles whose sum is 90° are complementary. p. 46

Definition supplementary angles

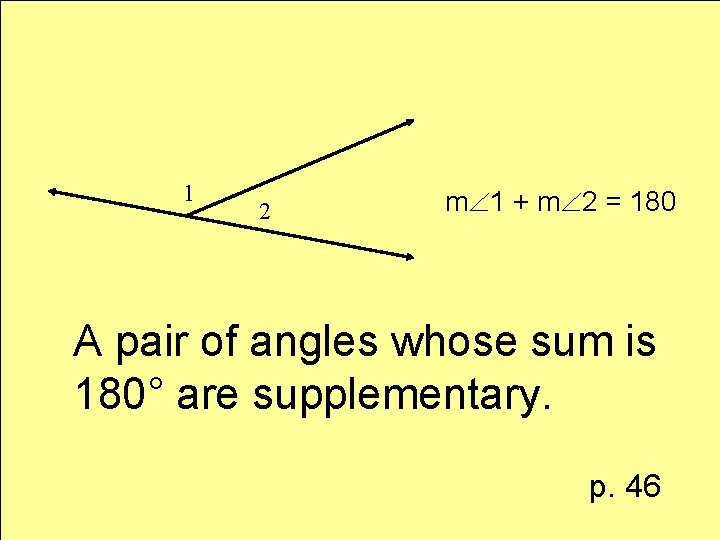
1 2 m 1 + m 2 = 180 A pair of angles whose sum is 180° are supplementary. p. 46

Definition right angle

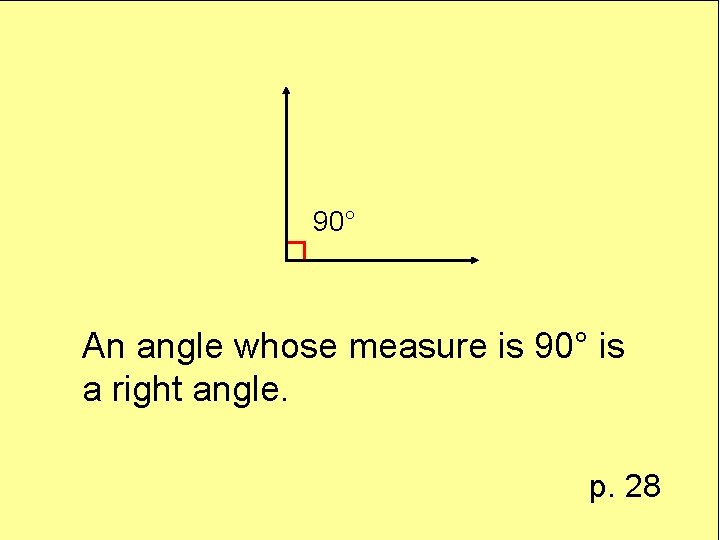
90° An angle whose measure is 90° is a right angle. p. 28

Definition perpendicular lines

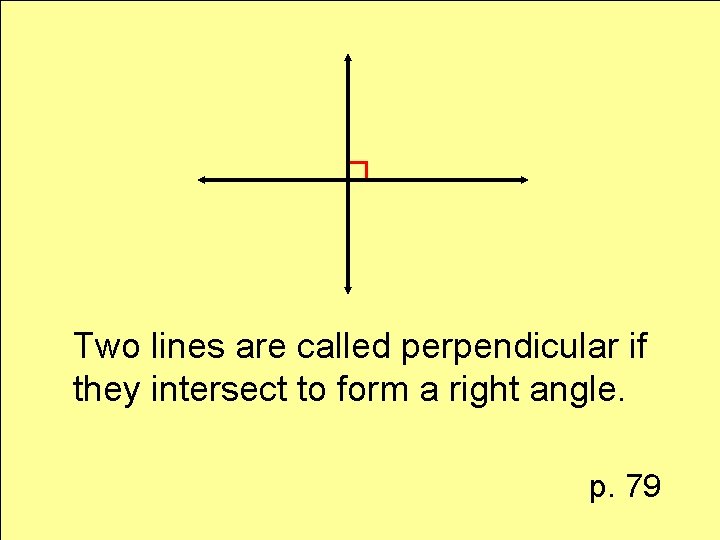
Two lines are called perpendicular if they intersect to form a right angle. p. 79

Property Reflexive

B A D C For any real number, a = a. p. 96

Property Transitive

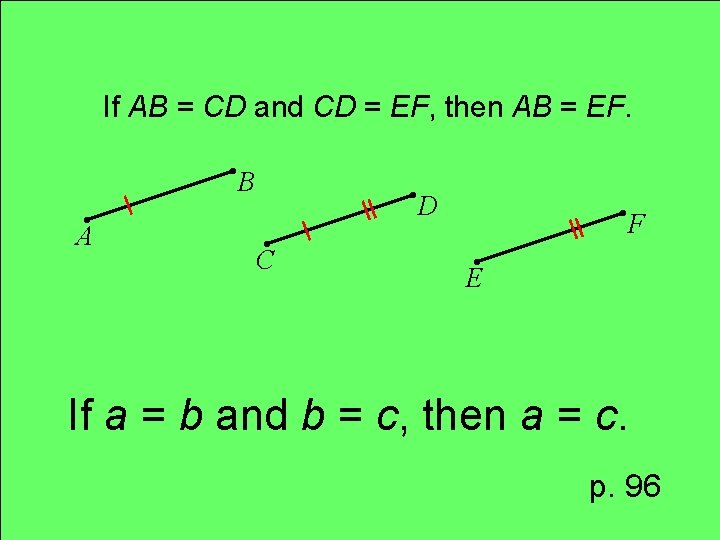
If AB = CD and CD = EF, then AB = EF. . A . B. C . D. . F E If a = b and b = c, then a = c. p. 96

Property Addition Property of Equality

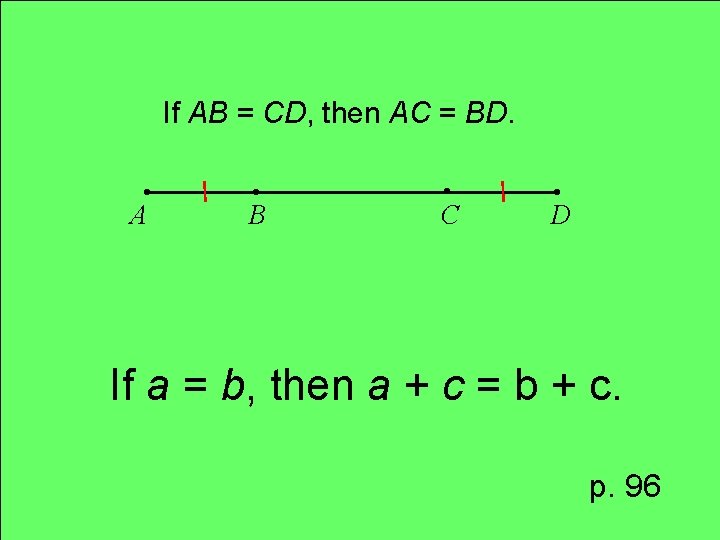
If AB = CD, then AC = BD. . A . B . C . D If a = b, then a + c = b + c. p. 96

Property Subtraction Property of Equality

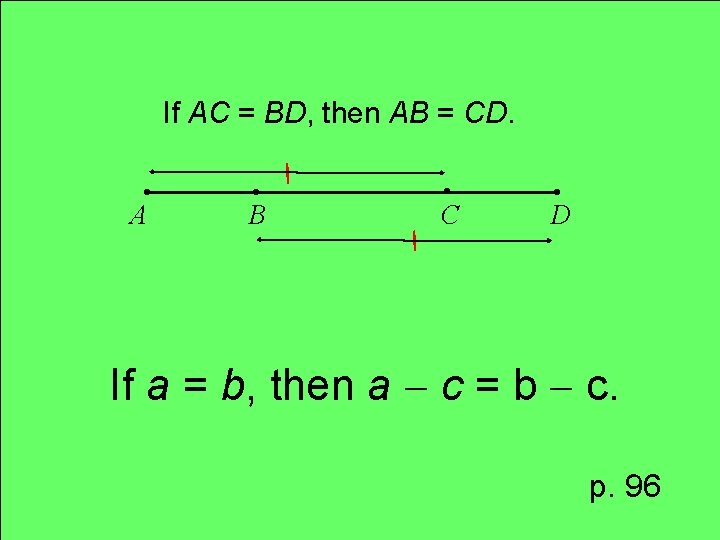
If AC = BD, then AB = CD. . A . B . C . D If a = b, then a c = b c. p. 96

Property Substitution

Example: If AB = 5 + x and x = 3, then AB = 8. If a = b, then a can be substituted for b in any equation or expression. p. 96

Theorem Right Angle Congruence Theorem

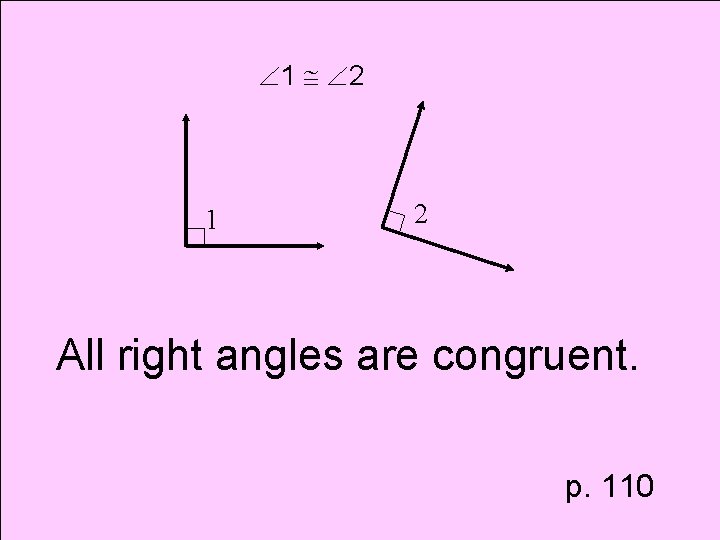
1 2 1 2 All right angles are congruent. p. 110

Theorem Congruent Supplements Theorem

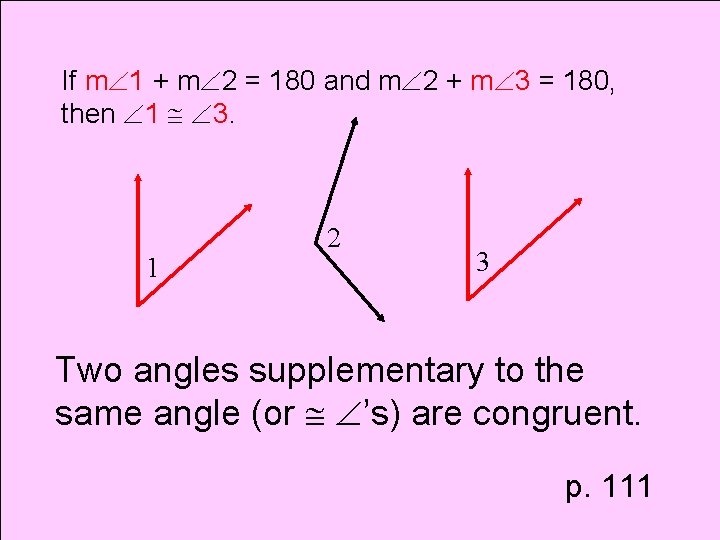
If m 1 + m 2 = 180 and m 2 + m 3 = 180, then 1 3. 1 2 3 Two angles supplementary to the same angle (or ’s) are congruent. p. 111

Theorem Congruent Complements Theorem

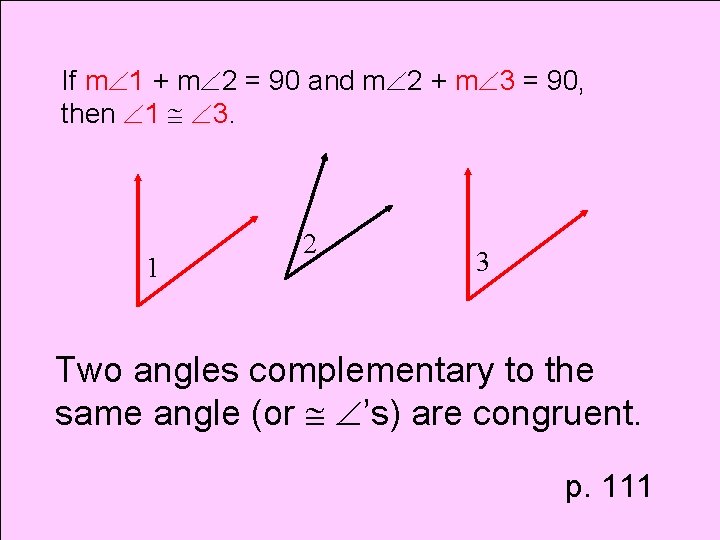
If m 1 + m 2 = 90 and m 2 + m 3 = 90, then 1 3. 1 2 3 Two angles complementary to the same angle (or ’s) are congruent. p. 111

Postulate Linear Pair Postulate

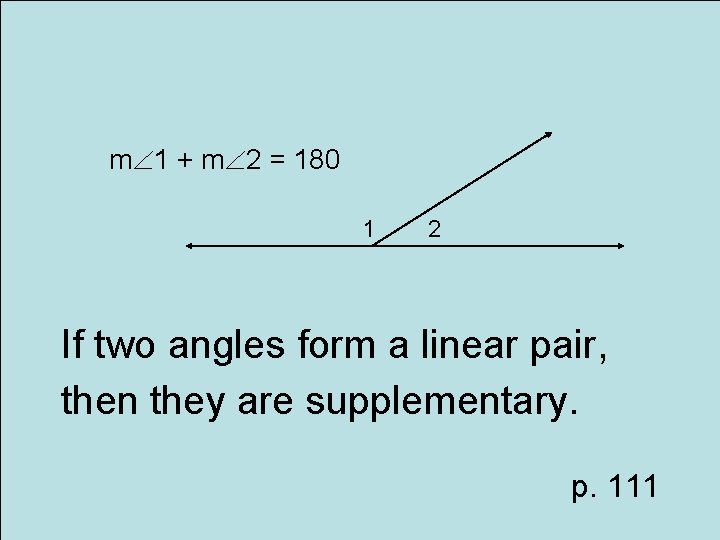
m 1 + m 2 = 180 1 2 If two angles form a linear pair, then they are supplementary. p. 111

Theorem Vertical Angles Theorem

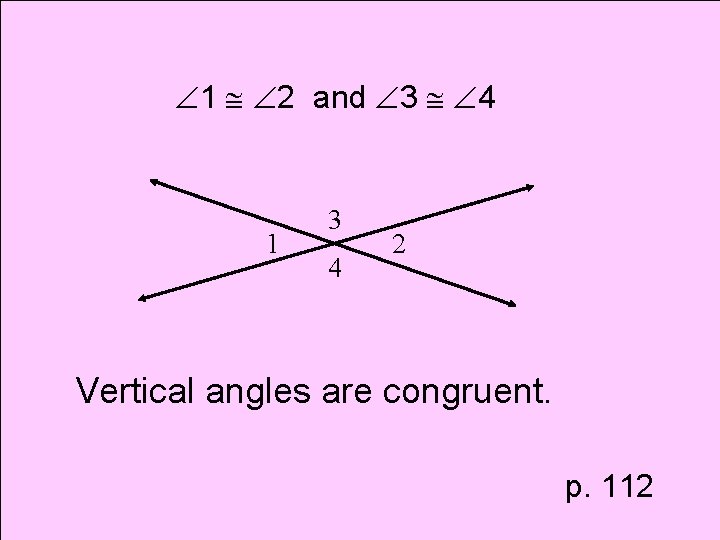
1 2 and 3 4 1 3 4 2 Vertical angles are congruent. p. 112

Theorem Linear Pair of s

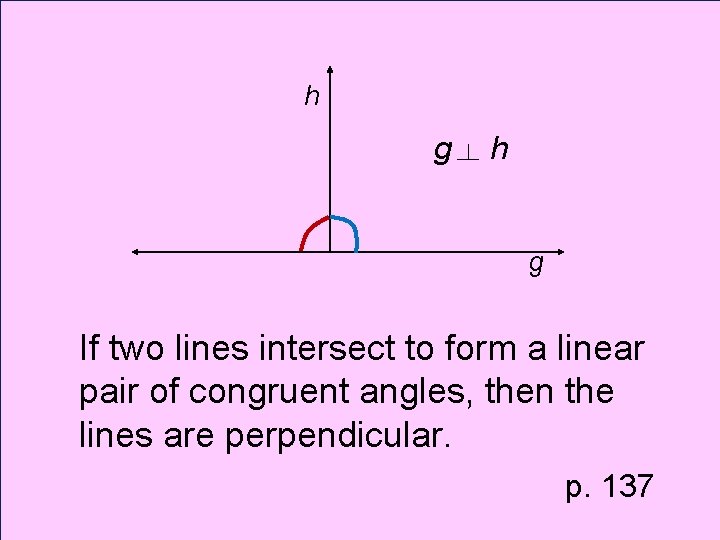
h g If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular. p. 137

Postulate Corresponding Angles Postulate

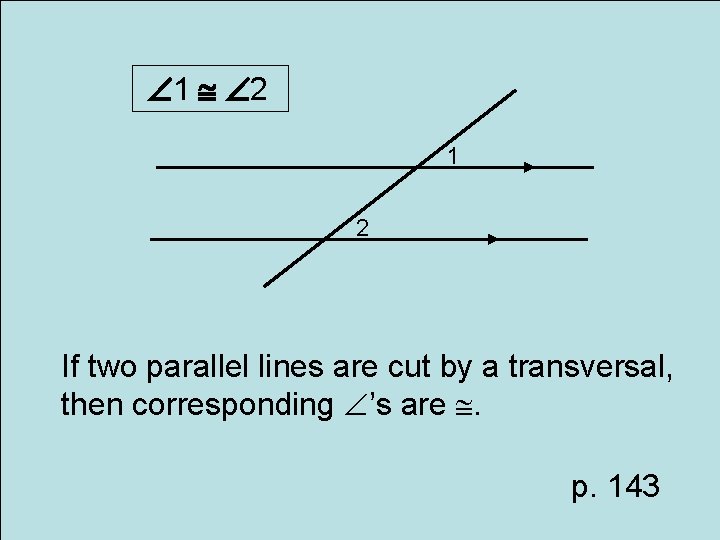
1 2 1 2 If two parallel lines are cut by a transversal, then corresponding ’s are . p. 143

Theorem Alternate Interior Angles Theorem

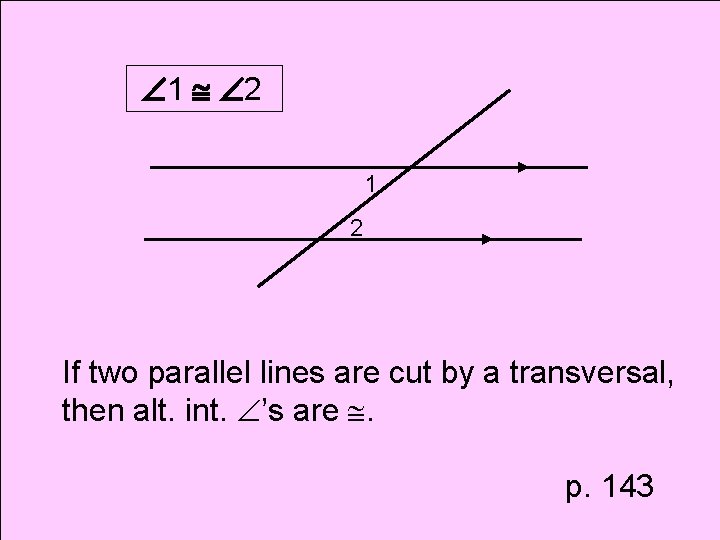
1 2 1 2 If two parallel lines are cut by a transversal, then alt. int. ’s are . p. 143

Theorem Alternate Exterior Angles Theorem

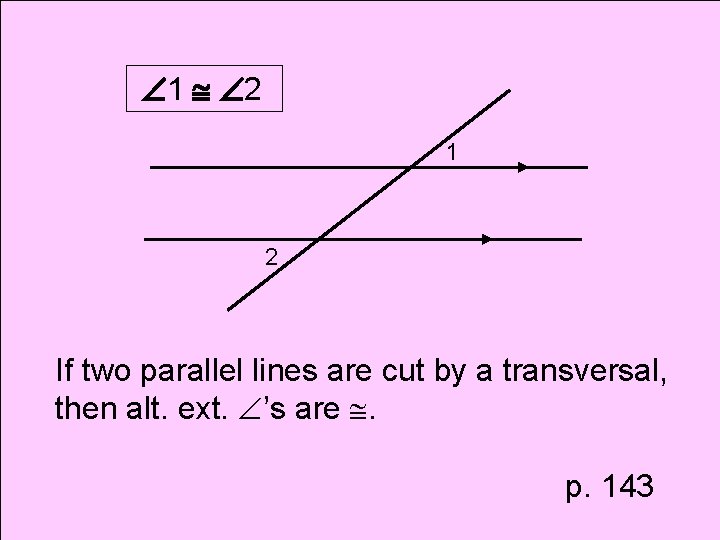
1 2 1 2 If two parallel lines are cut by a transversal, then alt. ext. ’s are . p. 143

Theorem Consecutive Interior Angles Theorem

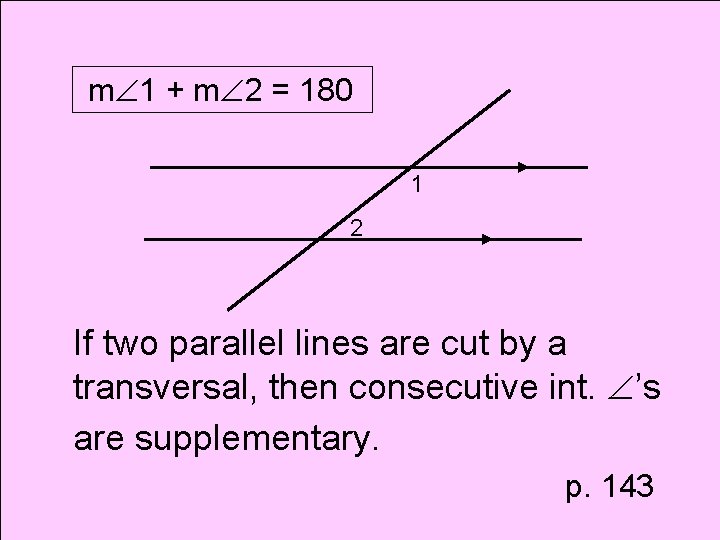
m 1 + m 2 = 180 1 2 If two parallel lines are cut by a transversal, then consecutive int. ’s are supplementary. p. 143

Theorem Perpendicular Transversal Theorem

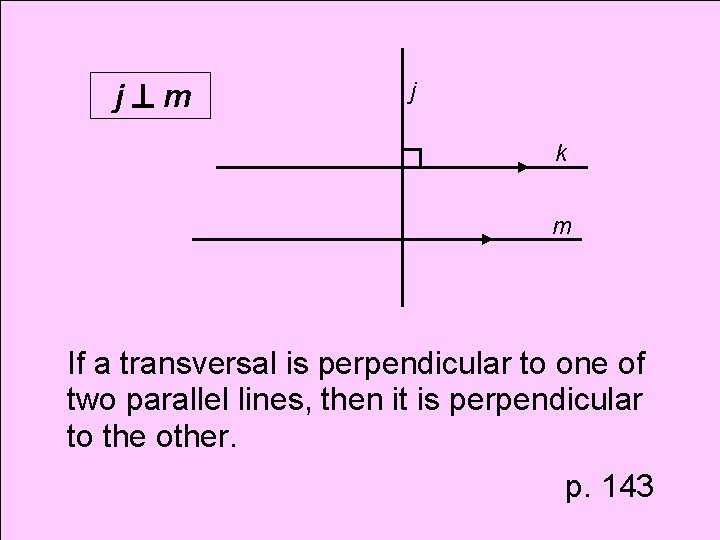
j m j k m If a transversal is perpendicular to one of two parallel lines, then it is perpendicular to the other. p. 143

Theorem Two Lines Perpendicular to Same Line

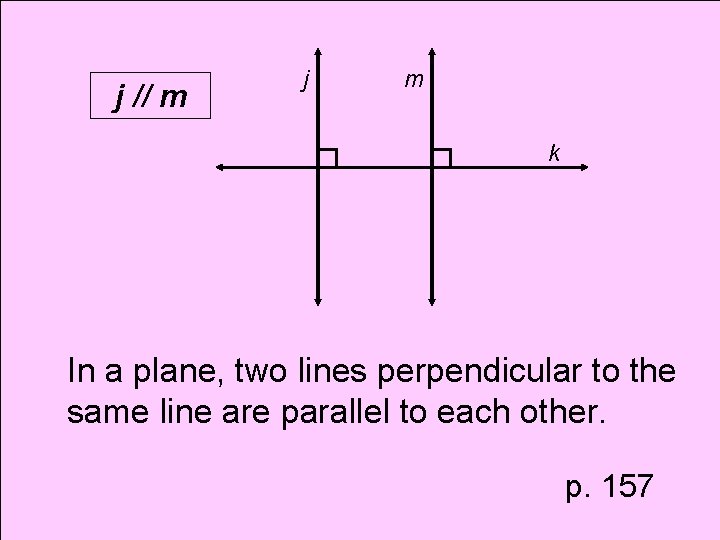
j // m j m k In a plane, two lines perpendicular to the same line are parallel to each other. p. 157

Theorem Two Lines Parallel to the Same Line

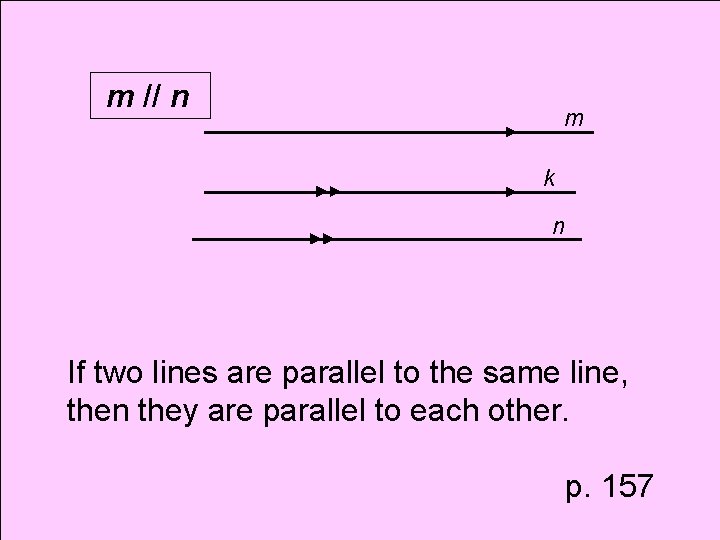
m // n m k n If two lines are parallel to the same line, then they are parallel to each other. p. 157

Theorem Triangle Sum Theorem

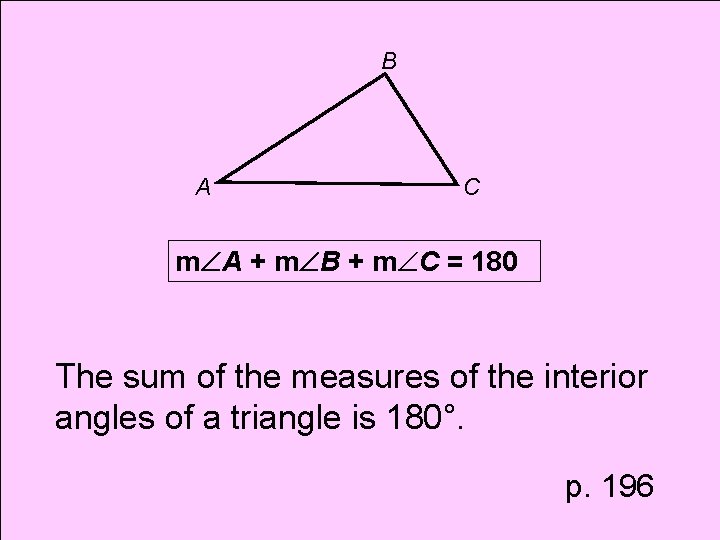
B A C m A + m B + m C = 180 The sum of the measures of the interior angles of a triangle is 180°. p. 196

Theorem Exterior Angle Theorem

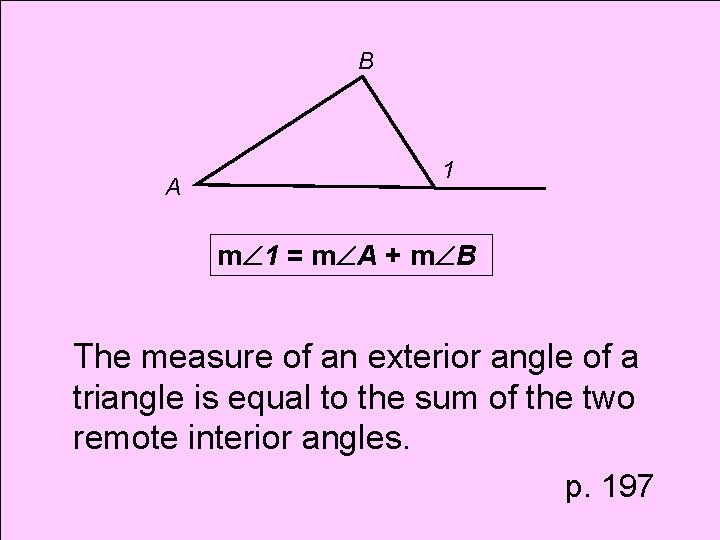
B A 1 m 1 = m A + m B The measure of an exterior angle of a triangle is equal to the sum of the two remote interior angles. p. 197

Theorem Third Angles Theorem

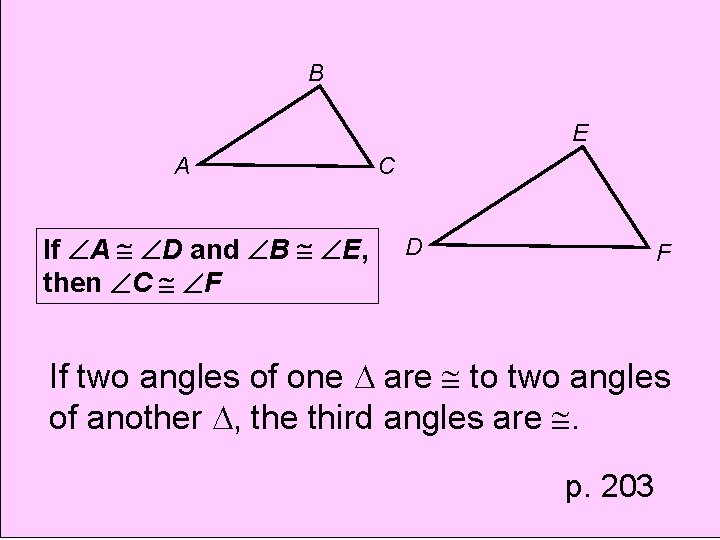
B E A If A D and B E, then C F C D F If two angles of one are to two angles of another , the third angles are . p. 203

Postulate SSS Side-Side Congruence

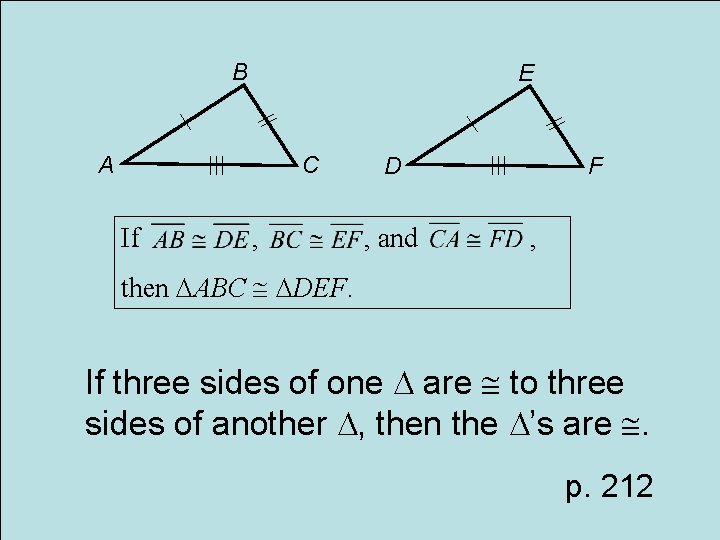
B E A C If , D , and F , then ABC DEF. If three sides of one are to three sides of another , then the ’s are . p. 212

Postulate SAS Side-Angle-Side Congruence

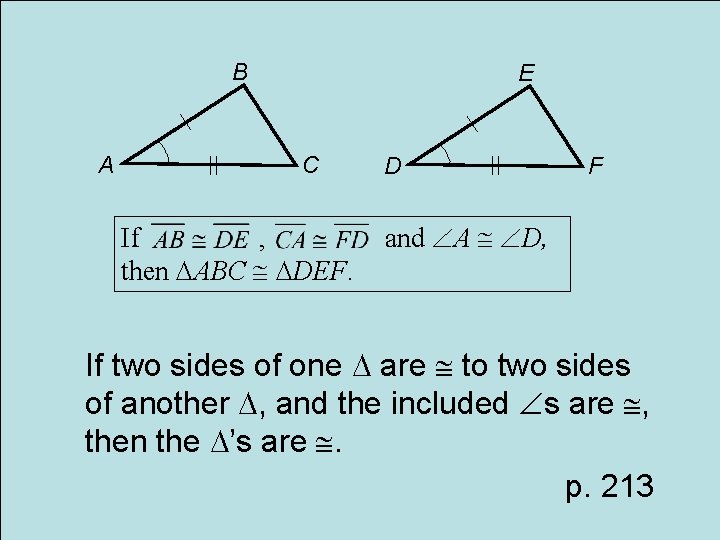
B A E C If , then ABC DEF. D F and A D, If two sides of one are to two sides of another , and the included s are , then the ’s are . p. 213

Theorem Perpendicular/Right Theorem (Meyers Theorem)

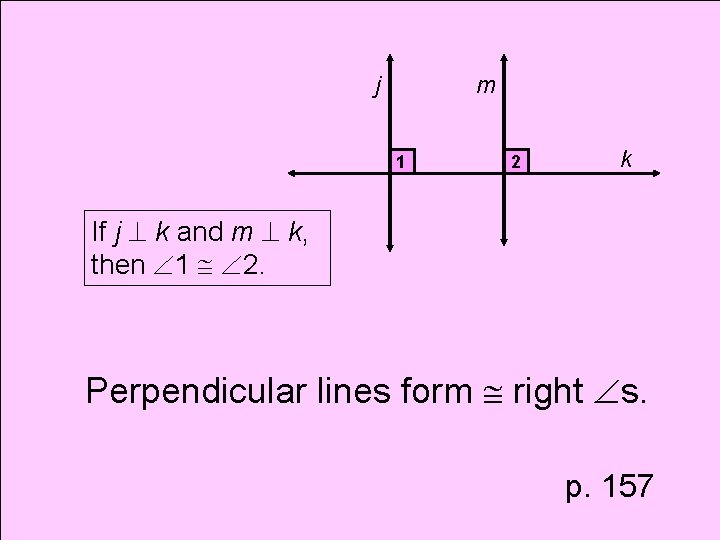
j m 1 2 k If j k and m k, then 1 2. Perpendicular lines form right s. p. 157

Postulate ASA Angle-Side-Angle Congruence

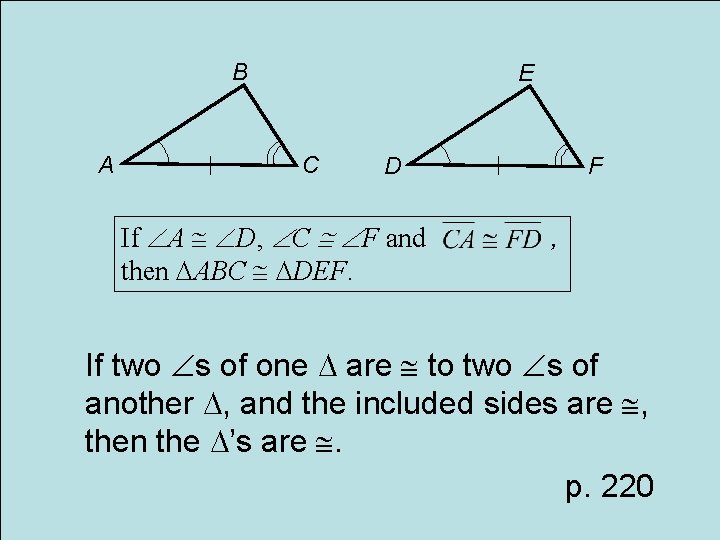
B A E C D If A D, C F and then ABC DEF. F , If two s of one are to two s of another , and the included sides are , then the ’s are . p. 220

Postulate AAS Angle-Side Congruence

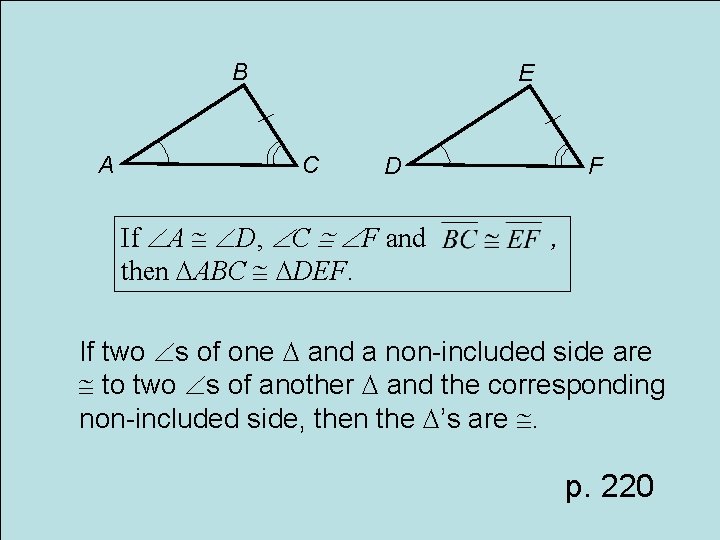
B A E C D If A D, C F and then ABC DEF. F , If two s of one and a non-included side are to two s of another and the corresponding non-included side, then the ’s are . p. 220

Theorem Base Angles Theorem

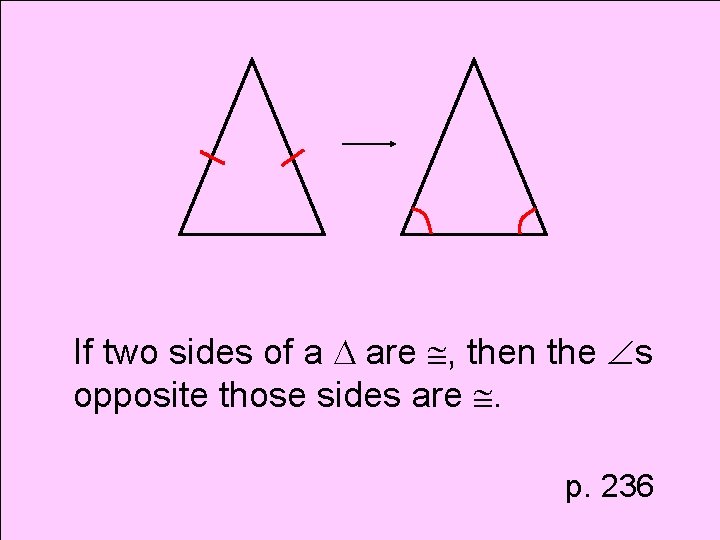
If two sides of a are , then the s opposite those sides are . p. 236

Theorem Base Angles Converse Theorem

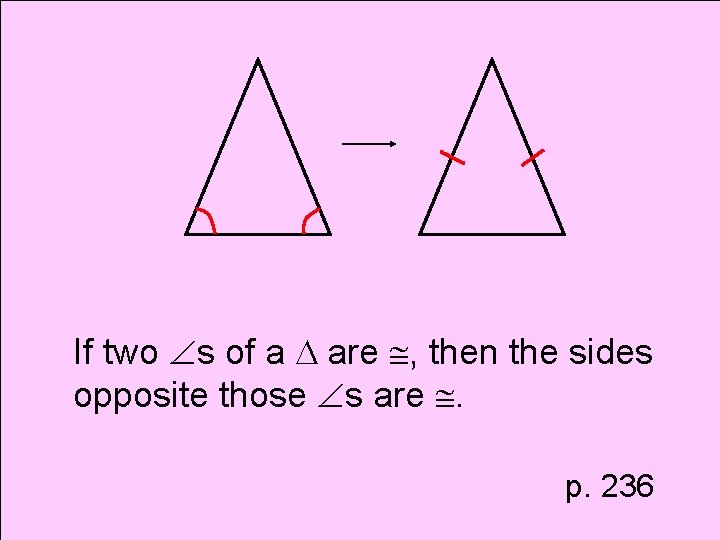
If two s of a are , then the sides opposite those s are . p. 236

Theorem Hypotenuse-Leg Theorem H-L

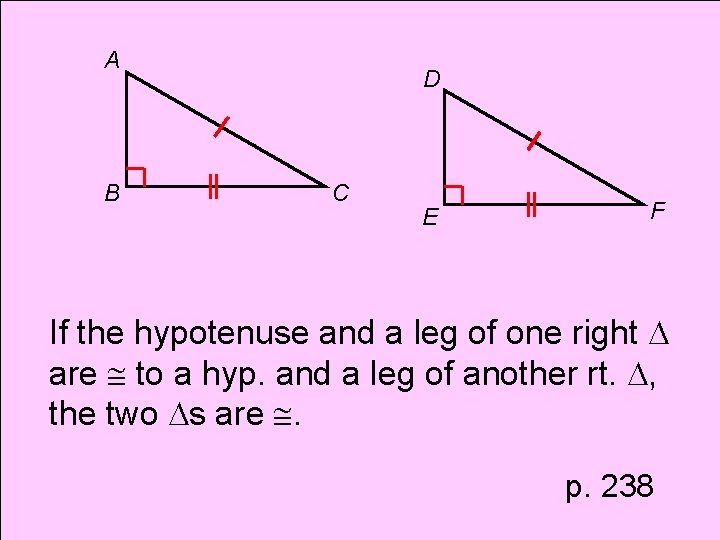
A B D C E F If the hypotenuse and a leg of one right are to a hyp. and a leg of another rt. , the two s are . p. 238

Theorem Perpendicular Bisector Theorem

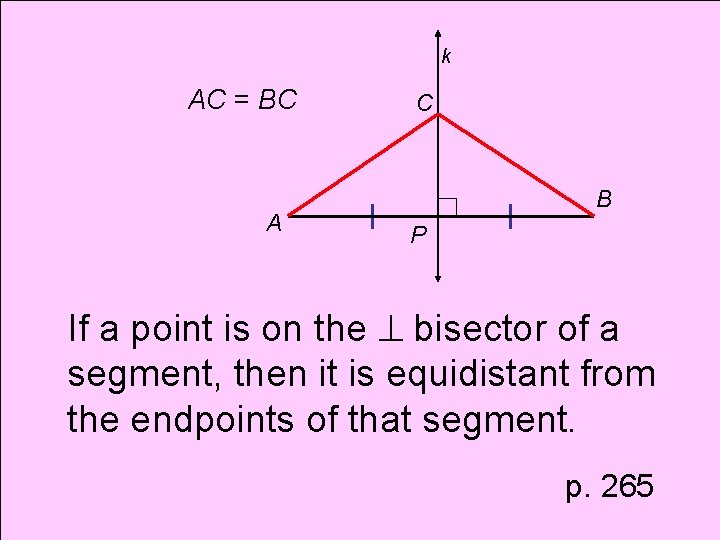
k AC = BC A C B P If a point is on the bisector of a segment, then it is equidistant from the endpoints of that segment. p. 265

Theorem Angle Bisector Theorem

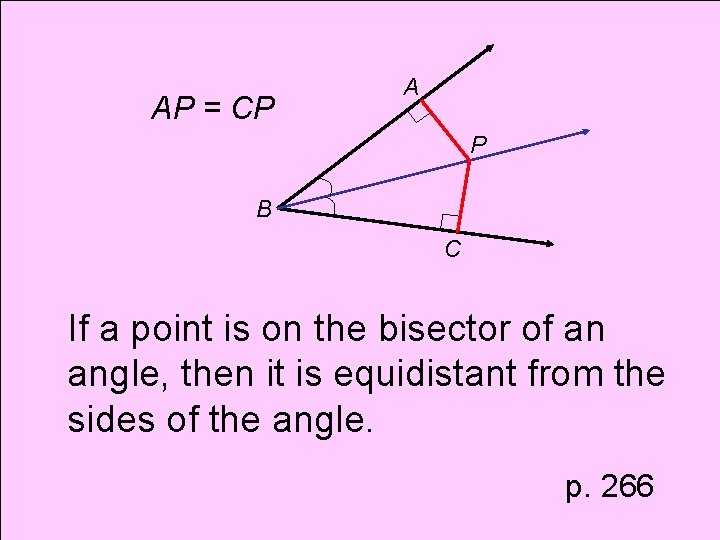
AP = CP A P B C If a point is on the bisector of an angle, then it is equidistant from the sides of the angle. p. 266

Theorem Circumcenter

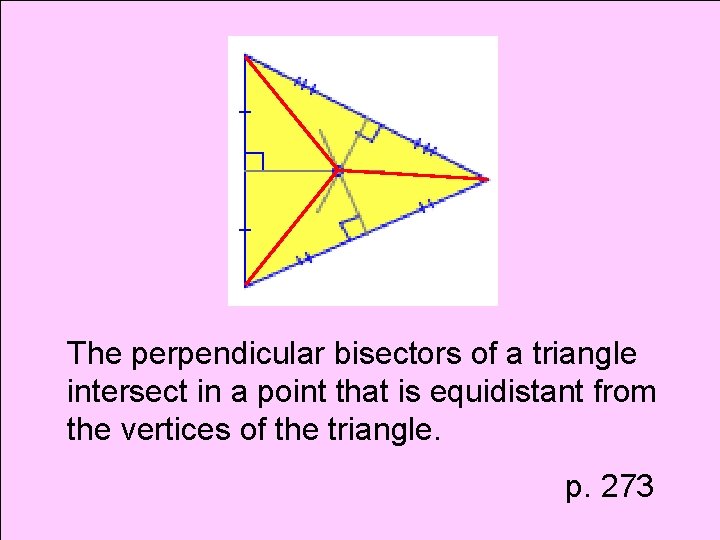
The perpendicular bisectors of a triangle intersect in a point that is equidistant from the vertices of the triangle. p. 273

Theorem Incenter

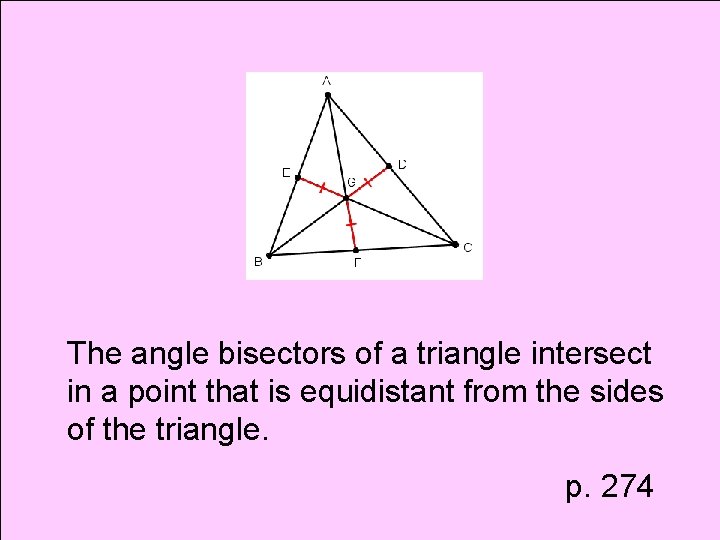
The angle bisectors of a triangle intersect in a point that is equidistant from the sides of the triangle. p. 274

Theorem Centroid

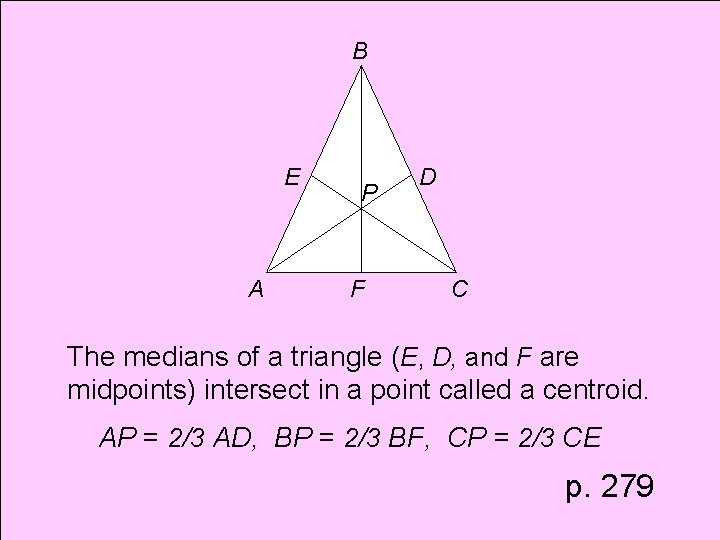
B E A P F D C The medians of a triangle (E, D, and F are midpoints) intersect in a point called a centroid. AP = 2/3 AD, BP = 2/3 BF, CP = 2/3 CE p. 279

Theorem Orthocenter

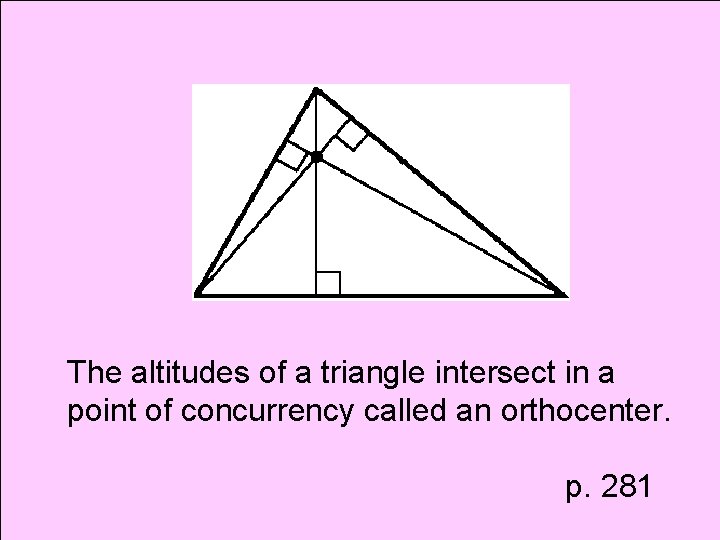
The altitudes of a triangle intersect in a point of concurrency called an orthocenter. p. 281