Thema von Sarah Otto berblick 1 Parameterformen 1

Thema von: Sarah Otto

Überblick 1. Parameterformen 1. 1 Punkt - Richtungsform 1. 2 Drei - Punkte – Form 2. Die Koordinatenformen 2. 1 Achsenabschnittsform 2. 2 Normalenform 2. 3 Hessesche Normalform 3. Umwandlung 4. Lagebeziehungen / Schnitte 5. Schnittwinkel 1/22

1. Parameterformen Die beiden Parameterformen: 1. 1 Punkt-Richtungs-Form 1. 2 Drei-Punkte-Form 2/22

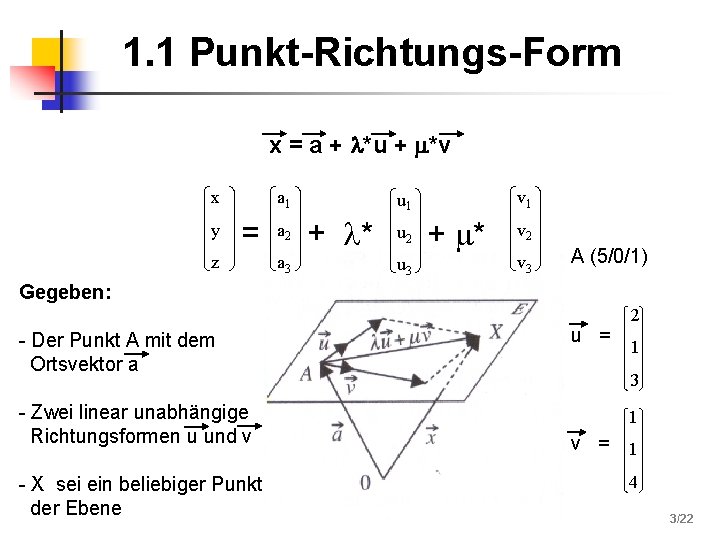
1. 1 Punkt-Richtungs-Form x = a + *u + *v x y a 1 = z a 2 a 3 v 1 u 1 + * u 2 u 3 + * v 2 v 3 A (5/0/1) Gegeben: - Der Punkt A mit dem Ortsvektor a - Zwei linear unabhängige Richtungsformen u und v - X sei ein beliebiger Punkt der Ebene u = 2 1 3 1 v = 1 4 3/22

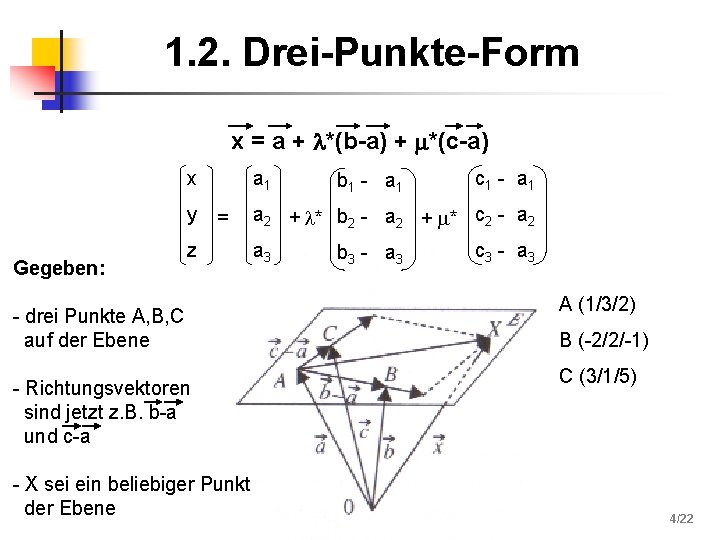
1. 2. Drei-Punkte-Form x = a + *(b-a) + *(c-a) x y Gegeben: a 1 = z - drei Punkte A, B, C auf der Ebene - Richtungsvektoren sind jetzt z. B. b-a und c-a - X sei ein beliebiger Punkt der Ebene b 1 - a 1 c 1 - a 1 a 2 + * b 2 - a 2 + * c 2 - a 2 a 3 b 3 - a 3 c 3 - a 3 A (1/3/2) B (-2/2/-1) C (3/1/5) 4/22

2. Koordinatenformen Die Koordinatenformen 2. 1 Achsenabschnittsform 2. 2 Normalenform 2. 3 Hessesche Normalenform 5/22

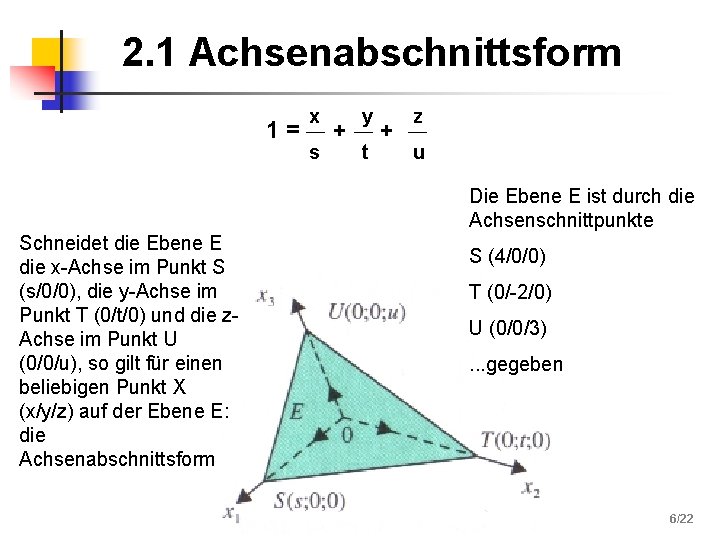
2. 1 Achsenabschnittsform 1= x s + y t + z u Die Ebene E ist durch die Achsenschnittpunkte Schneidet die Ebene E die x-Achse im Punkt S (s/0/0), die y-Achse im Punkt T (0/t/0) und die z. Achse im Punkt U (0/0/u), so gilt für einen beliebigen Punkt X (x/y/z) auf der Ebene E: die Achsenabschnittsform S (4/0/0) T (0/-2/0) U (0/0/3). . . gegeben 6/22

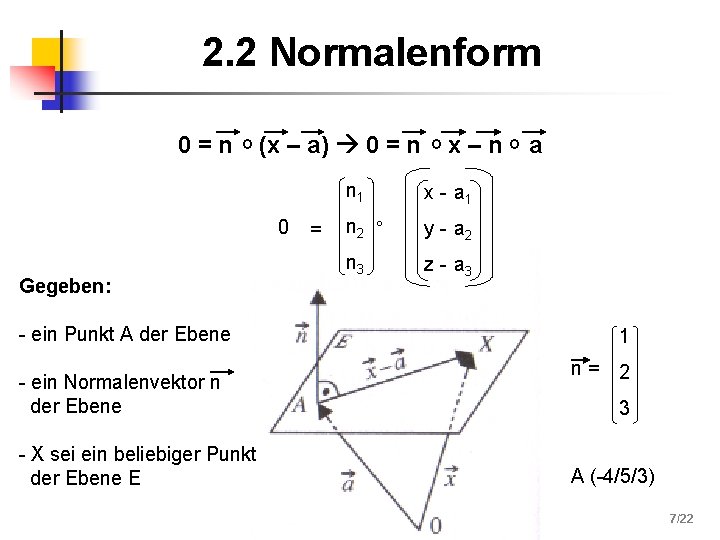
2. 2 Normalenform 0 = n ° (x – a) 0 = n ° x – n ° a 0 Gegeben: - ein Punkt A der Ebene - ein Normalenvektor n der Ebene - X sei ein beliebiger Punkt der Ebene E = n 1 x - a 1 n 2 ° y - a 2 n 3 z - a 3 1 n= 2 3 A (-4/5/3) 7/22

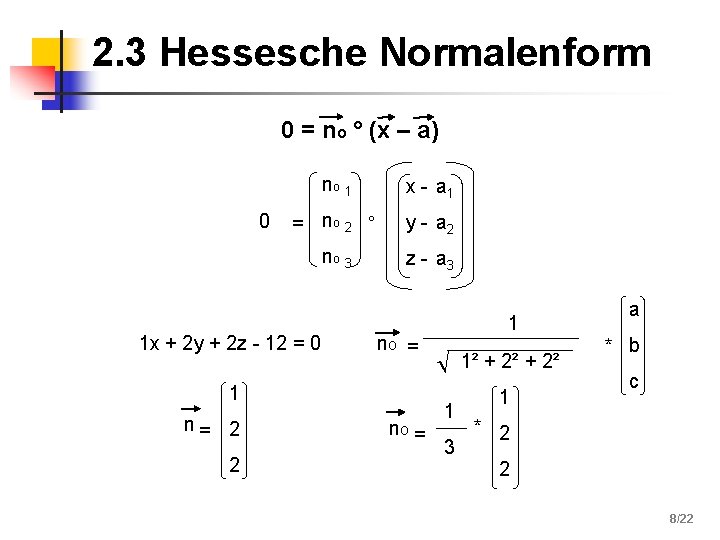
2. 3 Hessesche Normalenform 0 = no ° (x – a) 0 no 1 x - a 1 = no 2 ° y - a 2 no 3 z - a 3 1 x + 2 y + 2 z - 12 = 0 no = 1 n= 2 2 no = 1 1² + 2² 1 3 1 a * b c * 2 2 8/22

3. Umwandlung Umwandeln in andere Darstellungsformen: 3. 1 Umwandlung von der Parameterform in Koordinatenform und – Normalenform 3. 2 Umwandlung von der Koordinatenform in die - Normalenform - Hessesche Normalenform und - Parameterform 9/22

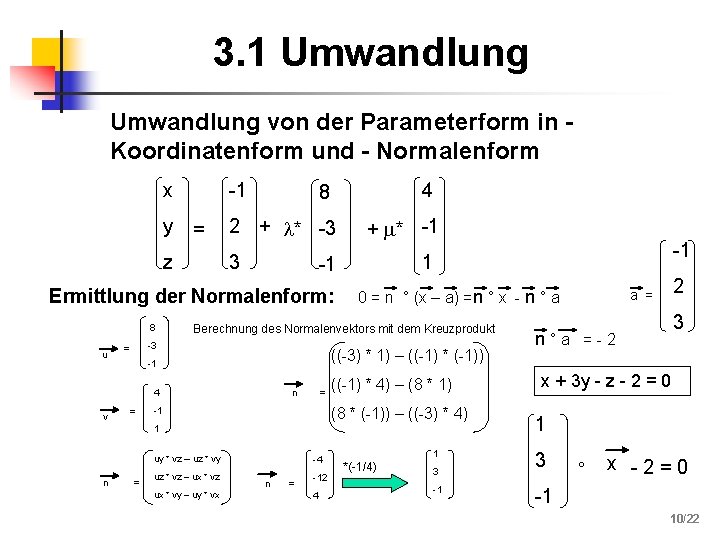
3. 1 Umwandlung von der Parameterform in Koordinatenform und - Normalenform x y -1 = z 4 8 2 + * -3 3 u ((-3) * 1) – ((-1) * (-1)) -1 n 4 v = 0 = n ° (x – a) =n ° x - n ° a Berechnung des Normalenvektors mit dem Kreuzprodukt -3 = = ((-1) * 4) – (8 * 1) (8 * (-1)) – ((-3) * 4) -1 1 uy * vz – uz * vy n = uz * vz – ux * vz ux * vy – uy * vx -4 n = -12 4 -1 1 -1 Ermittlung der Normalenform: 8 + * -1 1 *(-1/4) 3 -1 2 a = 3 n°a =-2 x + 3 y - z - 2 = 0 1 3 ° x -2=0 -1 10/22

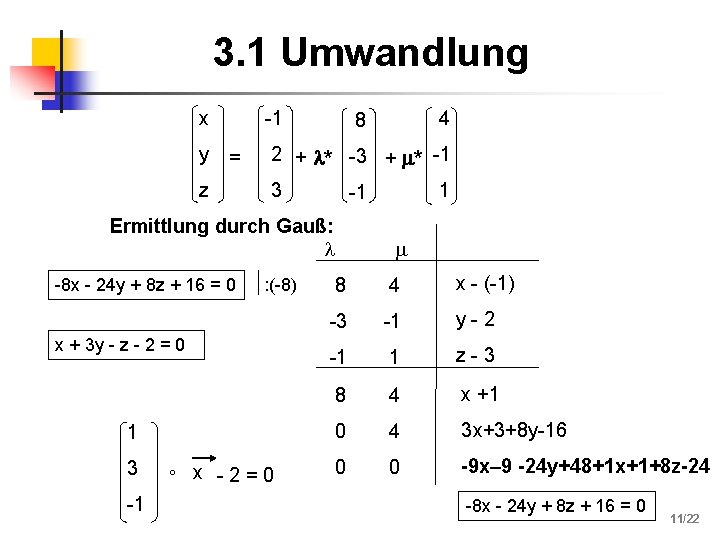
3. 1 Umwandlung x y -1 = z 2 + * -3 + * -1 3 : (-8) x + 3 y - z - 2 = 0 1 3 -1 ° x -2=0 1 -1 Ermittlung durch Gauß: -8 x - 24 y + 8 z + 16 = 0 4 8 8 4 x - (-1) -3 -1 y-2 -1 1 z-3 8 4 x +1 0 4 3 x+3+8 y-16 0 0 -9 x– 9 -24 y+48+1 x+1+8 z-24 -8 x - 24 y + 8 z + 16 = 0 11/22

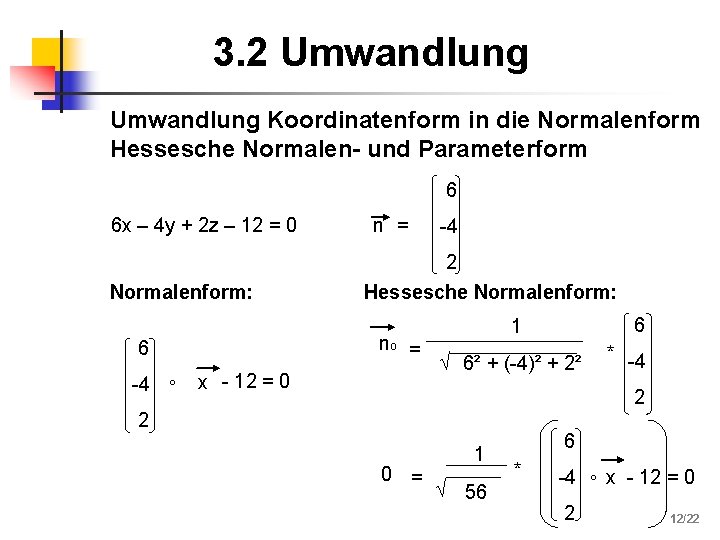
3. 2 Umwandlung Koordinatenform in die Normalenform Hessesche Normalen- und Parameterform 6 6 x – 4 y + 2 z – 12 = 0 Normalenform: -4 2 Hessesche Normalenform: no = 6 -4 ° n = x - 12 = 0 6 1 6² + (-4)² + 2² * -4 2 2 0 = 1 56 6 * -4 ° x - 12 = 0 2 12/22

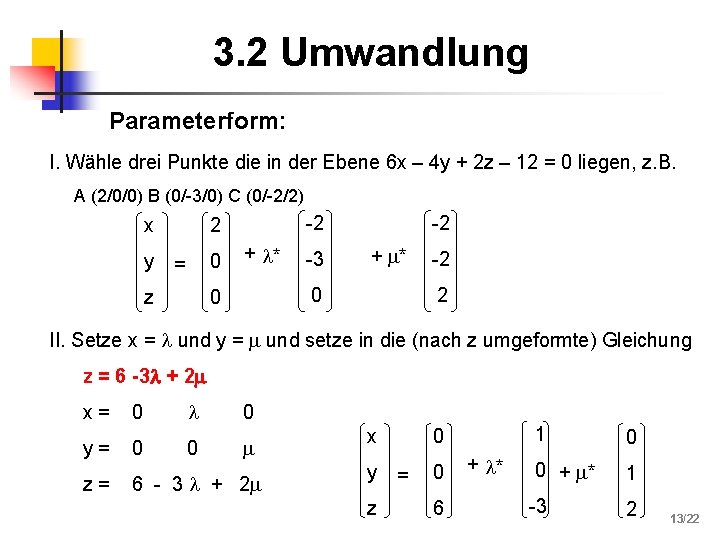
3. 2 Umwandlung Parameterform: I. Wähle drei Punkte die in der Ebene 6 x – 4 y + 2 z – 12 = 0 liegen, z. B. A (2/0/0) B (0/-3/0) C (0/-2/2) x y -2 2 0 = z + * -3 -2 + * 0 0 -2 2 II. Setze x = und y = und setze in die (nach z umgeformte) Gleichung z = 6 -3 + 2 x= 0 0 y= 0 0 z= 6 - 3 + 2 x y z 0 = 0 6 + * 1 0 0 + * 1 -3 2 13/22

4. Lagebeziehungen: 4. 1 Lage von Punkt und Ebene zueinander 4. 2 Lage von Gerade und Ebene zueinander 14/22

4. 1 Punkt - Ebene P (5/-3/3) II. Ermitteln der Parameter und durch Gauß: 3 -1 -3 1, 5 + * -1, 5 + * 3 0 2 1 -1 -3 2 -1, 5 3 -4, 5 3 -1 -3 2 1 3 -3 = 1, 5 + * -1, 5 + * 3 -1 -3 2 0 7, 5 -7, 5 3 0 2 1 0 -5 7 x y = z 5 5 = 3 - - 3 = -3 - 2 -5 = 7 = - 1, 4 -3 = 1, 5 – 1, 5 + 3 7, 5 = -7, 5 = -1 3 = 0 + 2 + Daraus folgt: P E 15/22

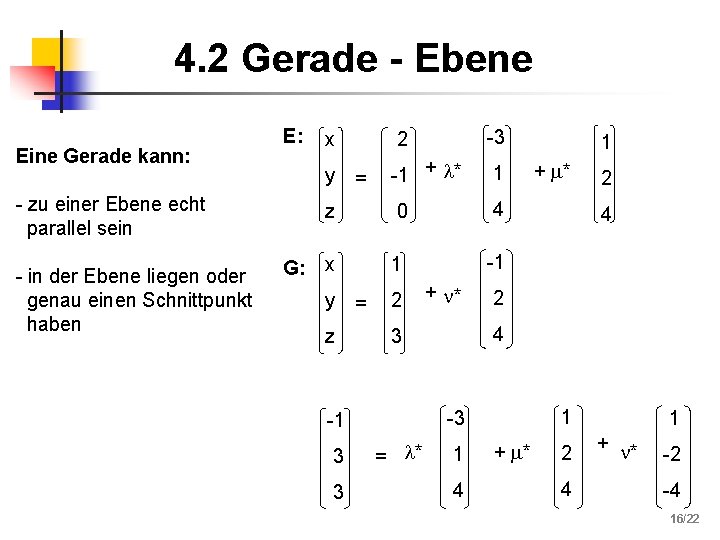
4. 2 Gerade - Ebene Eine Gerade kann: - zu einer Ebene echt parallel sein - in der Ebene liegen oder genau einen Schnittpunkt haben E: 2 -3 -1 + * 1 z 0 4 G: x 1 -1 x y y z = = 2 3 2 4 2 1 -3 = * + * 4 3 -1 3 + * 1 1 4 + * 2 4 1 + * -2 -4 16/22

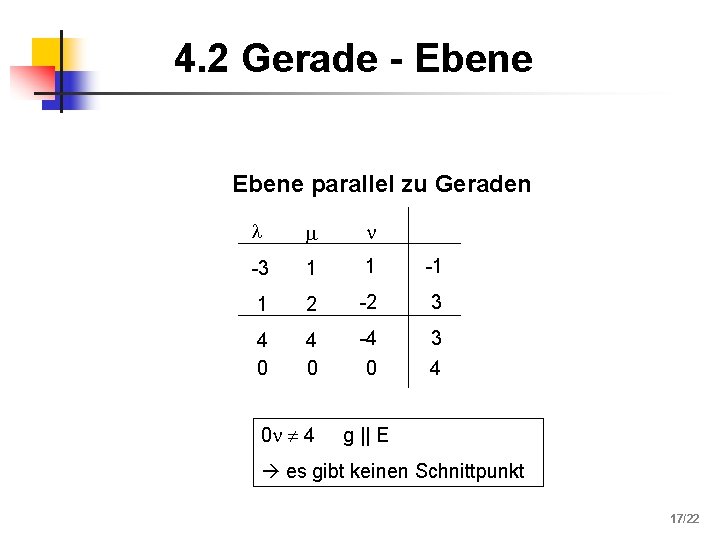
4. 2 Gerade - Ebene parallel zu Geraden -3 1 1 -1 1 2 -2 3 4 0 -4 3 0 4 0 4 g || E es gibt keinen Schnittpunkt 17/22

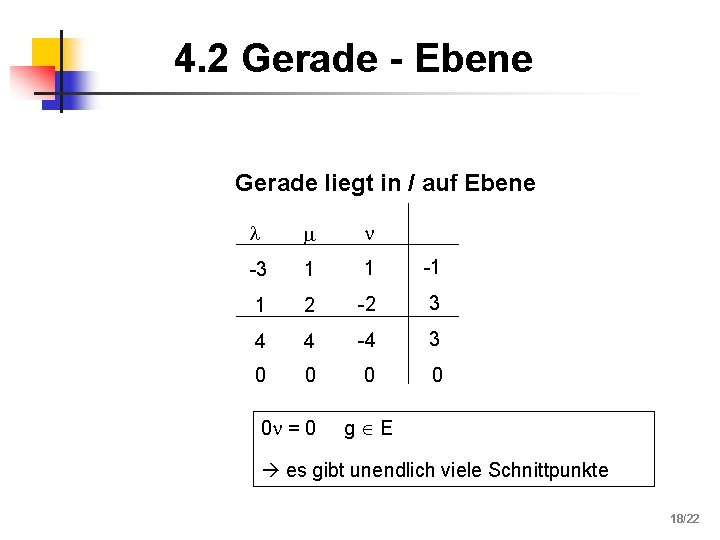
4. 2 Gerade - Ebene Gerade liegt in / auf Ebene -3 1 1 -1 1 2 -2 3 4 4 -4 3 0 0 0 = 0 g E es gibt unendlich viele Schnittpunkte 18/22

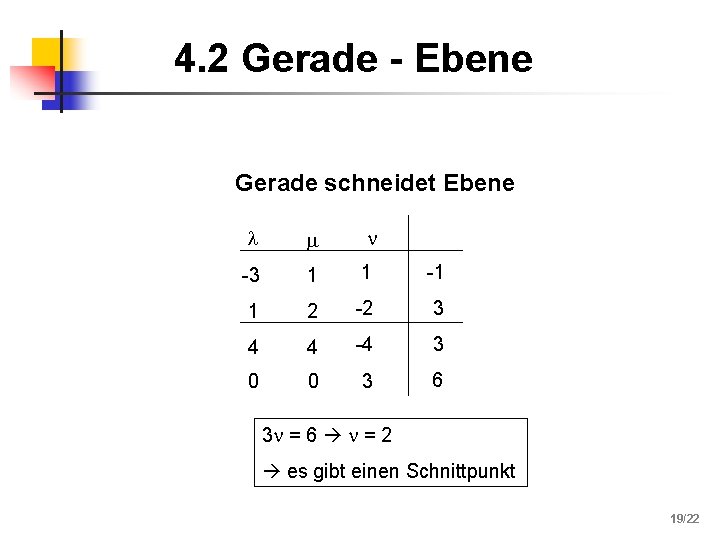
4. 2 Gerade - Ebene Gerade schneidet Ebene -3 1 1 -1 1 2 -2 3 4 4 -4 3 0 0 3 6 3 = 6 = 2 es gibt einen Schnittpunkt 19/22

5. Schnittwinkel bei Ebenen: 5. 1 Schnittwinkel zwischen Gerade und Ebene 5. 2 Schnittwinkel zwischen Ebene und Ebene 20/22

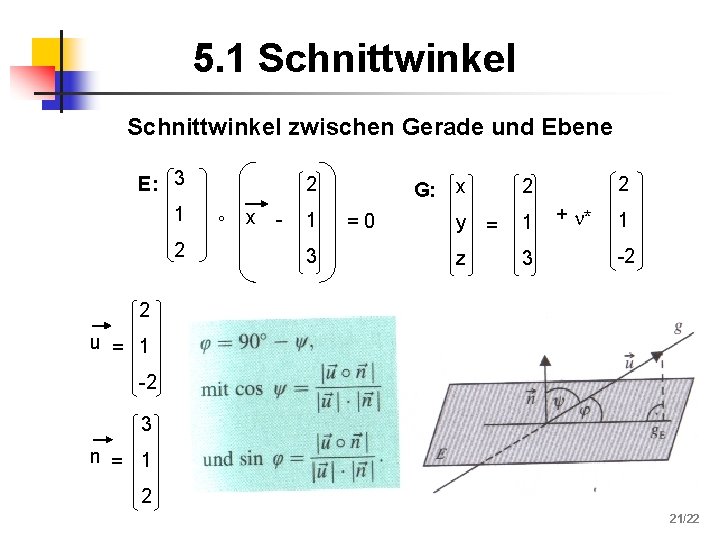
5. 1 Schnittwinkel zwischen Gerade und Ebene E: 3 1 2 2 ° x - 1 3 G: x =0 y z 2 2 = 1 3 + * 1 -2 2 u = 1 -2 3 n = 1 2 21/22

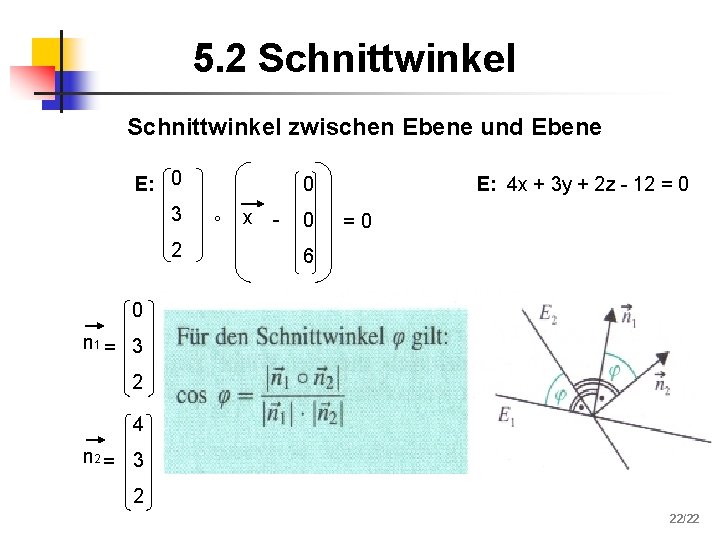
5. 2 Schnittwinkel zwischen Ebene und Ebene E: 0 3 2 0 ° x - 0 E: 4 x + 3 y + 2 z - 12 = 0 =0 6 0 n 1 = 3 2 4 n 2 = 3 2 22/22

Ende Vielen Dank für Ihre Aufmerksamkeit =)