The Webster and Hill Method for Apportionment Both

The Webster and Hill Method for Apportionment Both are like the Jefferson method

Webster • Instead of truncating to find the initial distribution use the rounding method that is most familiar (. 5 and above round up below. 5 round down) • Count up the number of sear distributed and determine how many seat need to be add or taken away.

Webster • If there are 6 different coalitions that control the following populations how would Webster distribute 35 seats. • A 979 • B 868 • C 590 • D 449 • E 356 • F 258

Webster initial distribution
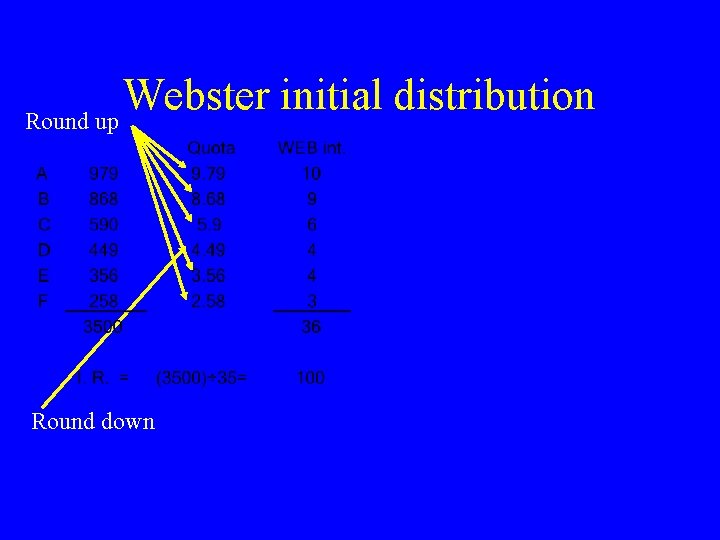
Webster initial distribution Round up Round down

Webster initial distribution Round up Round down To lose a seat. Divide by the rounding point below the int. That is. 5 below the int. One to many

Webster initial distribution Round up Round down To lose a seat. Divide by the rounding point below the int. That is. 5 below the int. One to many

Webster initial distribution Round up Round down To lose a seat. Divide by the rounding point below the int. That is. 5 below the int. One to many

Hill • Instead of truncating to find the initial distribution round at the geometry mean ( if quota is 4. 48 then the geometric mean is √(4 x 5)= 4. 4721. Round up to 5) • Count up the number of seats distributed and determine how many seat need to be add or taken away.

Hill • If there are 6 different coalitions that control the following populations how would Hill distribute 35 seats. • A 979 • B 868 • C 590 • D 449 • E 356 • F 258
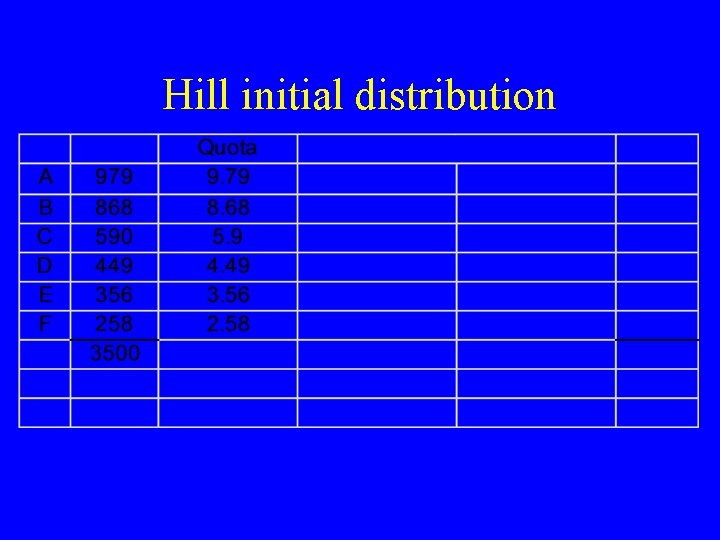
Hill initial distribution

Hill initial distribution Round up because they are greater than the geometric mean
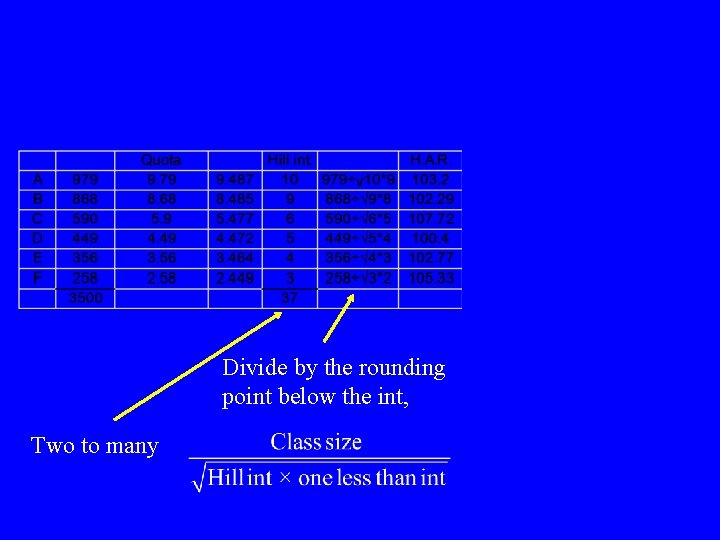
Divide by the rounding point below the int, Two to many
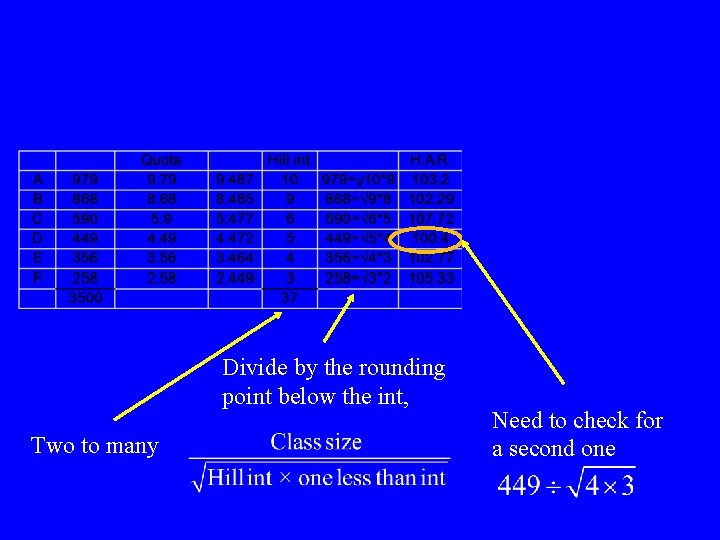
Divide by the rounding point below the int, Two to many Need to check for a second one
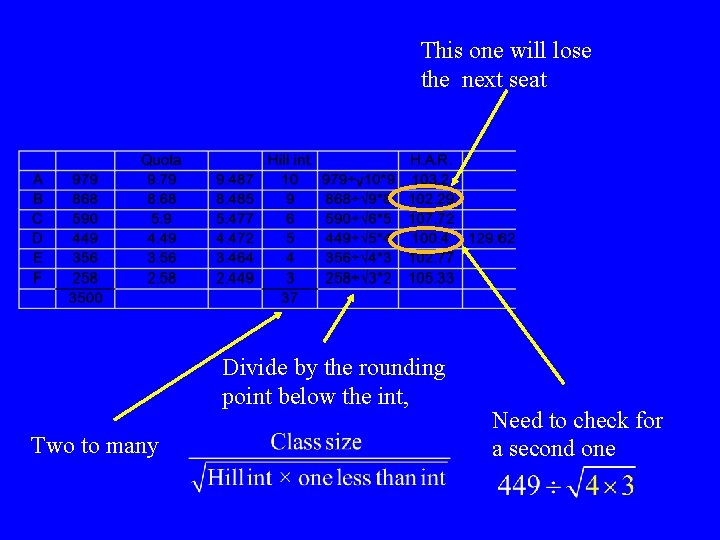
This one will lose the next seat Divide by the rounding point below the int, Two to many Need to check for a second one
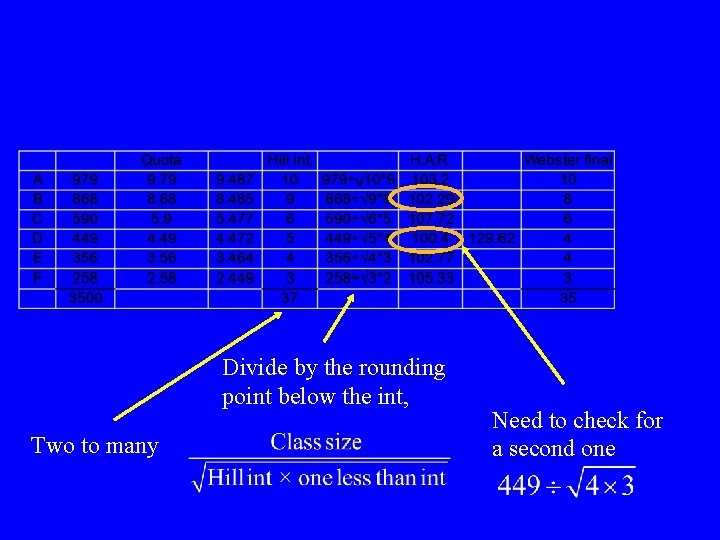
Divide by the rounding point below the int, Two to many Need to check for a second one
- Slides: 16