THE VIRTUAL FIELDS METHOD Professor Fabrice PIERRON Faculty

THE VIRTUAL FIELDS METHOD Professor Fabrice PIERRON Faculty of Engineering and the Environment Royal Society Wolfson Research Merit Award holder VFM course, BSSM conference, Sept. 1 st 2015

Course overview § Introduction and basic idea § Principle of virtual work § The Virtual Fields Method (VFM): principle in elasticity § Complements on the VFM § Match. ID demo (if time) § Conclusion Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 2/86

Introduction and basic idea

Introduction § Huge progress in computational mechanics – Simulation of machining · · Large strains elasto-plasticity Large strain rates Localization Friction/thermal behaviour § Problem – Many material parameters required – How to obtain them? Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 4/86

Introduction § Standard tests: Tensile test on rectangular specimen – Uniform stress state – Uniaxial stress strain curve s ? ? e – Very poor information – Very restrictive assumptions (constraints) Develop the experimental identification procedures of the future ! Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 5/86
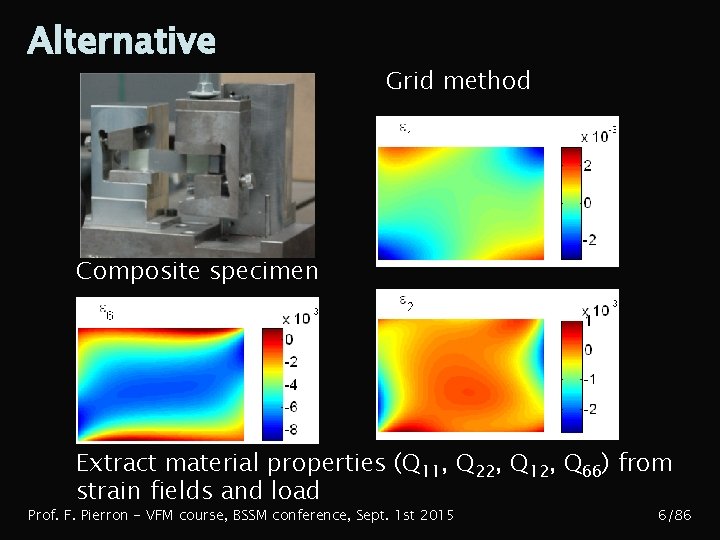
Alternative Grid method Composite specimen Extract material properties (Q 11, Q 22, Q 12, Q 66) from strain fields and load Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 6/86

Motivation § Extract more information from 1 test 0° tensile test 90° tensile test 3 tests 4 parameters shear test (off-axis) Local strain measurements Uniform stress fields (closed-form solution) Spatial stress distribution Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 7/86
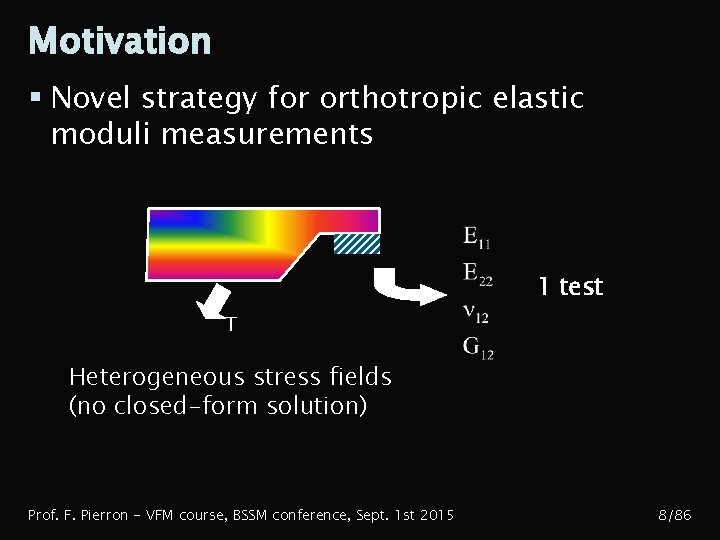
Motivation § Novel strategy for orthotropic elastic moduli measurements 1 test T Heterogeneous stress fields (no closed-form solution) Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 8/86

Motivation § Complex test geometry Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 9/86
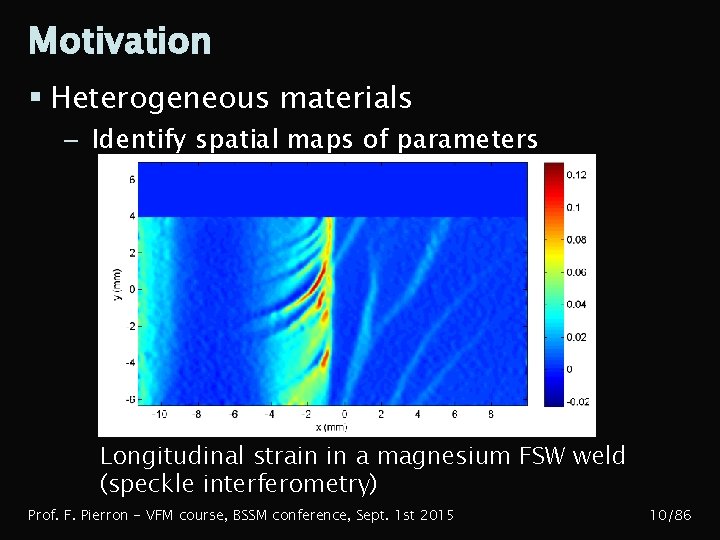
Motivation § Heterogeneous materials – Identify spatial maps of parameters Longitudinal strain in a magnesium FSW weld (speckle interferometry) Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 10/86

Key issues: full-field measurements § Why? – Complex strain state – Need for more experimental information § Interferometry (moiré, speckle, etc…) – High sensitivity, high spatial resolution – Small displacements (rigid body), low strains and high strain gradients § White light techniques – Image correlation : large displacements, 3 D – Grid method : intermediate Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 11/86

Key issues: full-field measurements § Extraordinary potential – From a few measurements points to a few 100. 000’s!! § Qualitative / quantitative ? – Metrological properties not fully assessed yet – Often reduced to visual information – Very few quantitative use of the data! § International effort – DIC Challenge (Society for Experimental Mechanics) https: //www. sem. org/dic-challenge/ Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 12/86

Key issues: inverse resolution § Extensive literature on inverse problems (mathematical) § Very few tools targeted at full-field processing § Very few groups with expertise in measurements and inverse problems at the same time § Inversion closely related to measurement performance! § Huge investigation area, critically underexplored Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 13/86

Inverse resolution § Basic equations I Equilibrium equations (static) + boundary conditions strong (local) or weak (global) II Constitutive equations (elasticity) III Kinematic equations (small strains/displacements) Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 14/86

Inverse resolution Known Direct problem Unknown Geometry Boundary conditions § Tools for solving this problem – – – Direct integration (closed-form solution) Approximate solutions Galerkin, Ritz Finite elements, boundary elements… etc… Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 15/86

Inverse resolution Known Inverse problem Unknown (measured) Geometry Some information on the boundary conditions (load cell) § Tools for solving this problem – Statically determined tests: Closed form solution of Eq. I (uncoupled system) Force BC, simple geometry Ex. : tensile test, bending tests (on rect. beams) etc… Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 16/86

Inverse resolution § Tools for solving this problem – Model updating Idea: iterative use of tool for direct problem (analytical or approximate) Example C 0 g = Fcost( - ) 0 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 17/86

Inverse resolution § Model updating – Advantages · General method (full-field measurements not compulsory) · Tools already developed – Shortcomings · Sensitive to boundary conditions (generally badly known) · CPU intensive (for numerical approximations and non-linear equations…) · Not fully dedicated to full-field measurements Alternative tool: the Virtual Fields Method Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 18/86

Basic idea § Use global equations (and not local) -F/2 x 2 -F/2 L F x 1 Integrate over x 2 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 19/86

Basic idea § Constitutive behaviour In-plane linear elastic isotropy Material is homogeneous Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 20/86

Basic idea § Surface measurements only Constant strains through the thickness ? is the surface of each pixel n is the number of strain data points If all pixels have the same size s (usually the case for CCD/CMOS based measurements) is the surface of the disc Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 21/86

Basic idea § Finally -F/2 x 2 -F/2 Integrate over x 1 L F x 1 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 22/86

Basic idea § What if the disc material is anisotropic? – Need for more equations § Tool to generate integral equilibrium equations: principle of virtual work Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 23/86

The principle of virtual work

The Principle of Virtual Work Equilibrium equation Boundary conditions on on Let be a vectorial function Integration over the whole domain Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 25/86

The Principle of Virtual Work § Integration by part and use of divergence theorem Virtual displacement field (cont. and diff) virtual strain tensor Applied stress vector on solid boundary External volume forces Stress tensor Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 26/86

Illustration of the PVW § Cantilever beam x 2 Section S F l x 1 L 0 thickness: e § Subsystem and FBD x 2 F l L 0 -x 1 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 x 1 27/86

Illustration of the PVW § Resultant of internal forces x 2 F A x l x 2 L 0 -x 1 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 x 1 28/86
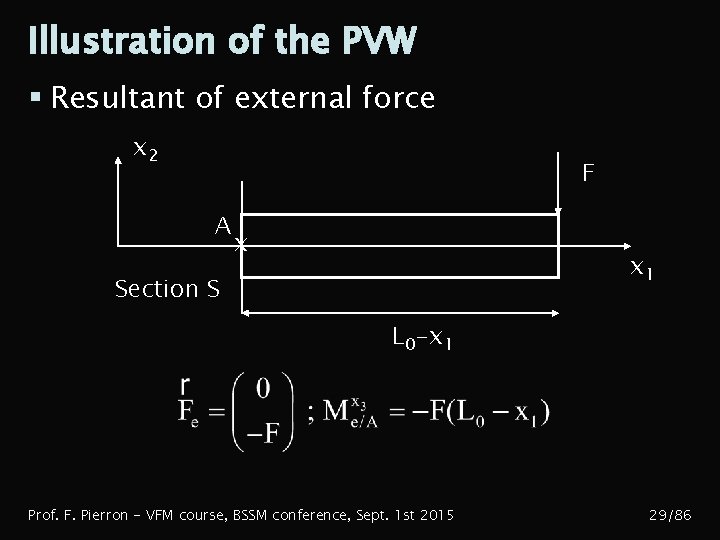
Illustration of the PVW § Resultant of external force x 2 F A x x 1 Section S L 0 -x 1 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 29/86

Illustration of the PVW § Equilibrium Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 30/86

Illustration of the PVW § Valid over any section S of the beam: – integration over x 1 Eq. 2 Eq. 3 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 31/86

Illustration of the PVW x 2 F l x 1 L 0 Principle of virtual work (static, no volume forces) Let us write a virtual field: Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 32/86

Illustration of the PVW x 2 F l x 1 L 0 Eq. 1 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 33/86
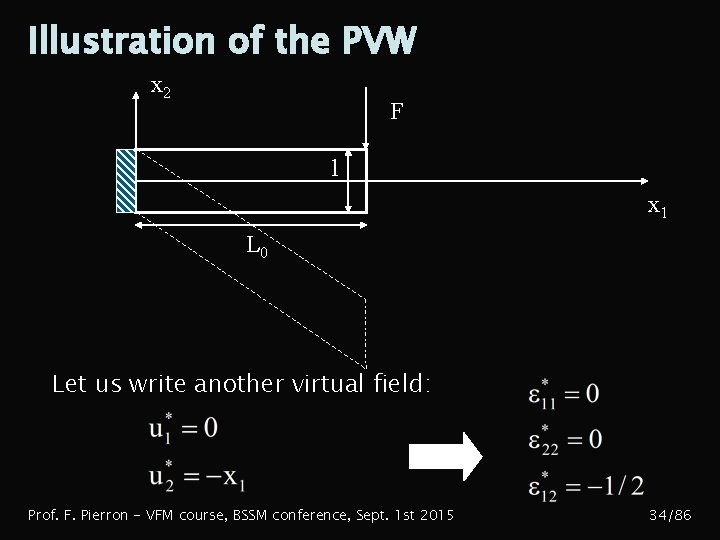
Illustration of the PVW x 2 F l x 1 L 0 Let us write another virtual field: Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 34/86

Illustration of the PVW x 2 F l x 1 L 0 Eq. 2 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 35/86

Illustration of the PVW x 2 F l x 1 L 0 Let us write a 3 rd field: virtual bending Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 36/86

Illustration of the PVW x 2 F l x 1 L 0 Eq. 3 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 37/86

Illustration of the PVW x 2 F l x 1 L 0 Any virtual field can be selected Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 38/86

The Virtual Fields Method
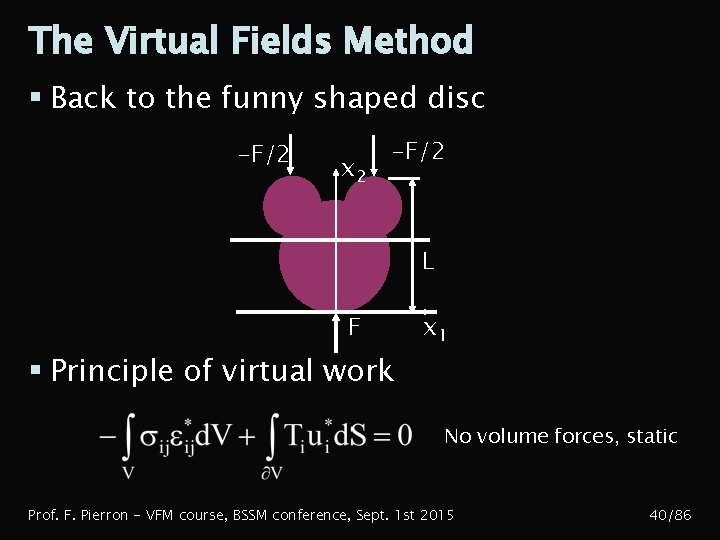
The Virtual Fields Method § Back to the funny shaped disc -F/2 x 2 -F/2 L F x 1 § Principle of virtual work No volume forces, static Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 40/86

The Virtual Fields Method § Let’s write two virtual fields – 1 st virtual field: virtual compression field -F/2 x 2 -F/2 L F Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 x 1 41/86

The Virtual Fields Method § 2 nd virtual field: transverse shrinking § Other virtual fields (an infinity!) Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 42/86

The Virtual Fields Method § Principal advantages – Independent from stress distribution; etc. geometry – Direct identification in elasticity (no updating) § Limitations – Kinematic assumption through the thickness (plane stress, plane strain, bending. . . ) Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 43/86

VFM: more complex example § Orthotropic elasticity x 2 x 1 Orthotropic material Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 44/86

VFM: more complex example x 2 x 1 Choice of the virtual fields 1. Measurement on S 2 only (optical system) Over S 1 and S 3: (rigid body) 2. A priori choice: over S 1: Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 45/86

VFM: more complex example x 2 T 2 i x 1 T 1 i Unknown force distribution over S 1 and S 3. Resultant P measured 3. Over S 3 (rigid body) : 2 possibilities 3. 1 3. 2 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 46/86
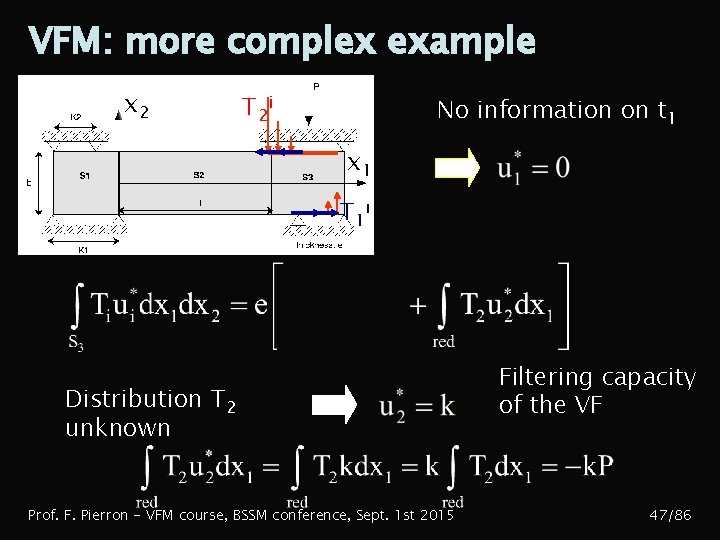
VFM: more complex example x 2 T 2 i No information on t 1 x 1 T 1 i Distribution T 2 unknown Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 Filtering capacity of the VF 47/86
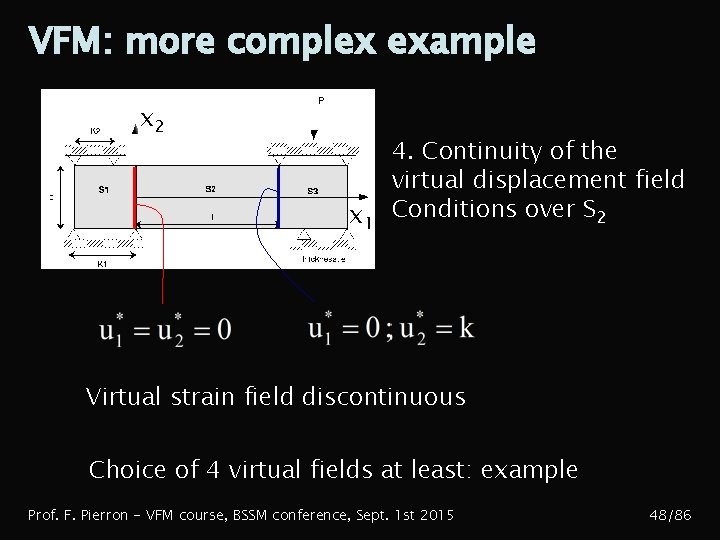
VFM: more complex example x 2 x 1 4. Continuity of the virtual displacement field Conditions over S 2 Virtual strain field discontinuous Choice of 4 virtual fields at least: example Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 48/86
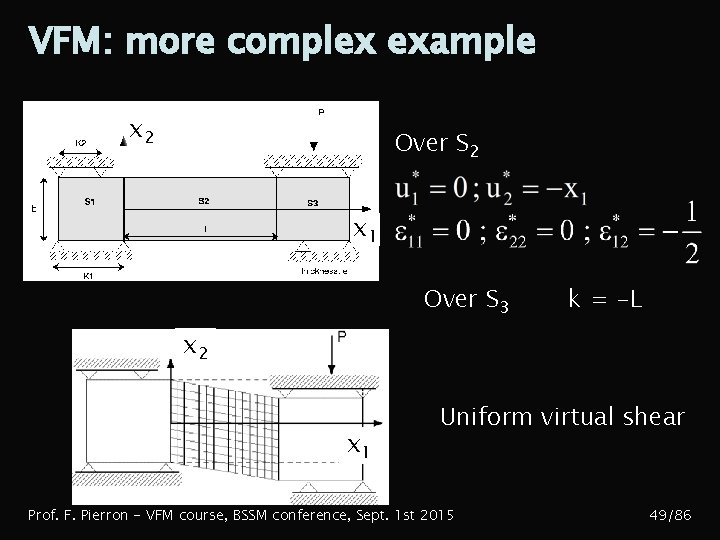
VFM: more complex example x 2 Over S 2 x 1 Over S 3 k = -L x 2 x 1 Uniform virtual shear Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 49/86

VFM: more complex example Plane stress orthotropic elasticity Plane stress Homogeneous material Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 50/86
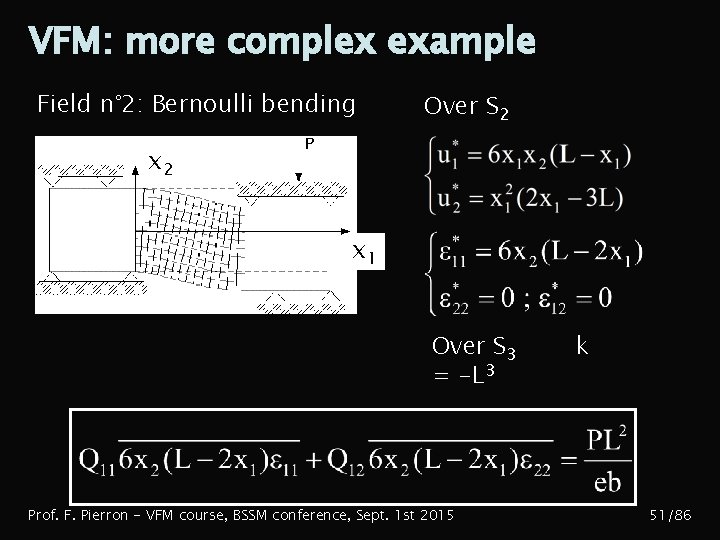
VFM: more complex example Field n° 2: Bernoulli bending Over S 2 x 1 Over S 3 = -L 3 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 k 51/86
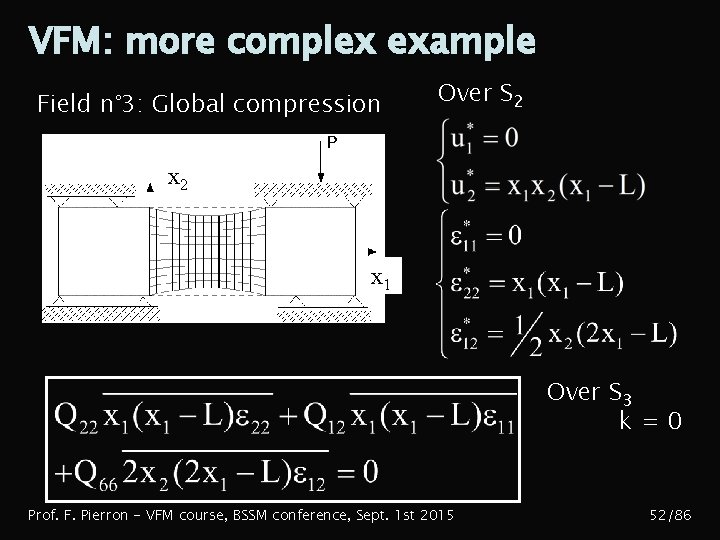
VFM: more complex example Field n° 3: Global compression Over S 2 x 1 Over S 3 k=0 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 52/86

VFM: more complex example Field n° 4: Local compression Over A 1 x 2 x 1 Over A 2 Over S 3 k = 0 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 53/86

VFM: more complex example Field n° 4: Local compression Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 54/86

VFM: more complex example Final system AQ = B Q = A-1 B If VF independent !! Pierron F. et Grédiac M. , Composites Part A, vol. 31, pp. 309 -318, 2000. Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 55/86

Complements on the VFM

Summary § Virtual fields selection in elasticity § Heterogeneous materials § Non-linear constitutive models § Dynamics § Force identification § Equilibrium gap Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 57/86

VF selection

VF selection § Exact data – All sets of VF produce the SAME results § Noisy data – Different sets provide different results – Optimal selection? Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 59/86

VF selection § Strategy for virtual fields selection in elasticity – Projection of VF on a certain basis of functions – Polynomial – Choice of VF: choice of a set of m, n, aij, bij Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 60/86

VF selection § Strategy to find aij, bij for given m and n – Special virtual fields – For instance, special virtual field to identify Q 11 =1 =0 =0 =0 – 4 linear equations linking the aij and bij coefficients – Virtual BCs: a few more linear equations – Still a very large number of VF in general! Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 61/86

VF selection § Strategy to find aij, bij for given m and n – Minimization of the sensitivity to noise – Constrained minimization problem where aij and bij coefficients are the unknown – Provides the maximum likelihood solution, with: is the standard deviation of strain noise are the sensitivity to noise coefficients Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 62/86
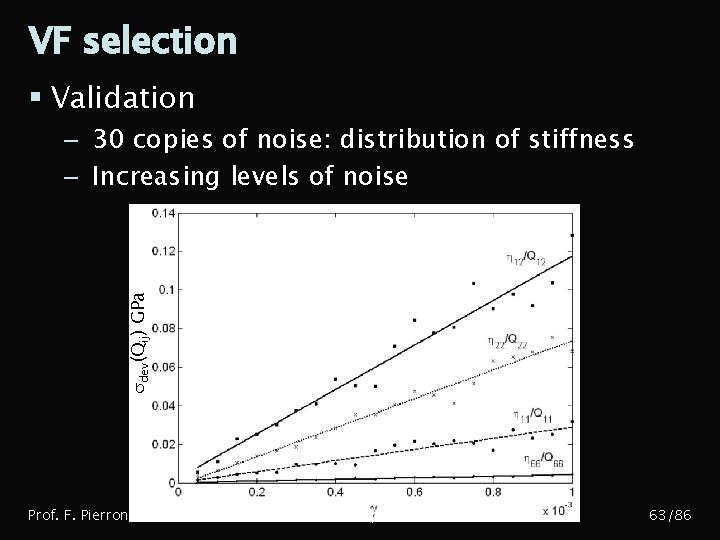
VF selection § Validation sdev(Qij) GPa – 30 copies of noise: distribution of stiffness – Increasing levels of noise Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 63/86

VF selection § Actual and virtual optimized virtual fields for Q 11 (m=4, n=5) Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 64/86

VF selection § Piecewise virtual fields – Finite element mesh – Virtual Dofs unknown of minimization problem Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 65/86

VF selection § Piecewise virtual fields – Advantage: more flexible – Easy for virtual BCs All dofs To zero Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 All u 1*=0 All u 2*=cst 66/86
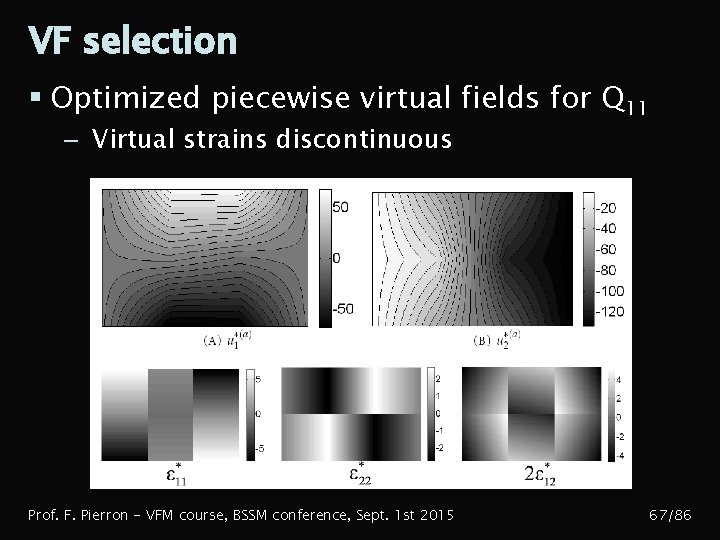
VF selection § Optimized piecewise virtual fields for Q 11 – Virtual strains discontinuous Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 67/86

Heterogeneous materials

Heterogeneous materials § Discrete parameterization – Multimaterials – Sharp transitions C 2 C 3 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 C 1 69/86

Heterogeneous materials § Discrete parameterization – 6 unknowns in isotropic linear elasticity – Contrast of stiffness: strain derivative!! – Subject to noise Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 70/86

Heterogeneous materials § Continuous parameterization – Functionally graded material – Smooth transitions x 2 C=f(x 2) – Polymer/composite with moisture ingress from one face – Ceramic with varying pore density – Etc… Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 71/86

Heterogeneous materials § Continuous parameterization x 2 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 72/86

Heterogeneous materials § Mixed parameterization – Plate with local damage or manufacturing defect C 1 C 2=f(r) Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 73/86

Non-linear constitutive model
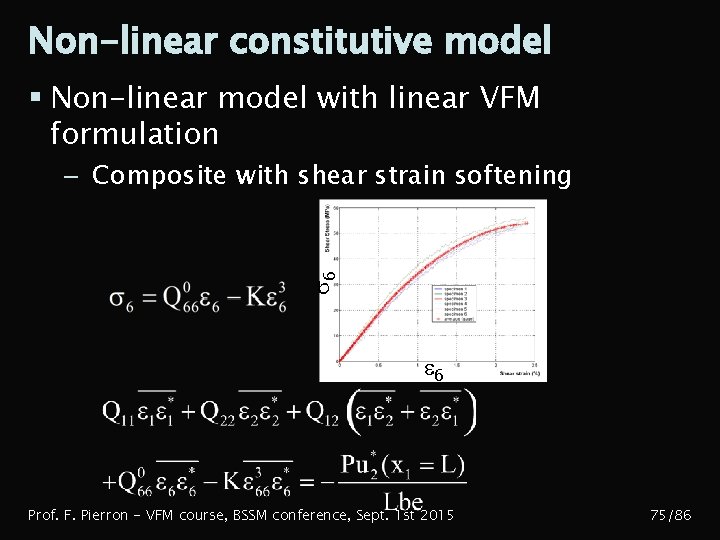
Non-linear constitutive model § Non-linear model with linear VFM formulation s 6 – Composite with shear strain softening e 6 Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 75/86

… in elasto-plasticity § Virtual fields method for non-linear constitutive equations Measured: Iterative but no direct problem solved Fast (minutes) Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 76/86

Dynamics

VFM in dynamics § Principle of virtual work in dynamics x 2 L F(t) If the load is unknown x 1 In statics: with other virtual fields Only stiffness ratios can be identified (Poisson’s ratio) Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 78/86

VFM in dynamics x 2 L F(t) Measurements x 1 Single spatial differentiation Double temporal differentiation Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 79/86
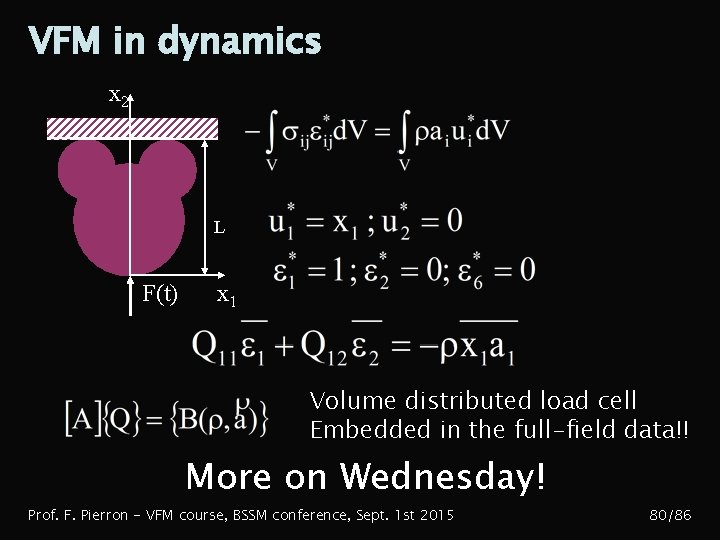
VFM in dynamics x 2 L F(t) x 1 Volume distributed load cell Embedded in the full-field data!! More on Wednesday! Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 80/86

Force identification

Force identification § Standard VFM Measured § Force VFM Measured Unknown Berry, A. , Robin, O. , & Pierron, F. (2014). Journal of Sound and Vibration, 333(26), 7151 -7164. Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 82/86

Equilibrium gap
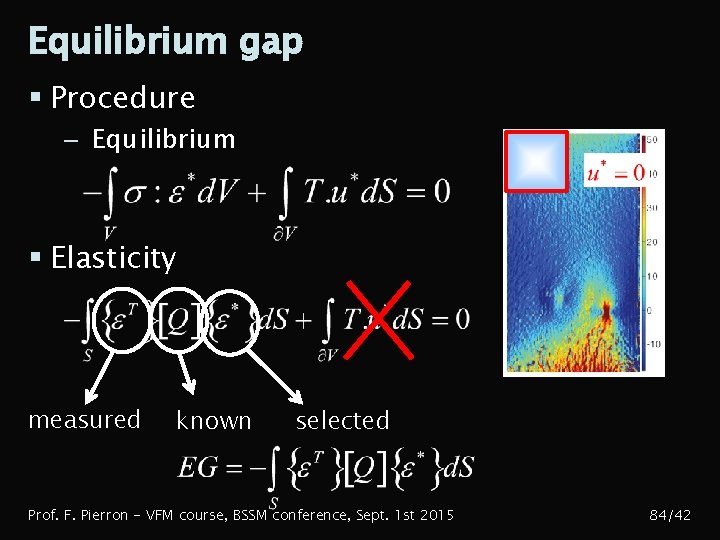
Equilibrium gap § Procedure – Equilibrium § Elasticity measured known selected Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 84/42

Equilibrium gap § Choice of the virtual field – Piecewise functions k data points § What is detected? – – – Bad strain data Inaccurate material parameters Inappropriate material model Damage … n data points Spatial map of Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 85/42

Conclusion

Conclusion § VFM: operational tool, computationally simple and efficient § Future challenges – Design and optimize test configurations, predict error bars (new operational standards) – Apply to 3 D (X-ray CT + DVC) – High rate dynamics (see talk on Tuesday) – Optimization of VFs for non-linear VFM – Integrate with measurements: Match. ID platform Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 87/86
Match. ID § www. match. IDmbc. com Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 88/86

More on the VFM § Theory § Applications § Self-training Prof. F. Pierron - VFM course, BSSM conference, Sept. 1 st 2015 89/86
- Slides: 89