The Variance of a Random Variable Lecture 35

The Variance of a Random Variable Lecture 35 Section 7. 5. 1 Fri, Mar 26, 2004

The Variance of a Discrete Random Variable – The square of the standard deviation of that random variable. n The variance of X is denoted by 2 or Var(X) n The standard deviation of X is denoted by . n

The Variance and Expected Values The variance is the expected value of the squared deviations. n That agrees with the earlier notion of the average squared deviation. n Therefore, Var(X) = E((X – µ)2). n

Example of the Variance n Again, let X be the number of children in a household. x P(X = x) 0 1 2 0. 10 0. 30 0. 40 3 0. 20

Example of the Variance n Subtract the mean (1. 70) from each value of X to get the deviations. x P(X = x) x–µ 0 1 2 0. 10 0. 30 0. 40 -1. 7 -0. 7 +0. 3 3 0. 20 +1. 3
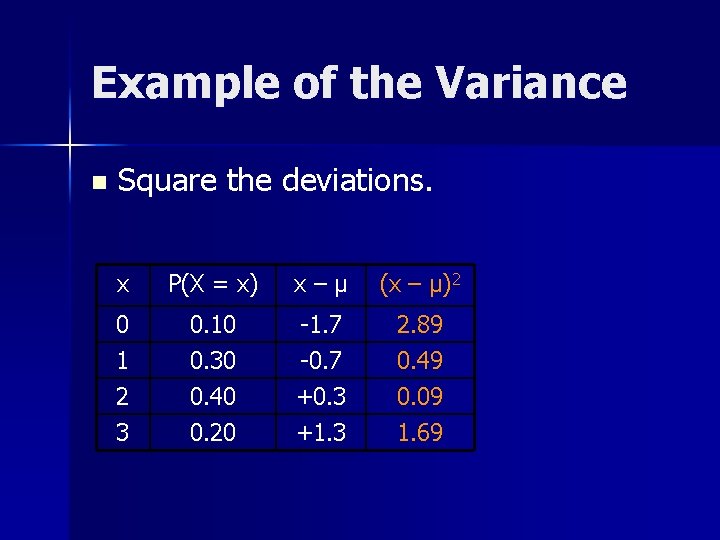
Example of the Variance n Square the deviations. x P(X = x) x–µ (x – µ)2 0 1 2 0. 10 0. 30 0. 40 -1. 7 -0. 7 +0. 3 2. 89 0. 49 0. 09 3 0. 20 +1. 3 1. 69
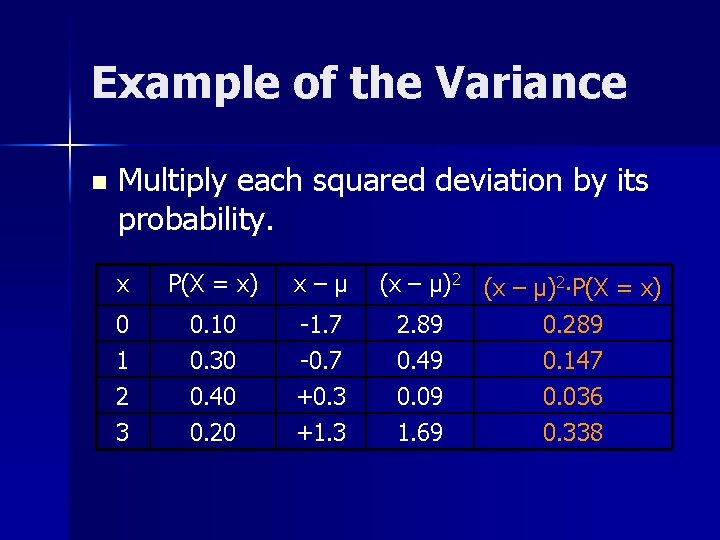
Example of the Variance n Multiply each squared deviation by its probability. x P(X = x) x–µ 0 1 2 3 0. 10 0. 30 0. 40 0. 20 -1. 7 -0. 7 +0. 3 +1. 3 (x – µ)2 P(X = x) 2. 89 0. 49 0. 09 1. 69 0. 289 0. 147 0. 036 0. 338

Example of the Variance n Add up the products to get the variance. x P(X = x) x–µ 0 1 2 3 0. 10 0. 30 0. 40 0. 20 -1. 7 -0. 7 +0. 3 +1. 3 (x – µ)2 P(X = x) 2. 89 0. 49 0. 09 1. 69 0. 289 0. 147 0. 036 0. 338 0. 810 = 2

Example of the Variance n Add up the products to get the variance. x P(X = x) x–µ 0 1 2 3 0. 10 0. 30 0. 40 0. 20 -1. 7 -0. 7 +0. 3 +1. 3 (x – µ)2 P(X = x) 2. 89 0. 49 0. 09 1. 69 0. 289 0. 147 0. 036 0. 338 0. 810 = 2 0. 9 =

Exercise Let’s Return To Let’s Do It! 7. 23, p. 430. n The variance of Profit Indoors is Var(Profit Indoors) = 29. 0 n Compute the variance of Profit Outdoors. n Which setting (indoors or outdoors) exhibits the greater variability? n

Alternate Formula for the Variance It turns out that Var(X) = E(X 2) – (E(X))2. n That is, the variance of X is “the expected value of the square of X minus the square of the expected value of X. ” n Of course, we could write this as Var(X) = E(X 2) – µ 2. n

Example of the Variance n One more time, let X be the number of children in a household. x 0 P(X = x) 0. 10 1 2 3 0. 30 0. 40 0. 20

Example of the Variance n Square each value of X. x 0 P(X = x) 0. 10 x 2 0 1 2 3 0. 30 0. 40 0. 20 1 4 9

Example of the Variance n Multiply each squared X by its probability. x 0 P(X = x) 0. 10 x 2 P(X = x) 0. 00 1 2 3 0. 30 0. 40 0. 20 1 4 9 0. 30 1. 60 1. 80

Example of the Variance n Add up the products to get E(X 2). x 0 P(X = x) 0. 10 x 2 P(X = x) 0. 00 1 2 3 0. 30 0. 40 0. 20 1 4 9 0. 30 1. 60 1. 80 3. 70 = E(X 2)

Example of the Variance Then use E(X 2) to compute the variance. n Var(X) = E(X 2) – µ 2 = 3. 70 – (1. 7)2 = 3. 70 – 2. 89 = 0. 81. n It follows that = 0. 81 = 0. 9. n

Exercise Return once more to Let’s Do It! 7. 23, p. 430. n Use the alternate formula to compute the variance of Profit Indoors. n

Means and Standard Deviations on the TI-83 n n n n Store the list of values of X in L 1. Store the list of probabilities of X in L 2. Select STAT > CALC > 1 -Var Stats. Press ENTER. Enter L 1, L 2. Press ENTER. The list of statistics includes the mean and standard deviation of X.

Means and Standard Deviations on the TI-83 Let L 1 = {0, 1, 2, 3}. n Let L 2 = {0. 1, 0. 3, 0. 4, 0. 2}. n Compute the statistics. n Compute µ and for the Indoor and Outdoor distributions in Let’s Do It! 7. 23, p. 430. n

Assignment Page 442: Exercise 56. n Page 451: Exercises 91*, 93*, 94*, 95*, 96*. * Find the variance and standard deviation. n
- Slides: 20