The use of High Performance Computing in Astrophysics

The use of High Performance Computing in Astrophysics: an experience report Paolo Miocchi in collaboration with R. Capuzzo-Dolcetta, P. Di Matteo, A. Vicari Dept. of Physics, Univ. of Rome “La Sapienza” (Rome, Italy) Work supported by the INAF-CINECA agreement (http: //inaf. cineca. it, grant inarm 033).

The needs of HPC in Globular Cluster dynamics Theoretical study of a system made up of N ~ 105 – 107 gravitationally bound stars (Self-gravitating system).

The needs of HPC in Globular Cluster dynamics Theoretical study of a system made up of N ~ 105 – 107 gravitationally bound stars (Self-gravitating system). ß O(N 2 ) force computations to do.

The needs of HPC in Globular Cluster dynamics Gravity is a long-range and attractive force ß Ø Very unstable dynamical states

The needs of HPC in Globular Cluster dynamics Gravity is a long-range and attractive force ß Ø Inhomogeneous mass distributions very wide range of Individual and ß variable time-steps – 1/2 should be adopted time-scales ~ (G ) ß Numerically “expensive” time integration of particle motion

The needs of HPC in Globular Cluster dynamics Gravity is a long-range and attractive force ß Ø Ø Ø Very unstable dynamical states Inhomogeneous mass distributions 3 D problems! ß arduous analytical approach!

The needs of HPC in Globular Cluster dynamics Dynamical evolution of self-gravitating systems with N > 105 stars ß > tens of Gflops needed! ß codes PARALLELIZATION required

The tree-code n particles M = tot. mass Q = quadrupole F m r cm m computational cost independent of n see Barnes & Hut 1986, Nature 324, 446

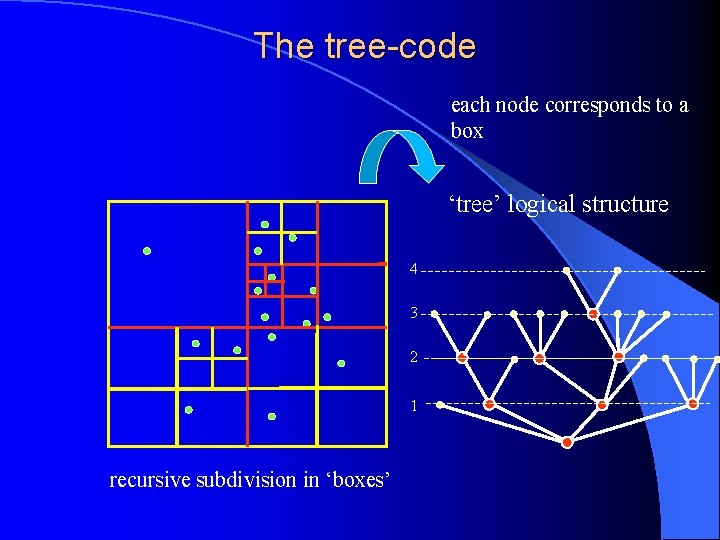
The tree-code each node corresponds to a box ‘tree’ logical structure 4 3 2 1 recursive subdivision in ‘boxes’

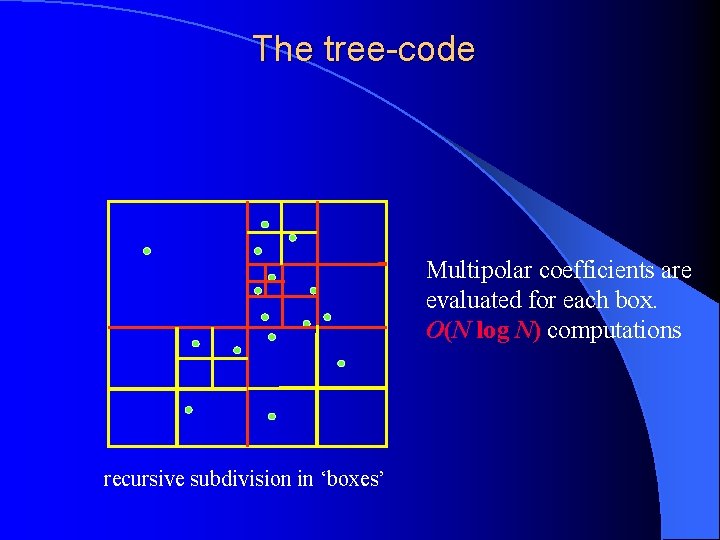
The tree-code Multipolar coefficients are evaluated for each box. O(N log N) computations recursive subdivision in ‘boxes’

Problems in the tree-code parallelization Gravity is a long range interaction: inter-processor data transfer unavoidable (heavy overhead on DMP) Ø Inhomogeneous mass distributions: particles assignment to PEs has to be done according to the workload Ø Hierarchical force evaluation: most of force contributions due to closer bodies, spatial domain decomposition. Ø

the ‘Adaptive Tree Decomposition’ method Ø Ø Ø Domain decomposition is performed ‘on-the-fly’ during the tree-construction with a low computational cost. The adaptivity of the tree structure is exploited to give a good load-balancing and data-locality in the forces evaluation. The locally essential tree is built ‘dynamically’ during the tree-walking: remote boxes are linked only when really needed.

the ‘Adaptive Tree Decomposition’ method UPPER-TREE: many boxes with few particles inside. LOWER-TREE: few boxes containing many particles. Two different parallelization strategies see Miocchi & Capuzzo-Dolcetta 2002, A&A 382, 758 PE 0 1 2 3

the ‘Adaptive Tree Decomposition’ approach Some definitions Ø Ø Ø UPPER-tree = made up of boxes with less than kp particles inside; LOWER-tree = made up of boxes with more than kp particles; a Pseudo-terminal (PTERM) box is a box in the upper-tree whose ‘parent box’ is in the lower-tree; p = no. of processors, k = fixed coefficient

the ‘Adaptive Tree Decomposition’ method Parallelization of the lower-tree construction. . . 1. Preliminary “random” particles distribution to PEs. 2. All PEs work, starting from the root box, constructing in synchrony the same lower-boxes (by a recursive procedure). 3. When a PTERM box is found, it is assigned to a certain PE (so to preserve a good load-balancing in the subsequent forces evaluation) and no further ‘branches’ are built up. domain decomposition: Communications among PEs during tree-walking are minimized by the particular order in which PTERM boxes are met. The lower-tree is stored in the local memories of ALL PEs. load balancing: in this stage it is ensured by setting k sufficiently large so to deal always with a number of particles in a box much greater than the number of processors.

the ‘Adaptive Tree Decomposition’ method PTERM order Example of a uniform 2 -D distribution with PTERM boxes at the 3 rd subdivision level. Every spatial domain is (nearly) contiguous the data transfer among PEs is minimized

the ‘Adaptive Tree Decomposition’ method Example of domain decomposition Plummer distribution of 16 K particles; 4 processors

the ‘Adaptive Tree Decomposition’ method Parallelization of the upper-tree construction Ø Ø PTERM boxes have been already distributed to PEs Each PE works independently and asynchronously, starting from every PTERM box in the domain and building the descendant portion of the upper-tree, up to the terminal boxes.

the ‘Adaptive Tree Decomposition’ method Parallelization of the tree walking Ø Ø Ø Each PE evaluates independently the forces on the particles belonging to its domain (i. e. those contained in the PTERM boxes previously assigned). Each PE has in its memory the local tree, i. e. the whole lower-tree plus the portion of the upper-tree that is descended from the PTERM boxes of the PE’s domain. When a ‘remote’ box is met, it is linked to the local tree, copying it into the local memory.

Code performance on a IBM SP 4 Performances on one ‘main’ time-step (T ) with complete forces evaluation and time integration of motion for a selfgravitating system with N = 106 particles WARNING Ø each particle has its own variable time-step depending on the local density of mass and typical velocity. Ø Dynamical tree recostruction implemented The tree is re-built when the no. of interactions evaluated is > N /10 (Springel et al. , 2001, New Astr. , 6, 51) according to the block time scheme the particle step can be T/2 n (Aarseth 1985)

Code performance on a IBM SP 4 Performance on one ‘main’ time-step (T ) with complete forces evaluation and time integration of motion for a self-gravitating system with N = 106 particles 2, 100, 000 timeadvancing performed

Code performance on a IBM SP 4 Performance on one ‘main’ time-step with complete forces evaluation and time integration of motion for a self-gravitating system with N = 106 particles ( = 0. 7, k = 256, up to 16 PEs per node) CPU-time (sec) 25, 000 particles per second

Code performance on a IBM SP 4 Ø The speedup behaviour is very good up to 16 PEs (= 10). Ø The load-unbalancing is low (10% with 64 PEs). Ø Data transfer and communications still penalize the overall performance with low PEs / N ratio (34% with 64 PEs). Ø An MPI-2 version could fully exploit the ATD parallelization strategy.

Merging of Globular Clusters in galactic central regions Motivation: the study of the dynamical evolution and the fate of young GCs within the bulge Ø Ø Ø To what extent can GCs survive the strong tidal bulge interaction? Do they merge at the end? § What features the final merging product will have? To what extent can the bulge accrete from the GCs mass lost?

Merging of Globular Clusters in galactic central regions Motivation: the study of the dynamical evolution and the fate of young GCs within the bulge 30, 000 CPU-hours on an IBM SP 4 provided by the INAF-CINECA agreement for a scientific ‘keyproject’ (under grant inarm 033)

Merging of Globular Clusters in galactic central regions Features of the numerical approach Ø Ø Ø N-body (tree-code) accurate simulations with high number of ‘particles’ (106). Dynamical friction and mass function included. Self-consistent triaxial bulge model (Schwarzschild). A B c rc (pc) tcr (Kyr) (km/s) a 20 95 0. 8 14 170 33 b 15 72 0. 9 9 100 33 c 20 98 1. 2 5. 5 42 37 d 15 77 1. 3 3. 8 28 37 higher concentration Simulation cluster M (106 M ) rt (pc)

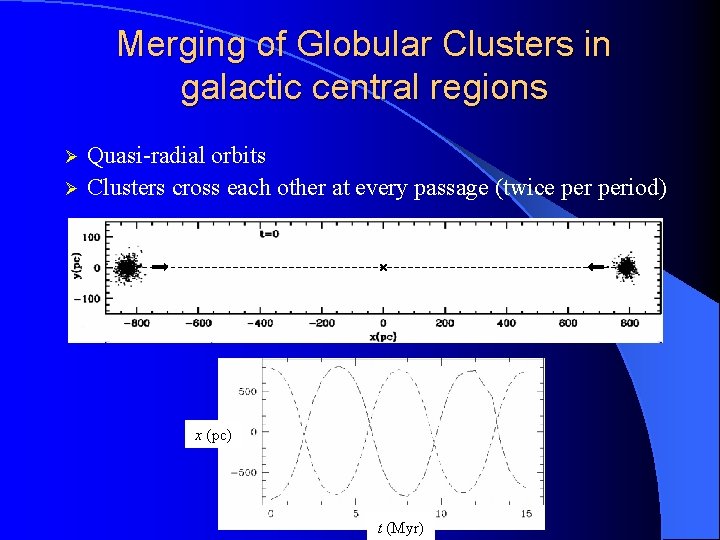
Merging of Globular Clusters in galactic central regions Ø Ø Quasi-radial orbits Clusters cross each other at every passage (twice period) x (pc) t (Myr)

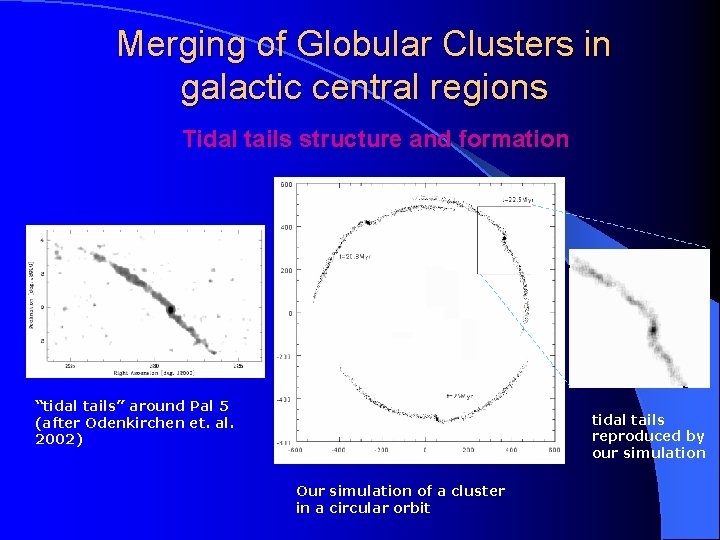
Merging of Globular Clusters in galactic central regions Tidal tails structure and formation “tidal tails” around Pal 5 (after Odenkirchen et. al. 2002) tidal tails reproduced by our simulation Our simulation of a cluster in a circular orbit

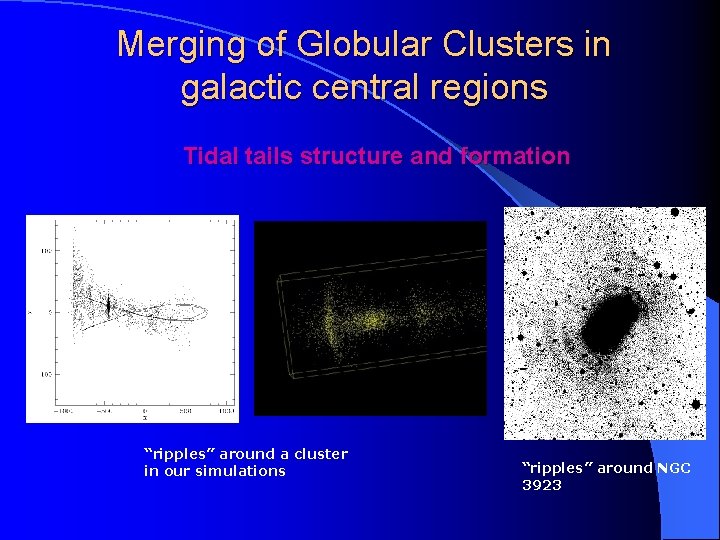
Merging of Globular Clusters in galactic central regions Tidal tails structure and formation “ripples” around a cluster in our simulations “ripples” around NGC 3923

Merging of Globular Clusters in galactic central regions Tidal tails structure and formation What “ripples” are? How do they form? 3 D visualization tools can help to give answers! “ripples” around a cluster “ripples” around NGC 3923

Merging of Globular Clusters in galactic central regions Density profiles of the most compact cluster (solid lines) fitted with a single-mass King model (dotted lines) tidal tails t=0 t = 17 Myr (dashed black line: bulge central density) least compact cluster at t = 15 Myr

Merging of Globular Clusters in galactic central regions Fractiono f mass lost E = fraction of mass lost if Ei > 0 p = fraction of mass lost if / < p/100 1. 3 central cluster density 0. 9 c = 0. 8 1. 2 bulge stellar density