The Unscented Kalman Filter UKF Chapter 7 a

The Unscented Kalman Filter (UKF) Chapter 7 a Rudolf E. Kalman Hao Liu Ke Zhang 1 Introduction to Kalman filtering TRAIL Course on Kalman filtering

Contents of Chapter 7 Part A: • 7. 1 Introduction • 7. 2 Optimal Recursive Estimation & the EKF • 7. 3 The Unscented Kalman Filter • 7. 4 UKF Parameter Estimation • 7. 5 UKF Dual Estimation Part B: • 7. 6 The Unscented Particle Filter (Presented by other group next week) Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 2

Main Issues in Chap. 7 A Why UKF is Needed What can UKF Do Who Contribute to UKF How does UKF Work The UKF Algorithms The Applications of UKF Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 3

Outline Introduction & Methodology (Presented by Ke) Why UKF is Needed What can UKF Do Who Contribute to UKF How does UKF Work Algorithms & Applications (Presented by Hao) Algorithms UKF State Estimation UKF Parameter Estimation UKF Dual Estimation Applications Two Examples realized by MATLAB Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 4

Quick Review of the Former Presentations Kalman Filter (KF) – Chapter 1 Linear dynamical system (Linear evolution functions) Extended Kalman Filter (EKF) – Chapter 1 Non-linear dynamical system (Non-linear evolution functions) Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 5

Extended Kalman filter (Chapter 1) • Consider the following non-linear system: • Assume that we can somehow determine a reference trajectory • Then: • where Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering EKF uses first order terms of the Taylor series expansion of the nonlinear functions. 6

Extended Kalman filter (Chapter 1) • For the measurement equation, we have: • We can then apply the standard Kalman filter to the linearized model • How to choose the reference trajectory? • Idea of the extended Kalman filter is to re-linearize the model around the most recent state estimate, i. e. Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 7

Extended Kalman Filter (Chapter 1) • Time-propagation (prediction): • Measurement adaptation (correction): • Kalman gain: Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 8

Use of Extended Kalman filter The Extended Kalman Filter (EKF) has become a standard technique used in a number of nonlinear estimation and machine learning applications State estimation (Chapter 1) estimating the state of a nonlinear dynamic system Parameter estimation (Chapter 2) estimating parameters for nonlinear system identification e. g. , learning the weights of a neural network dual estimation (Chapter 5) both states and parameters are estimated simultaneously e. g. , the Expectation Maximization (EM) algorithm Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 9

Comments on EKF The Extended Kalman Filter (EKF) has long been the de-facto standard for nonlinear state space estimation simplicity, robustness and suitability for real-time implementations Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 10

A Basic Flaw of Extended Kalman filter The state distribution is approximated by a Gaussian Random Variables, which is then propagated analytically through the “first-order’ linearization of a nonlinear system. These approximations can introduce large errors in the true posterior mean and covariance of the transformed (Gaussian) random variable, especially when the models are highly nonlinear, which may lead to suboptimal performance sometimes divergence of the filter Local linearity assumption breaks down when the higher order terms become significant. Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 11

Introduction to the Alternative Approach —— the Unscented Kalman Filter (UKF) UKF is an improvement on EKF A central and vital operation performed in the Kalman Filter is the propagation of a Gaussian random variable (GRV) through the system dynamics EKF the state distribution is approximated by a GRV which is then propagated analytically through the first-order linearization of the nonlinear system. UKF The UKF addresses EKF’s problem by using a deterministic sampling approach This filter claims both higher accuracy and robustness for nonlinear models Remarkably, the computational complexity of the UKF is the same order as that of the EKF Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 12

Idea of UKF The state distribution is again approximated by a GRV, but is represented using a minimal set of carefully chosen sample points. These sample points completely capture the true mean and covariance of the GRV and when propagated through the true nonlinear system, captures the posterior mean and covariance accurately to the 3 rd order (Taylor series expansion) for any nonlinearity Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 13

The development of UKF S. J. Julier and J. K. Uhlmann, A New Extension of the Kalman Filter to Nonlinear Systems, 1997 demonstrated the substantial performance gains of the UKF in the context of state-estimation for nonlinear control Machine learning problems were not considered Eric A. Wan and Rudolph van der Menve, The Unscented Kalman Filter for Nonlinear Estimation, 2000 extend the use of the UKF to a broader class of nonlinear estimation problems, including nonlinear system identification training of neural networks and dual estimation problems Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 14

What is UKF is a straightforward transformation application of the unscented Unscented Transformation The unscented transformation (UT) is a method for calculating the statistics of a random variable which undergoes a nonlinear transformation builds on the principle that it is easier to approximate a probability distribution than an arbitrary nonlinear function Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 15

Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 16

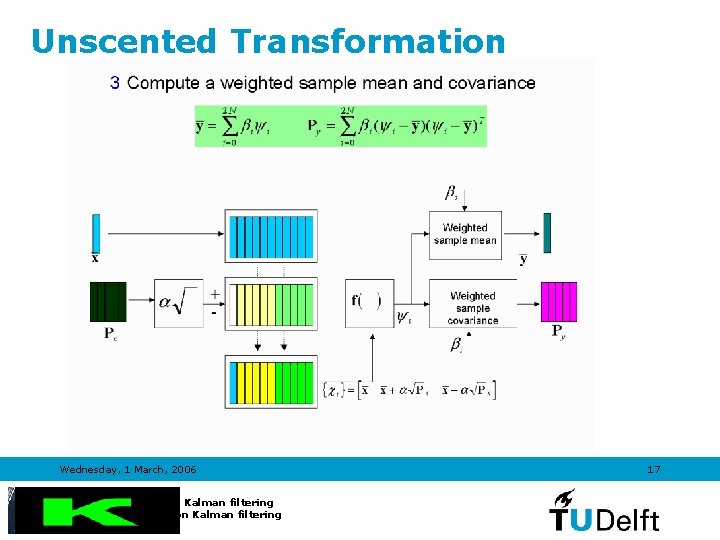
Unscented Transformation Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 17

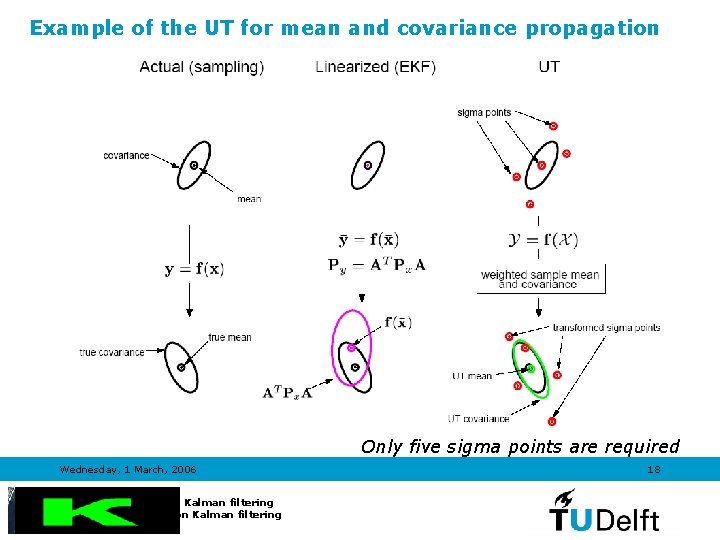
Example of the UT for mean and covariance propagation Only five sigma points are required Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 18

Definition of Sigma Points Assume has mean A set of and covariance weighted samples or sigma points are chosen as follows: Where is a scaling parameter The constant determines the spread of the sigma points around and is usually set to a small positive value (e. g. , ). The constant is a secondary scaling parameter which is usually set to 3 -L is used to incorporate prior knowledge of the distribution of x (for Gaussian distributions, is optimal) is the i th column of the matrix square root of Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 19

Propagation of Sigma Points Each sigma point is propagated through the nonlinear function and the estimated mean and covariance of y are computed as follows These estimates of the mean and covariance are accurate to the second order of the Taylor series expansion of for any nonlinear function Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 20

What can UKF do State Estimation of a discrete-time nonlinear dynamic system Parameter Estimation in a nonlinear mapping Dual Estimation of a discrete-time nonlinear dynamic system Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 21

Advantage of Unscented Kalman Filter Approximates the distribution rather than the nonlinearity Accurate to at least the 2 nd order (3 rd for Gaussian inputs) No Jacobians or Hessians are calculated, same computational complexity as EKF Efficient “sampling” approach Weights β and α can be modified to capture higher-order statistics Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 22

UKF Algorithm • State estimation • Parameter estimation • Dual UKF • An interesting topic • Questions for discussion Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 23

UKF Algorithm • State estimation • Parameter estimation • Dual UKF • An interesting topic • Questions for discussion Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 24

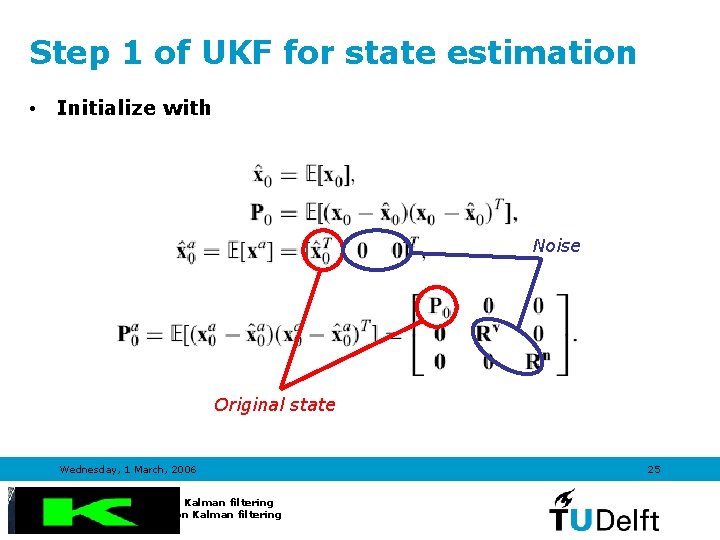
Step 1 of UKF for state estimation • Initialize with Noise Original state Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 25

Step 2 of UKF for state estimation • Calculate the sigma points • Weight states and outputs of sigma points Weighted State Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering Weighted Output 26

Step 2 of UKF for state estimation • Weight covariance with respect to states Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 27

Step 3 of UKF for state estimation • Weight covariance with respect to outputs • Weight covariance with respect to states and outputs Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 28

Step 4 of UKF for state estimation • Update state and state covariance Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 29

Implementation Variations • UKF-additive (zero mean) noise case Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 30

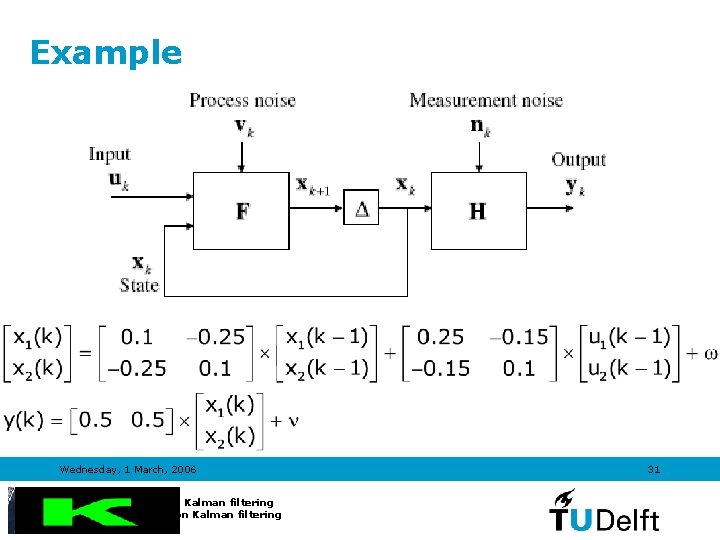
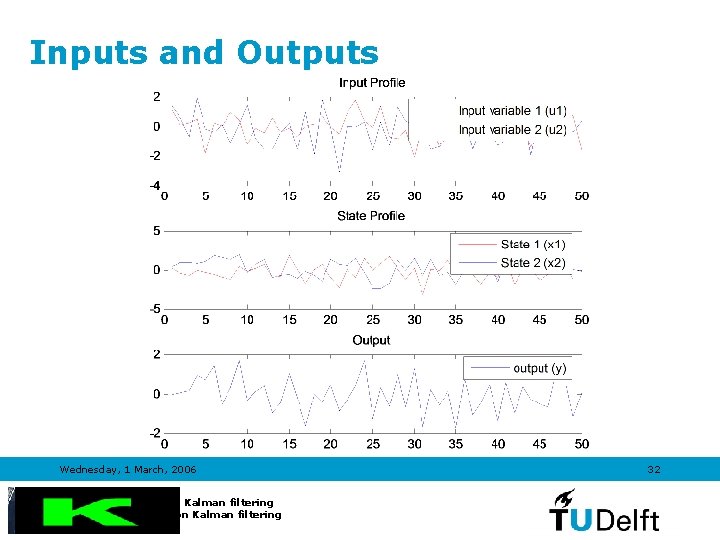
Example Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 31

Inputs and Outputs Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 32

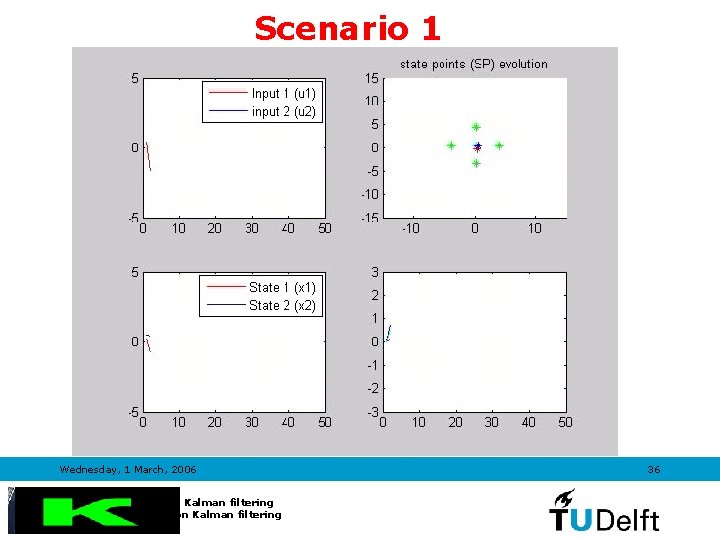
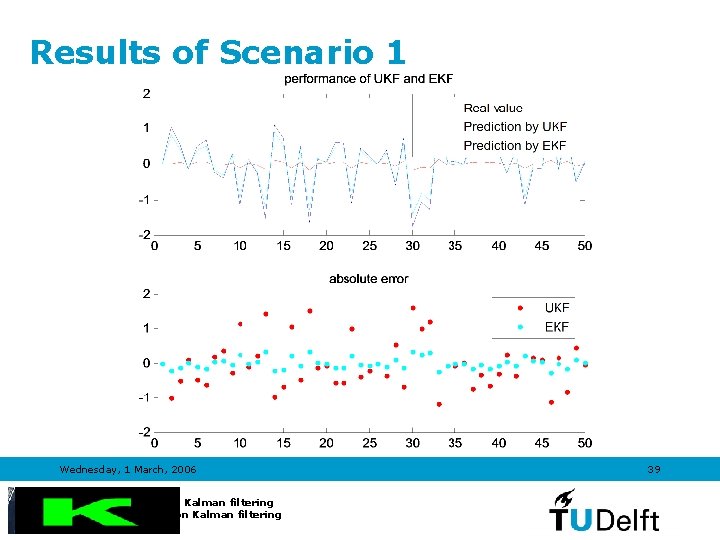
Scenario 1 • UKF • EKF Process noise covariance Qh=[1 0; 0 2]; EQ=[1 0; 0 2]; Measurement noise covariance Rh=0. 2; ER=0. 2; Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 33

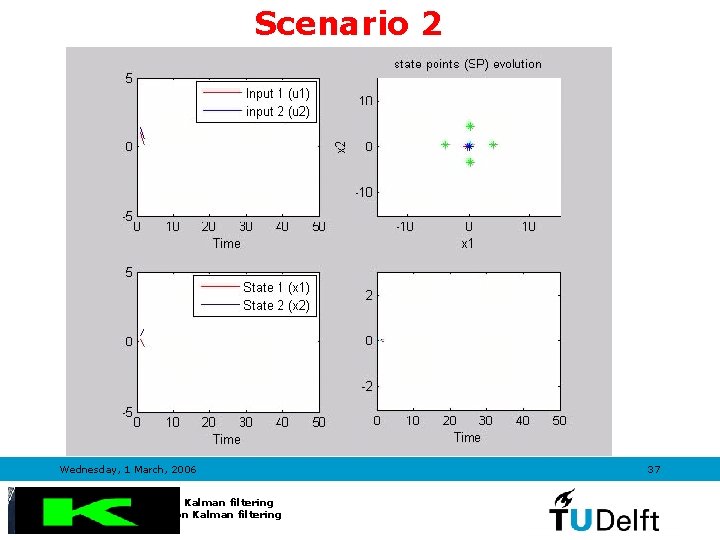
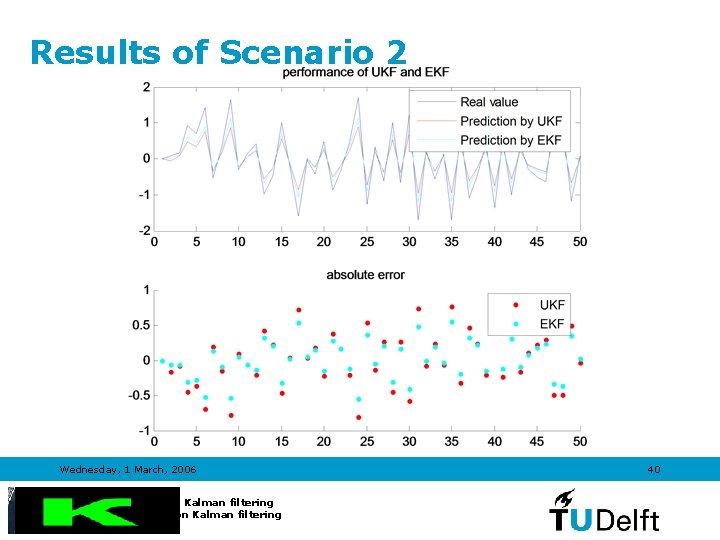
Scenario 2 • UKF • EKF Process noise covariance Qh=[10 0; 0 20]; EQ=[10 0; 0 20]; Measurement noise covariance Rh=0. 2; ER=0. 2; Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 34

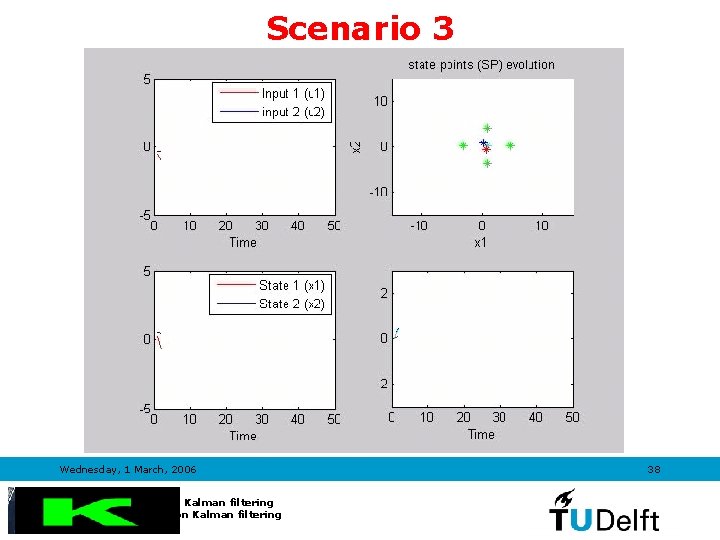
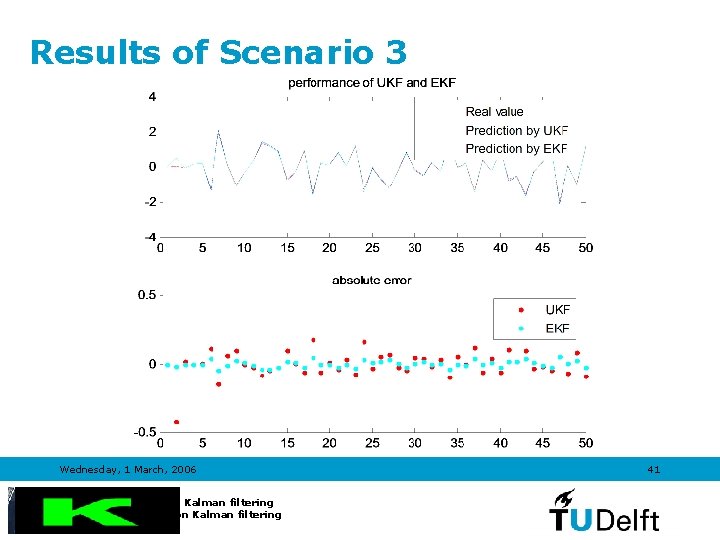
Scenario 3 • UKF • EKF Process noise covariance Qh=[100 0; 0 200]; EQ=[100 0; 0 200]; Measurement noise covariance Rh=0. 2; ER=0. 2; Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 35

Scenario 1 Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 36

Scenario 2 Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 37

Scenario 3 Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 38

Results of Scenario 1 Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 39

Results of Scenario 2 Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 40

Results of Scenario 3 Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 41

UKF Algorithm • State estimation • Parameter estimation • Dual UKF • An interesting topic • Questions for discussion Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 42

Step 1 of UKF for parameter estimation • Initialize with • Calculation of sigma points Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 43

Step 2 of UKF for parameter estimation • Weight outputs Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 44

Step 3 of UKF for parameter estimation • Weight covariance with respect to outputs • Weight covariance with respect to states and outputs Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 45

Step 4 of UKF for parameter estimation • Update state and state covariance Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 46

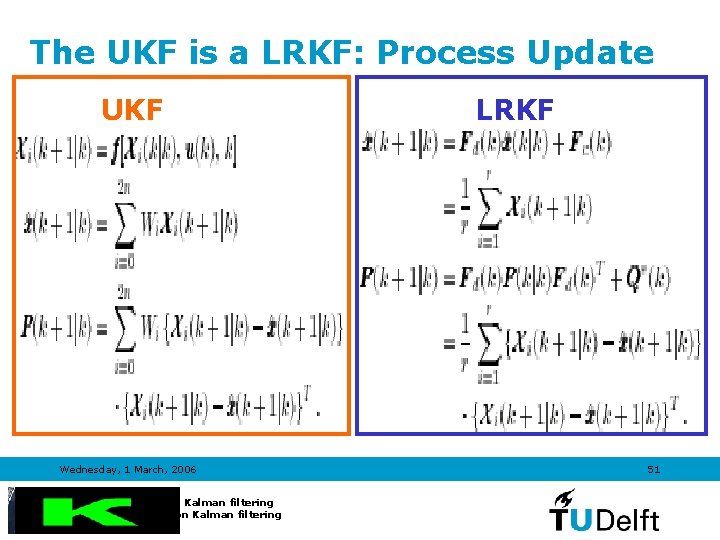
An interesting topic • UKF is a sort of Linear Regression Kalman Filter (LRKF) Tine Lefebvre, et al, Comment on “A New Method for the Nonlinear Transformation of Means and Covariances in Fitlers and Estimations”, IEEE Transactions on Automatic Control, Vol. 47, No, 8. August 2002 Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 47

Statistical Linear Regression of a Nonlinear Function Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 48

Statistical Linear Regression of a Nonlinear Function Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 49

Statistical Linear Regression of a Nonlinear Function Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 50

The UKF is a LRKF: Process Update UKF Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering LRKF 51

Proposed Adaptation to the UKF • The weights can be chosen as real numbers, the UKF then performs a weighted linear regression. • Sometimes, the UKF is used with k < 0 (resulting in negative weights) (see the aforementioned paper 1 and [1]). In this case, the calculated covariance matrices can be nonpositive, semidefinite. To overcome this problem, the covariances are artificially Increased Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 52

Questions for discussion The constant α determines the spread of the sigma points around , and is usually set to a small positive value. λ= α^2*(L+k)-L given k=3 -L β=2 0. 0001<α<1 then λ= α^2*(L+k)-L=a^2*3 -L Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 53

Weights 0. 00001^2*3 -L< λ<3 -L (L>3, negative) Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 54

Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 55

Questions for discussion How to guarantee the matrix square root? Positive Definite ? Wednesday, 1 March, 2006 Introduction to Kalman filtering TRAIL Course on Kalman filtering 56