The Unit Square 02 January 2022 6 a

The Unit Square 02 January 2022

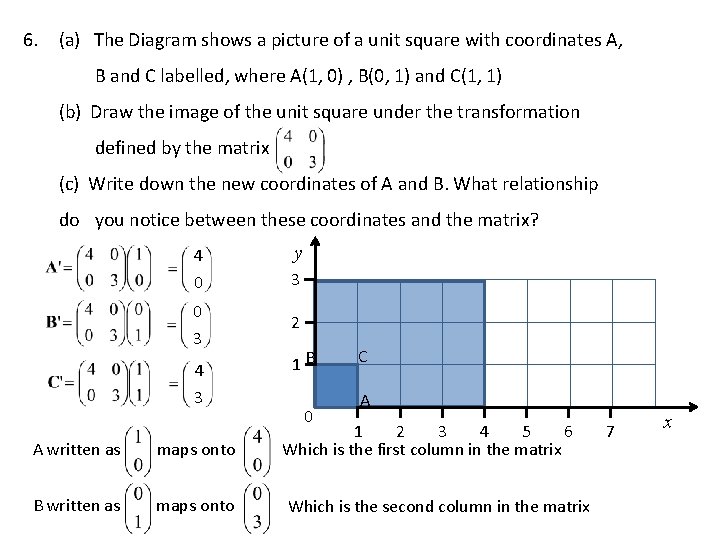
6. (a) The Diagram shows a picture of a unit square with coordinates A, B and C labelled, where A(1, 0) , B(0, 1) and C(1, 1) (b) Draw the image of the unit square under the transformation defined by the matrix (c) Write down the new coordinates of A and B. What relationship do you notice between these coordinates and the matrix? 4 0 0 3 4 3 A written as maps onto B written as maps onto y 3 2 1 B 0 C A 1 2 3 4 5 6 Which is the first column in the matrix Which is the second column in the matrix 7 x

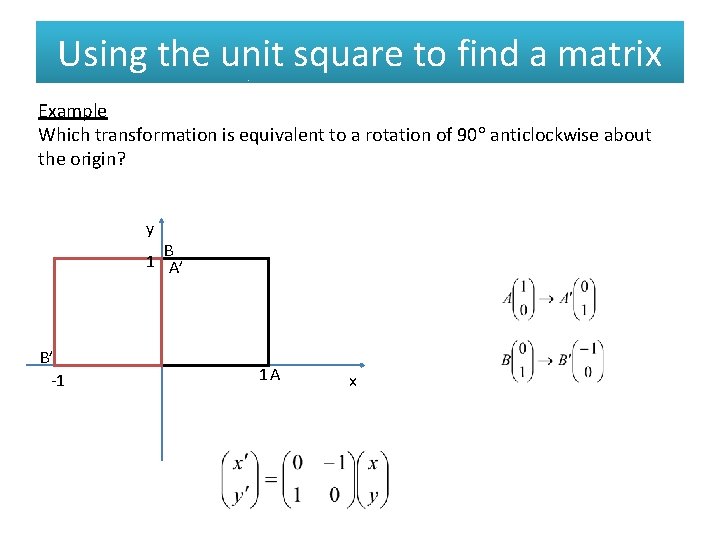
Using the unit square to find a matrix Example Which transformation is equivalent to a rotation of 90 anticlockwise about the origin? y B 1 A’ B’ -1 1 A x

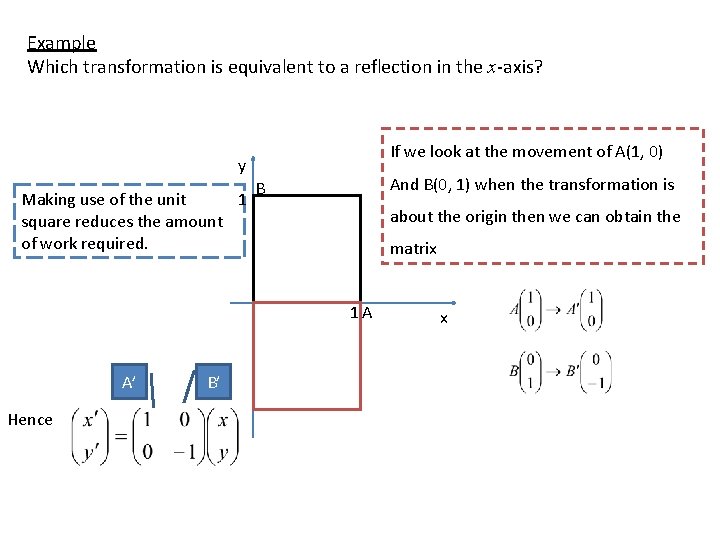
Example Which transformation is equivalent to a reflection in the x-axis? If we look at the movement of A(1, 0) y 1 Making use of the unit square reduces the amount of work required. And B(0, 1) when the transformation is B about the origin then we can obtain the matrix 1 A A’ Hence B’ x

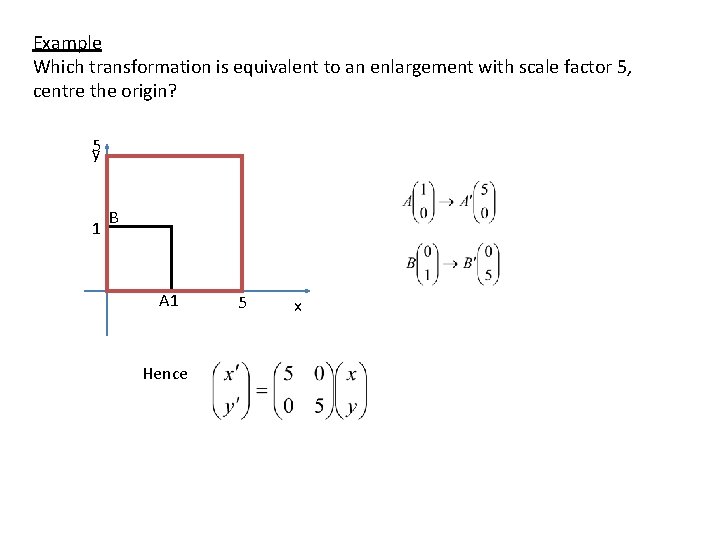
Example Which transformation is equivalent to an enlargement with scale factor 5, centre the origin? 5 y 1 B A 1 Hence 5 x

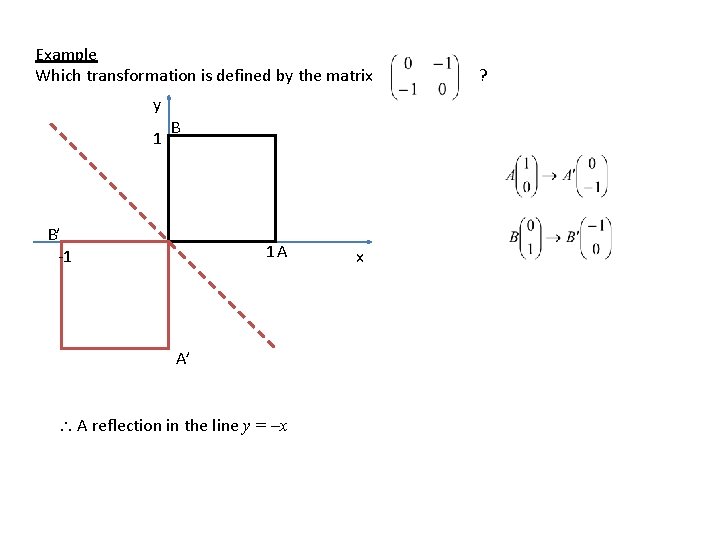
Example Which transformation is defined by the matrix y 1 B B’ -1 1 A A’ A reflection in the line y = –x x ?

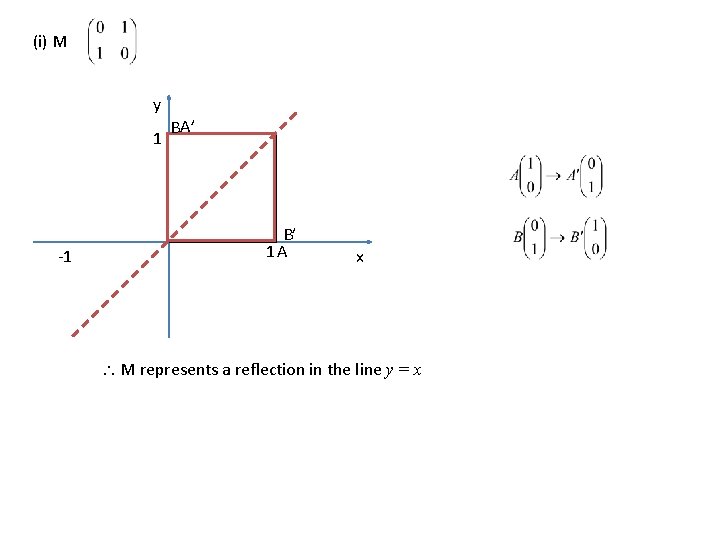
Combined Transformations Example If describe (i) M (ii) N (iii) MN and represent transformations M and N respectively,

(i) M y 1 -1 BA’ B’ 1 A x M represents a reflection in the line y = x

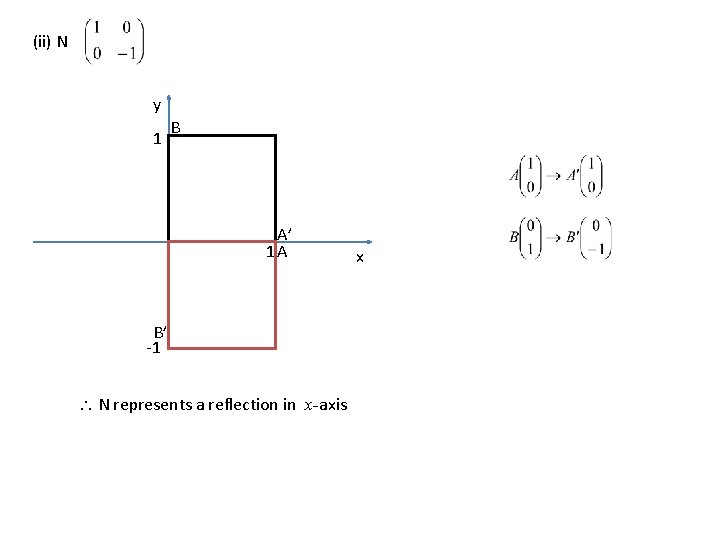
(ii) N y 1 B A’ 1 A B’ -1 N represents a reflection in x-axis x

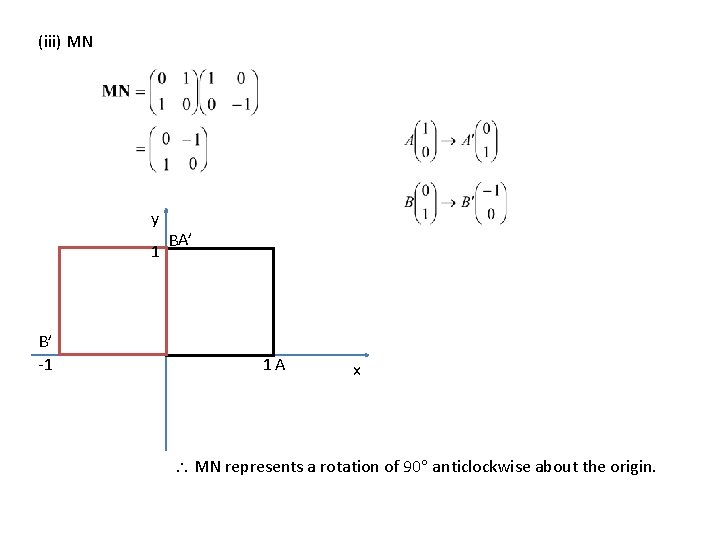
(iii) MN y 1 B’ -1 BA’ 1 A x MN represents a rotation of 90 anticlockwise about the origin.

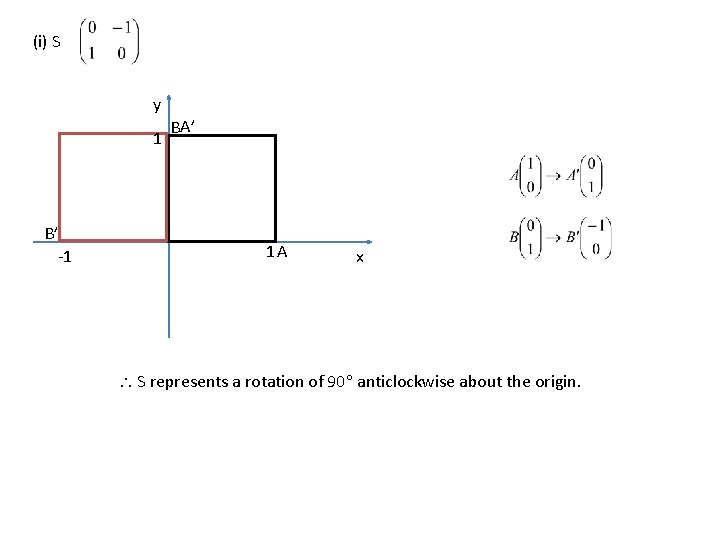
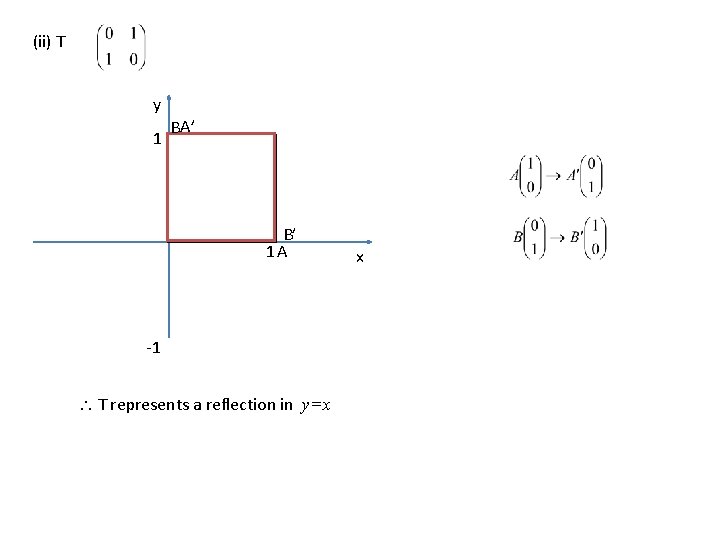
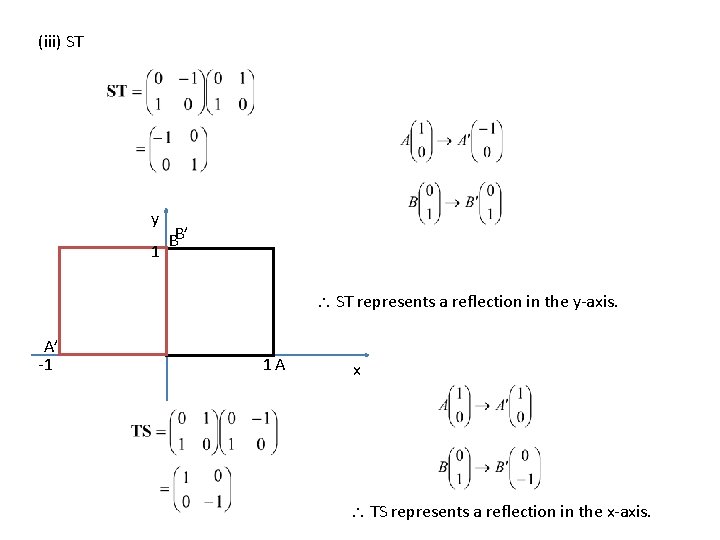
Example If and represent transformations S and T respectively, describe (i) S (ii) T (iii) ST (iv) Would TS give the same result?

(i) S y 1 B’ -1 BA’ 1 A x S represents a rotation of 90 anticlockwise about the origin.

(ii) T y 1 BA’ B’ 1 A -1 T represents a reflection in y=x x

(iii) ST y 1 BB’ ST represents a reflection in the y-axis. A’ -1 1 A x TS represents a reflection in the x-axis.

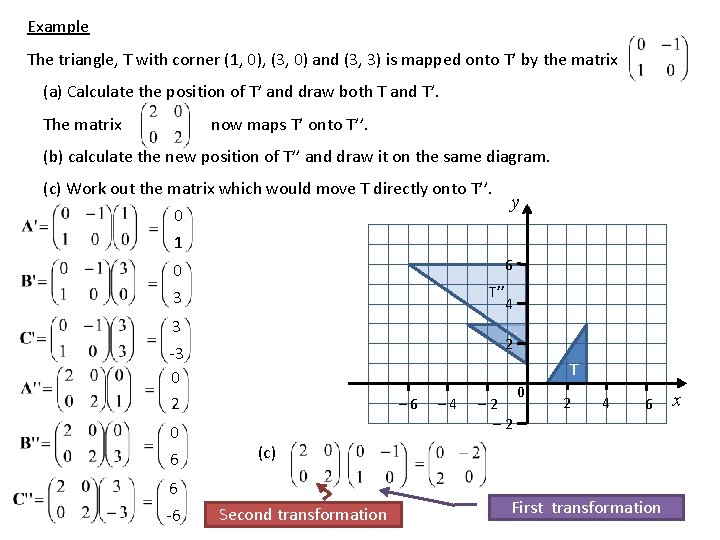
Example The triangle, T with corner (1, 0), (3, 0) and (3, 3) is mapped onto T’ by the matrix (a) Calculate the position of T’ and draw both T and T’. The matrix now maps T’ onto T’’. (b) calculate the new position of T’’ and draw it on the same diagram. (c) Work out the matrix which would move T directly onto T’’. 0 1 6 0 3 T’’ 3 -3 0 2 0 6 6 -6 y 4 2 T’ T – 6 – 4 – 2 0 2 4 6 (c) Second transformation First transformation x

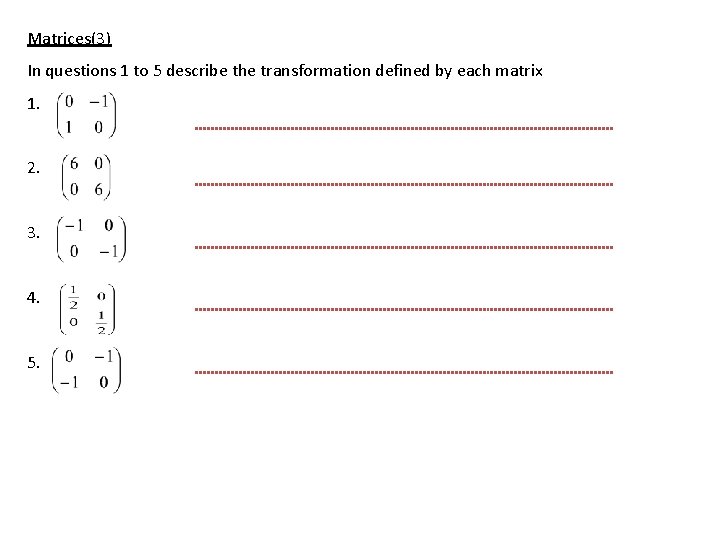
Matrices(3) In questions 1 to 5 describe the transformation defined by each matrix 1. 2. 3. 4. 5.

In questions 6 to 8 write down the 2 x 2 matrix being described 6. An enlargement, centre the origin and scale factor 2. 7. A rotation of 90 clockwise, centre the origin. 8. A reflection in the y-axis.

9. The rectangle, R with corner (2, 0), (4, 3) and (2, 3) is mapped onto R’ by the matrix (a) Calculate the position of R’ and draw both R and R’. The matrix now maps R’ onto R’’. (b) calculate the new position of R’’ and draw it on the same diagram. (c) describe fully the two transformations which have taken place. (d) Find the single transformation which will map R onto R’’ and its description.

10. M represents the transformation given by N represents the transformation given by The triangle T has vertices (0, 2) (4, 2) and (4, 3) (a) the triangle T is mapped onto T’ using matrix M. Draw on the same diagram T and the Image T’ (b) The triangle T’ is now mapped onto T’’ using matrix N. Draw the image of T’’ (c) Describe the transformations which have taken place. (d) Find the single transformation which will map T onto T’’ and its description.