The Unit Circle 2002 by R Villar All

The Unit Circle sin One of the most useful tools in trigonometry is the unit circle. It is a circle, with radius 1 unit, that is on the x-y coordinate plane. 1 cos The x-axis corresponds to the cosine function, and the y-axis corresponds to the sine function. The angles are measured from the positive x-axis (standard position) counterclockwise. In order to create the unit circle, we must use the special right triangles below: 1 45º 1 60º 30º -60º -90º The hypotenuse for each triangle is 1 unit. 45º -45º -90º

You first need to find the lengths of the other sides of each right triangle. . . 45º 1 1 30º 60º 45º

Now, use the corresponding triangle to find the coordinates on the unit circle. . . (0, 1) sin What are the coordinates of This cooresponds point? to (costhis 30, sin 30) (Use your (cos 30, sin 30) 30 -60 -90 triangle) 30º (– 1, 0) (0, – 1) cos (1, 0)

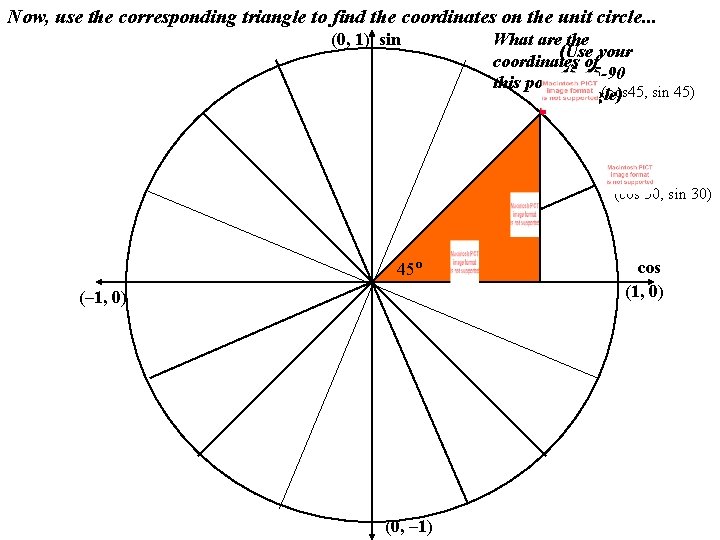
Now, use the corresponding triangle to find the coordinates on the unit circle. . . (0, 1) sin What are the (Use your coordinates of 45 -45 -90 this point? (cos 45, sin 45) triangle) (cos 30, sin 30) 45º (– 1, 0) (0, – 1) cos (1, 0)

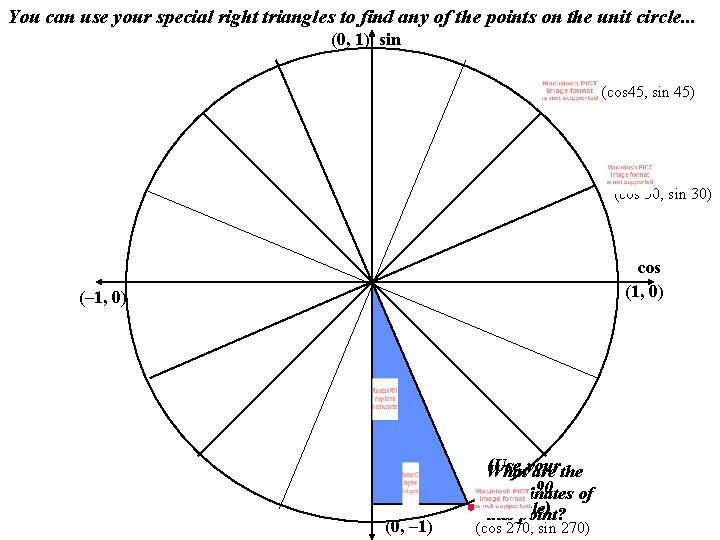
You can use your special right triangles to find any of the points on the unit circle. . . (0, 1) sin (cos 45, sin 45) (cos 30, sin 30) cos (1, 0) (– 1, 0) (0, – 1) (Use Whatyour are the 30 -60 -90 coordinates of triangle) this point? (cos 270, sin 270)

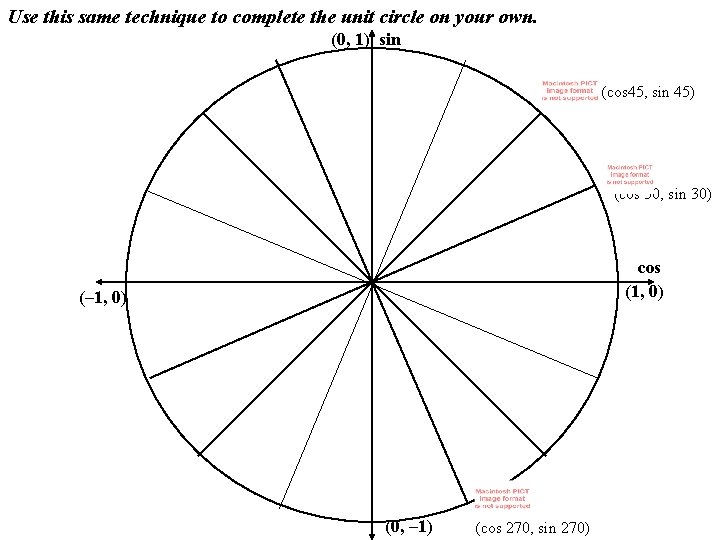
Use this same technique to complete the unit circle on your own. (0, 1) sin (cos 45, sin 45) (cos 30, sin 30) cos (1, 0) (– 1, 0) (0, – 1) (cos 270, sin 270)