The Tutte Polynomial Graph Polynomials 238900 winter 0506







































































- Slides: 78

The Tutte Polynomial Graph Polynomials 238900 winter 05/06

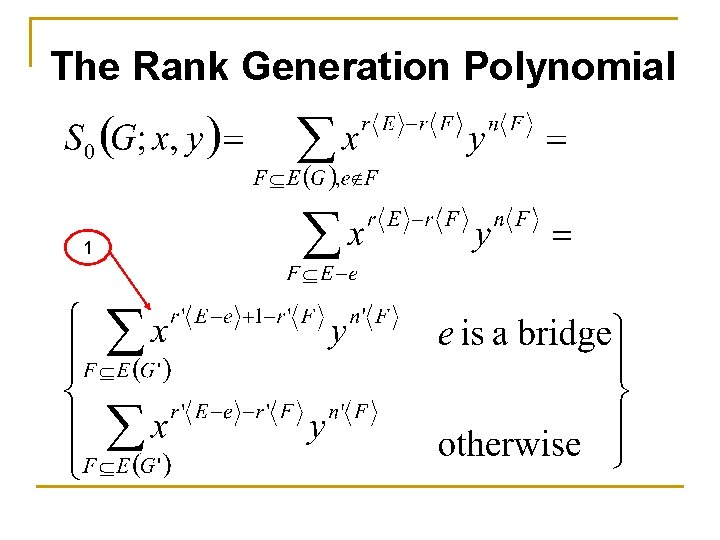
The Rank Generation Polynomial Reminder Number of connected components in G(V, F)

The Rank Generation Polynomial Theorem 2 In addition, S(En; x, y) = 1 for G(V, E) where |V|=n and |E|=0 Is the graph obtained by omitting edge e Is the graph obtained by contracting edge e

The Rank Generation Polynomial Theorem 2 – Proof Let us define : G’ = G’’ = G–e G/e r’<G> n’<G> r’’<G> n’’<G> r<G’> n<G’> r<G’’> n<G’’> = =

The Rank Generation Polynomial Theorem 2 – Proof Let us denote :

The Rank Generation Polynomial Observations

The Rank Generation Polynomial Observations

The Rank Generation Polynomial Observations

The Rank Generation Polynomial Observations 3

The Rank Generation Polynomial Observations 1 2

The Rank Generation Polynomial Reminder

The Rank Generation Polynomial Let us define

The Rank Generation Polynomial 1

The Rank Generation Polynomial

The Rank Generation Polynomial 3 2

The Rank Generation Polynomial

The Rank Generation Polynomial +

The Rank Generation Polynomial

The Rank Generation Polynomial Obvious

The Rank Generation Polynomial Obvious

The Rank Generation Polynomial

The Rank Generation Polynomial Obvious Q. E. D

The Tutte Polynomial

The Tutte Polynomial Reminder 4 5

The Universal Tutte Polynomial

The Universal Tutte Polynomial Theorem 6

The Universal Tutte Polynomial Theorem 6 - Proof 5

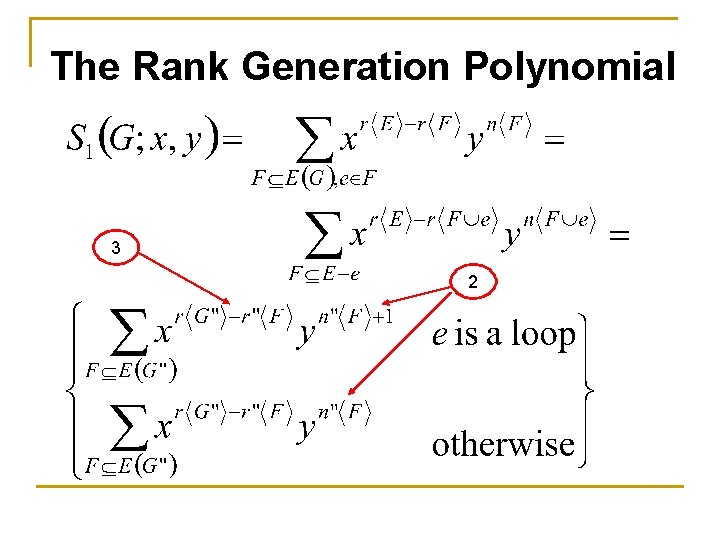
The Universal Tutte Polynomial If e is a bridge 4

The Universal Tutte Polynomial If e is a bridge

The Universal Tutte Polynomial If e is a loop 4

The Universal Tutte Polynomial If e is a bridge

The Universal Tutte Polynomial If e is neither a loop nor a bridge

The Universal Tutte Polynomial If e is neither a loop nor a bridge 4

The Universal Tutte Polynomial If e is neither a loop nor a bridge

The Universal Tutte Polynomial If e is neither a loop nor a bridge

The Universal Tutte Polynomial Theorem 6 - Proof Q. E. D

The Universal Tutte Polynomial Theorem 7 then

The Universal Tutte Polynomial Theorem 7 – proof V(G) is dependant entirely on V(G-e) and V(G/e). In addition – Q. E. D

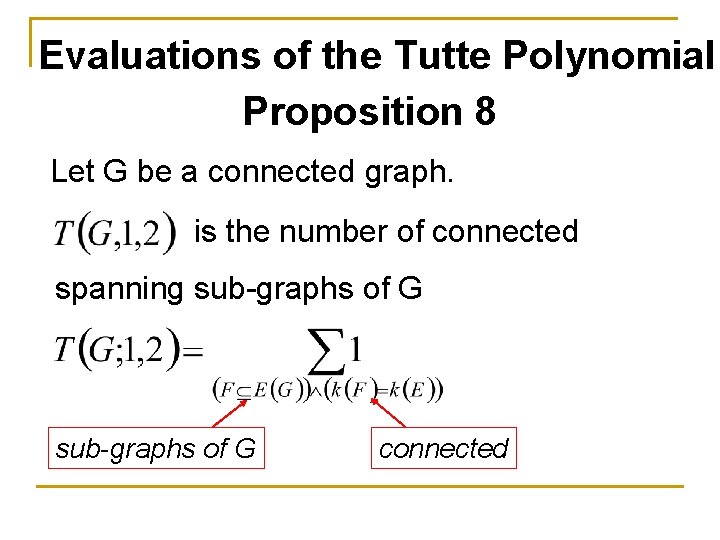
Evaluations of the Tutte Polynomial Proposition 8 Let G be a connected graph. is the number of spanning trees of G Shown in the previous lecture

Evaluations of the Tutte Polynomial Proposition 8 Let G be a connected graph. is the number of connected spanning sub-graphs of G

Evaluations of the Tutte Polynomial Proposition 8 Let G be a connected graph. is the number of connected spanning sub-graphs of G connected

Evaluations of the Tutte Polynomial Proposition 8 Let G be a connected graph. is the number of (edge sets forming) spanning forests of G Spanning forests

Evaluations of the Tutte Polynomial Proposition 8 Let G be a connected graph. is the number of spanning sub-graphs of G

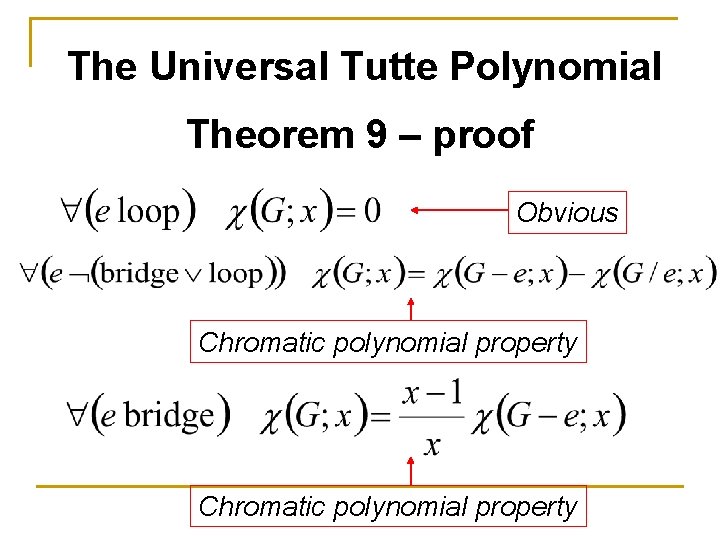
The Universal Tutte Polynomial Theorem 9 The chromatic polynomial and the Tutte polynomial are related by the equation :

The Universal Tutte Polynomial Theorem 9 – proof Claim :

The Universal Tutte Polynomial Theorem 9 – proof We must show that :

The Universal Tutte Polynomial Theorem 9 – proof and :

The Universal Tutte Polynomial Theorem 9 – proof Obvious. (empty graphs)

The Universal Tutte Polynomial Theorem 9 – proof Obvious Chromatic polynomial property

The Universal Tutte Polynomial Theorem 9 – proof Thus :

The Universal Tutte Polynomial Theorem 9 – proof And so, due to the uniqueness we shown in Theorem 7 :

The Universal Tutte Polynomial Theorem 9 – proof Remembering that :

The Universal Tutte Polynomial Theorem 9 – proof Remembering that : Q. E. D

Evaluations of the Tutte Polynomial Let G be a connected graph. is the number of acyclic orientations of G. We know that (Theorem 9) –

Evaluations of the Tutte Polynomial So – And thus –

Acyclic Orientations of Graphs Let G be a connected graph without loops or multiple edges. An orientation of a graph is received after assigning a direction to each edge. An orientation of a graph is acyclic if it does not contain any directed cycles.

Acyclic Orientations of Graphs Proposition 1. 1 is the number of pairs is a map where and is an orientation of G, subject to the following : • The orientation is acyclic •

Acyclic Orientations of Graphs Proof The secondition forces the map to be a proper coloring. The secondition is immediately implied from the first one.

Acyclic Orientations of Graphs Proof Conversely, if the map is proper, than the secondition defines a unique acyclic orientation of G. Hence, the number of allowed mappings is simply the number of proper coloring with x colors, which is by definition

Acyclic Orientations of Graphs be the number of pairs is a map where and is an orientation of G, subject to the following : • The orientation is acyclic •

Acyclic Orientations of Graphs Theorem 1. 2

Acyclic Orientations of Graphs Proof The chromatic polynomial is uniquely determined by the following : G 0 is the one vertex graph Disjoint union

Acyclic Orientations of Graphs Proof We now have to show for the new polynomial : Obvious G 0 is the one vertex graph Disjoint union Obvious

Acyclic Orientations of Graphs Proof We need to show that : Let :

Acyclic Orientations of Graphs Proof Let : Let be an acyclic orientation of G-e compatible with Let :

Acyclic Orientations of Graphs Proof Let be an orientation of G after adding {u v} to Let be an orientation of G after adding {v u} to

Acyclic Orientations of Graphs Proof We will show that for each pair exactly one of the orientations is acyclic and compatible with , expect for of them, in which case both are acyclic orientations compatible with

Acyclic Orientations of Graphs Proof Once this is done, we will know that – due to the definition of

Acyclic Orientations of Graphs Proof For each pair where - and is an acyclic orientation compatible with one of these three scenarios must hold :

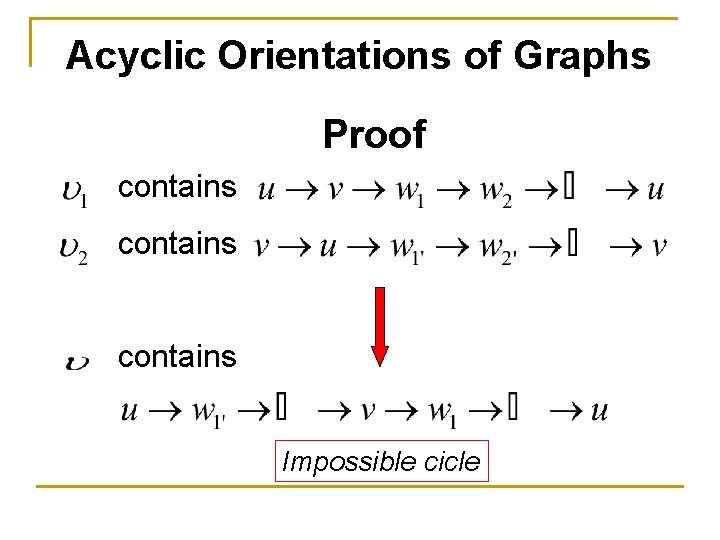
Acyclic Orientations of Graphs Proof Case 1 – Clearly is not compatible with while is compatible. Moreover, is acyclic : Impossible cicle

Acyclic Orientations of Graphs Proof Case 2 – Clearly is not compatible with while is compatible. Moreover, is acyclic : Impossible cicle

Acyclic Orientations of Graphs Proof Case 3 – Both are compatible with At least one is also acyclic. Suppose not, then: contains

Acyclic Orientations of Graphs Proof contains Impossible cicle

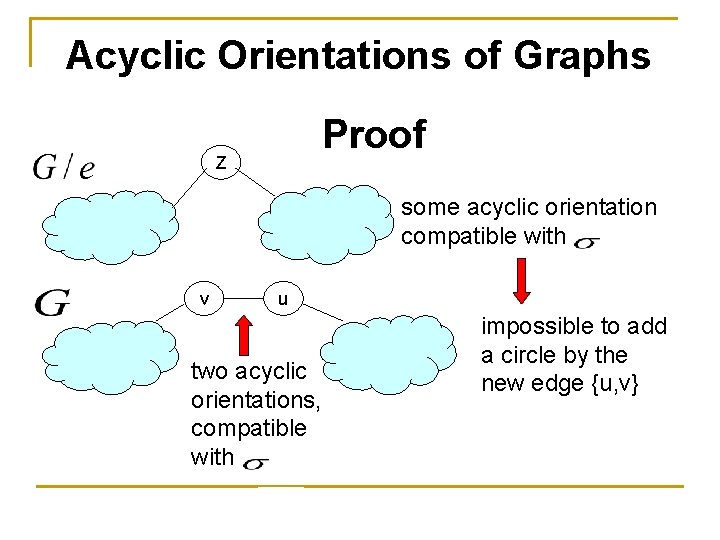
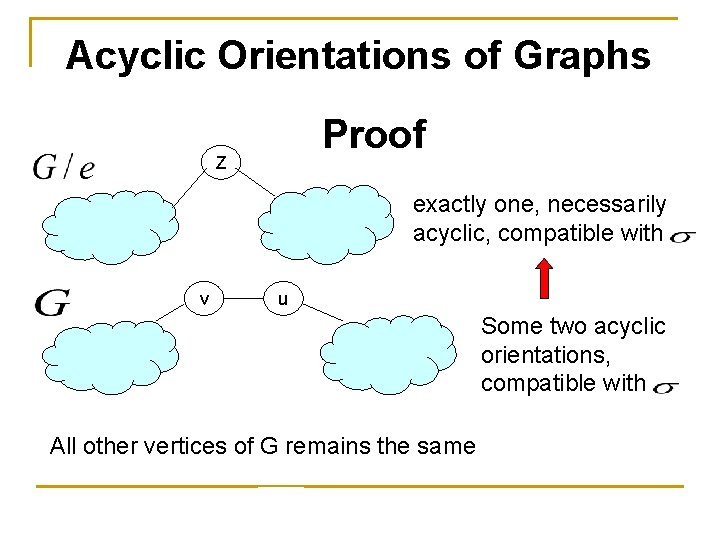
Acyclic Orientations of Graphs Proof We now have to show that both are acyclic for exactly with and pairs of Let z denote the vertex identifying {u, v} in

Acyclic Orientations of Graphs Proof Z some acyclic orientation compatible with v u two acyclic orientations, compatible with impossible to add a circle by the new edge {u, v}

Acyclic Orientations of Graphs Proof Z exactly one, necessarily acyclic, compatible with v u Some two acyclic orientations, compatible with All other vertices of G remains the same

Acyclic Orientations of Graphs Proof And so both exactly with And so – and are acyclic for pairs of

Acyclic Orientations of Graphs Proof It is obvious that for x = 1 every orientation is compatible with And so the expression count the number of acyclic orientations in G Q. E. D
 Permanent change of station regulation
Permanent change of station regulation Was ist deine lieblingsjahreszeit
Was ist deine lieblingsjahreszeit Winter kommt winter kommt flocken fallen nieder
Winter kommt winter kommt flocken fallen nieder Winter kommt flocken fallen nieder
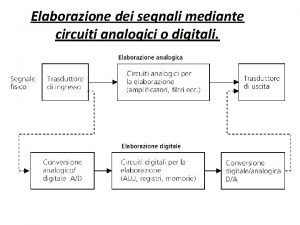
Winter kommt flocken fallen nieder Polynomial function table
Polynomial function table Review graphing polynomials
Review graphing polynomials Voi tutte opere del signore
Voi tutte opere del signore Porte logiche fondamentali
Porte logiche fondamentali Filastrocca nonsense
Filastrocca nonsense Cosa hanno in comune tutte le religioni
Cosa hanno in comune tutte le religioni La piccola circolazione
La piccola circolazione Nuvolette tutte d'oro
Nuvolette tutte d'oro Situazione economica schema
Situazione economica schema Voi tutte opere del signore
Voi tutte opere del signore Il chiasmo figura retorica
Il chiasmo figura retorica Tutte embedding
Tutte embedding Matplotlib inline
Matplotlib inline How to divide a polynomial by another polynomial
How to divide a polynomial by another polynomial What are the roots of a polynomial function
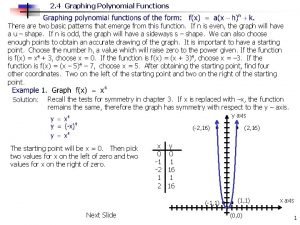
What are the roots of a polynomial function 4-4 graphing polynomial functions
4-4 graphing polynomial functions Polynomial time vs exponential time
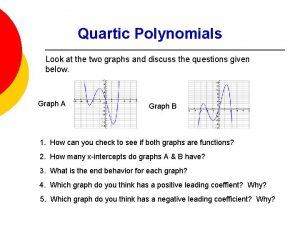
Polynomial time vs exponential time What does a quartic graph look like
What does a quartic graph look like Evaluate and graph polynomial functions
Evaluate and graph polynomial functions Degree and leading coefficient
Degree and leading coefficient Leading coefficient positive or negative
Leading coefficient positive or negative Transforming polynomial functions
Transforming polynomial functions A polynomial of the form y=ax2+bx+c is called
A polynomial of the form y=ax2+bx+c is called đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Cách giải mật thư tọa độ
Cách giải mật thư tọa độ Bổ thể
Bổ thể Tư thế worm breton
Tư thế worm breton ưu thế lai là gì
ưu thế lai là gì Thẻ vin
Thẻ vin Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Bàn tay mà dây bẩn
Bàn tay mà dây bẩn Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Diễn thế sinh thái là
Diễn thế sinh thái là Tư thế ngồi viết
Tư thế ngồi viết V. c c
V. c c Làm thế nào để 102-1=99
Làm thế nào để 102-1=99 Bài hát chúa yêu trần thế alleluia
Bài hát chúa yêu trần thế alleluia Sự nuôi và dạy con của hươu
Sự nuôi và dạy con của hươu đại từ thay thế
đại từ thay thế Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Công thức tiính động năng
Công thức tiính động năng Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Dot
Dot Lời thề hippocrates
Lời thề hippocrates Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Phản ứng thế ankan
Phản ứng thế ankan Các môn thể thao bắt đầu bằng tiếng chạy
Các môn thể thao bắt đầu bằng tiếng chạy Sự nuôi và dạy con của hổ
Sự nuôi và dạy con của hổ điện thế nghỉ
điện thế nghỉ Biện pháp chống mỏi cơ
Biện pháp chống mỏi cơ Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Frameset trong html5
Frameset trong html5 Gấu đi như thế nào
Gấu đi như thế nào Bảng số nguyên tố
Bảng số nguyên tố Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Tia chieu sa te
Tia chieu sa te Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Một số thể thơ truyền thống
Một số thể thơ truyền thống Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Hệ hô hấp
Hệ hô hấp Tư thế ngồi viết
Tư thế ngồi viết Resource allocation graph and wait for graph
Resource allocation graph and wait for graph Bridge graph
Bridge graph Scratchboard winter images
Scratchboard winter images Average temperature in rainforest
Average temperature in rainforest Map beyond the wall
Map beyond the wall Winter spring summer fall poem
Winter spring summer fall poem Mitoc winter school
Mitoc winter school Egc winter
Egc winter Rules for the weekend
Rules for the weekend Schneeballgedicht
Schneeballgedicht