THE THREE GREAT LAWS By Mark Theng 23

THE THREE GREAT LAWS By Mark Theng (23) Wang Shilin (25) Wong Chun Jie (26) Ernest Cheong (3)

Informative Introduction � � � The Three Great Laws apply to any triangle, not necessarily right-angled. Thus proving their greatness. We shall refer to the interior angles of any triangle as A, B and C. a, b and c refer to the sides opposite to angles A, B and C respectively. A b c C a B

The Great Law of Sines � � Also known as the Magnificent Sine Rule. The Great Law of Sine states categorically that for any triangle, a = b = c sin A sin B sin C

The Wonderful Proof a sin A = = a a/c c b sin B = = b b/c c

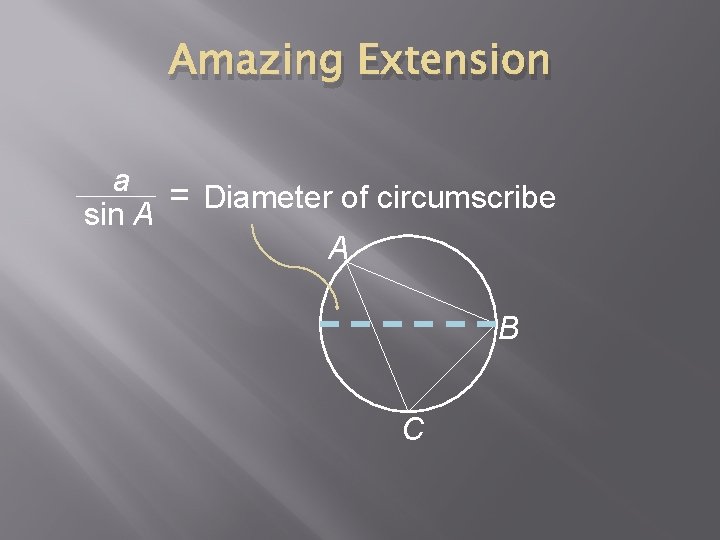
Amazing Extension a = Diameter of circumscribe sin A A B C

WHY? ? ? A B C c A b B a C a sin A = c = Diameter of circumscribe

The Great Law of Cosines � � Also known as the Magnificent Cosine Rule The Great Law of Cosines strongly enforces that all triangles conform to the statement: The Great Law of Cosines 2 c C = 2 a + 2 b – 2 ab cos

Fascinating Proof (Acute) c 2 = a 2 + b 2 – 2 ab cos C A b c 2 = a 2 + b 2 – 2 ab (n/b) c m c 2 = a 2 + b 2 – 2 an C B n a-n 2 2 2 c = (n + (a – n)) + b – 2 an a 2 2 c = n + 2 n(a – n) + b – 2 an c 2 = – n 2 + (a – n)2 + b 2 c 2 = (a – n)2 + m 2

Fascinating Proof (Obtuse) c 2 = a 2 + b 2 – 2 ab cos C A b c 2 = a 2 + b 2 – 2 ab (n/b) m c c 2 = a 2 + b 2 – 2 an C a B n-a c 2 = (n – a))2 + b 2 – 2 an n 2 2 c = n – 2 n(n – a) + b – 2 an c 2 = – n 2 + (n – a)2 + b 2 c 2 = (n – a)2 + m 2

The Great Law of Tangents � � Also known as the Magnificent Tangent Rule Ensures that for any shape fit to be a triangle: a – b = tan (A – B) / 2 a + b tan (A + B) / 2

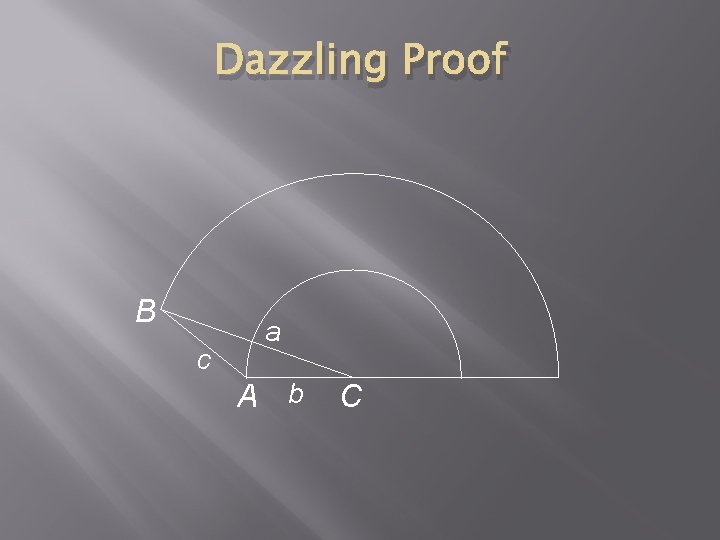
Dazzling Proof B c a A b C

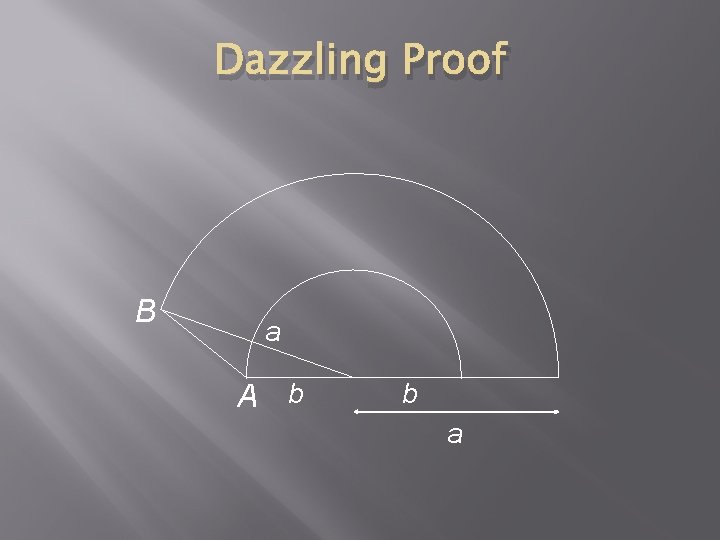
Dazzling Proof B a A b b a

Dazzling Proof B a– a b A b b b a a+b

Dazzling Proof B a– b A+B b a a+b

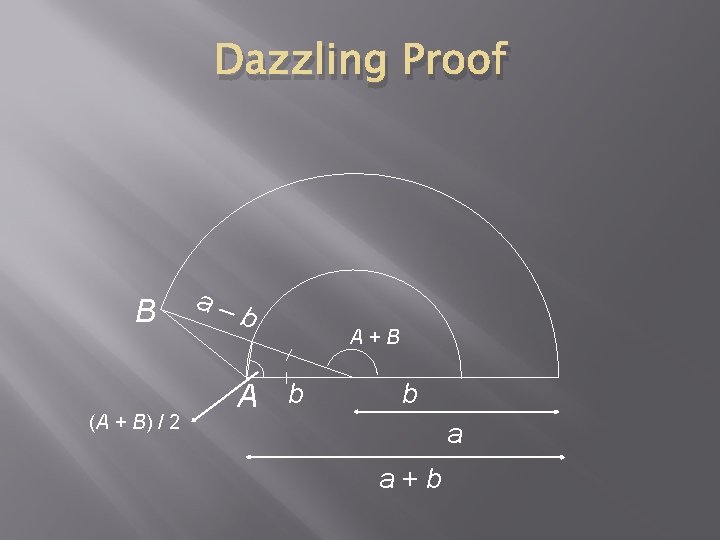
Dazzling Proof B (A + B) / 2 a– b A+B b a a+b

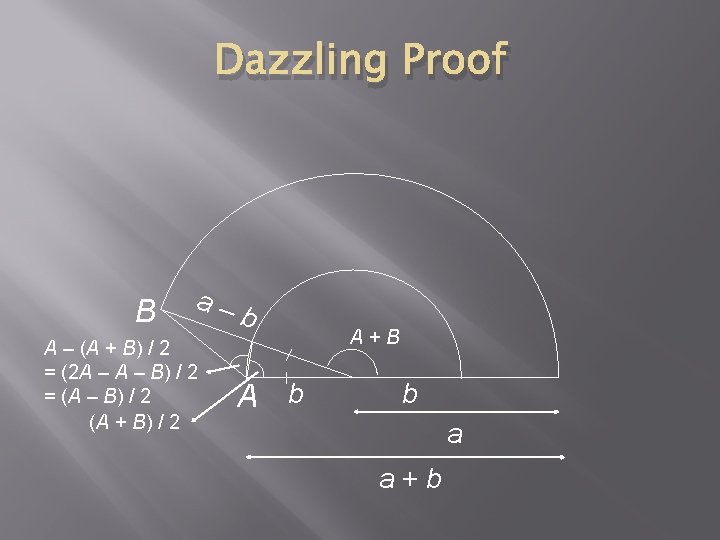
Dazzling Proof B a– A – (A + B) / 2 = (2 A – B) / 2 = (A – B) / 2 (A + B) / 2 b A+B b a a+b

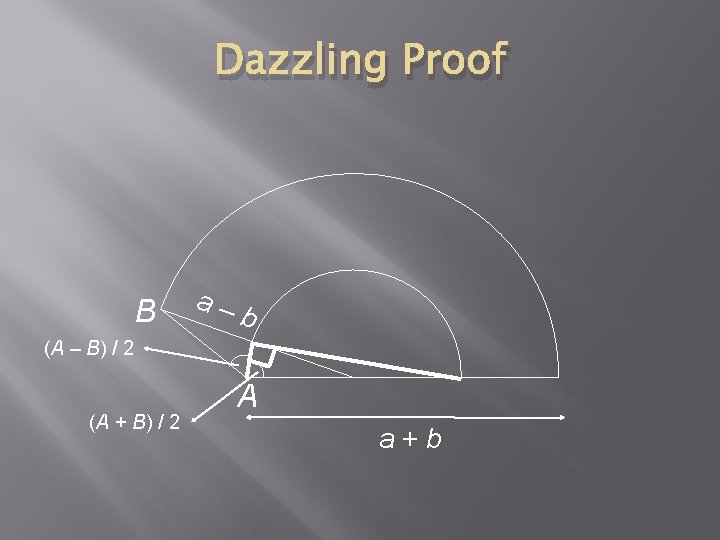
Dazzling Proof B a– b (A – B) / 2 (A + B) / 2 A a+b

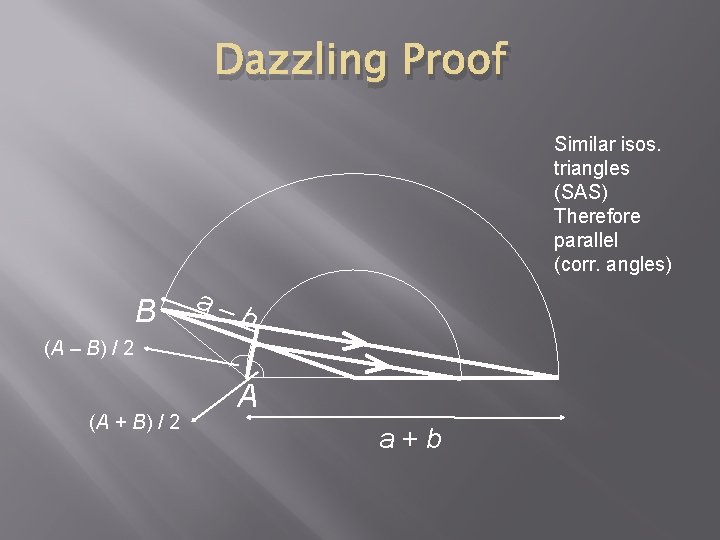
Dazzling Proof Similar isos. triangles (SAS) Therefore parallel (corr. angles) B a– b (A – B) / 2 (A + B) / 2 A a+b

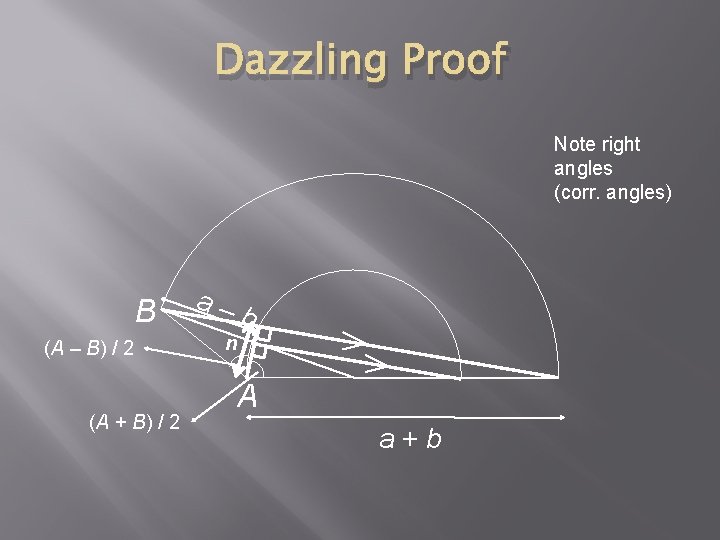
Dazzling Proof Note right angles (corr. angles) B (A – B) / 2 (A + B) / 2 a– b n A a+b

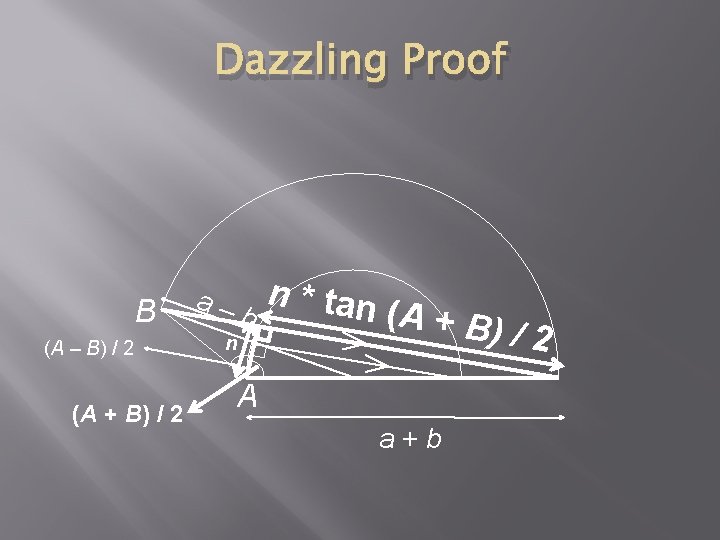
Dazzling Proof B (A – B) / 2 (A + B) / 2 a– b n n * tan (A + B )/2 A a+b

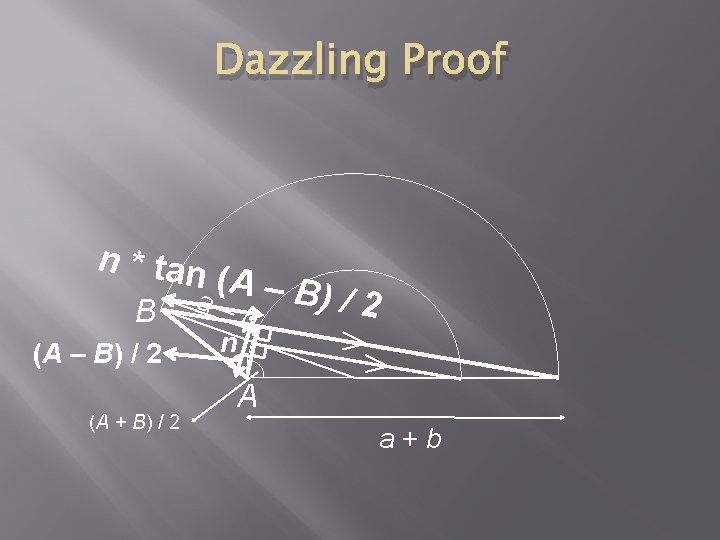
Dazzling Proof n * tan B (A – B) / 2 (A + B) / 2 ( A – B) a –b n /2 A a+b

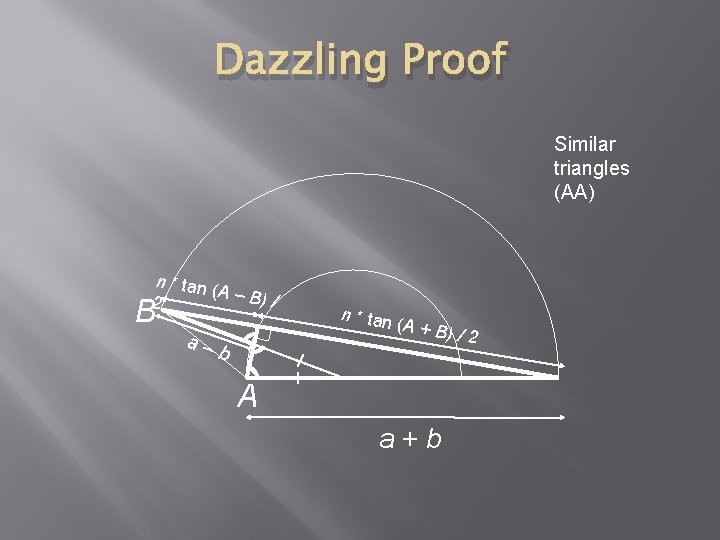
Dazzling Proof Similar triangles (AA) n * tan (A – B) / 2 B a– b n * tan (A + B) A a+b /2

Dazzling Proof n * tan (A – B) / 2 B a– b n * tan (A + B) /2 A a+b = a–b n * tan (A + B) / 2 n * tan (A – B) / 2

WE DID IT!!! a+b a–b = tan (A + B) / 2 tan (A – B) / 2

THANK YOU!!! Any thought provoking questions?

Respectable Sources � � http: //wlym. com/~animations/lawoftangents. htm l http: //www. wikipedia. org/