The The Unit Circle Warm Up Lesson Presentation

The The. Unit. Circle Warm Up Lesson Presentation Lesson Quiz Holt. Mc. Dougal Algebra 2 Holt

The Unit Circle Warm Up Find the measure of the reference angle for each given angle. 1. 120° 60° 2. 225° 45° 3. – 150° 30° 4. 315° 45° Find the exact value of each trigonometric function. 5. sin 60° 6. tan 45° 7. cos 45° 8. cos 60° Holt Mc. Dougal Algebra 2 1

The Unit Circle Objectives Convert angle measures between degrees and radians. Find the values of trigonometric functions on the unit circle. Holt Mc. Dougal Algebra 2

The Unit Circle Vocabulary radian unit circle Holt Mc. Dougal Algebra 2

The Unit Circle So far, you have measured angles in degrees. You can also measure angles in radians. A radian is a unit of angle measure based on arc length. Recall from geometry that an arc is an unbroken part of a circle. If a central angle θ in a circle of radius r, then the measure of θ is defined as 1 radian. Holt Mc. Dougal Algebra 2

The Unit Circle The circumference of a circle of radius r is 2 r. Therefore, an angle representing one complete clockwise rotation measures 2 radians. You can use the fact that 2 radians is equivalent to 360° to convert between radians and degrees. Holt Mc. Dougal Algebra 2

The Unit Circle Holt Mc. Dougal Algebra 2

The Unit Circle Example 1: Converting Between Degrees and Radians Convert each measure from degrees to radians or from radians to degrees. A. – 60° . B. Holt Mc. Dougal Algebra 2

The Unit Circle Reading Math Angles measured in radians are often not labeled with the unit. If an angle measure does not have a degree symbol, you can usually assume that the angle is measured in radians. Holt Mc. Dougal Algebra 2

The Unit Circle Check It Out! Example 1 Convert each measure from degrees to radians or from radians to degrees. a. 80° 4 9 . b. 20. Holt Mc. Dougal Algebra 2

The Unit Circle Check It Out! Example 1 Convert each measure from degrees to radians or from radians to degrees. c. – 36° 5. d. 4 radians . Holt Mc. Dougal Algebra 2

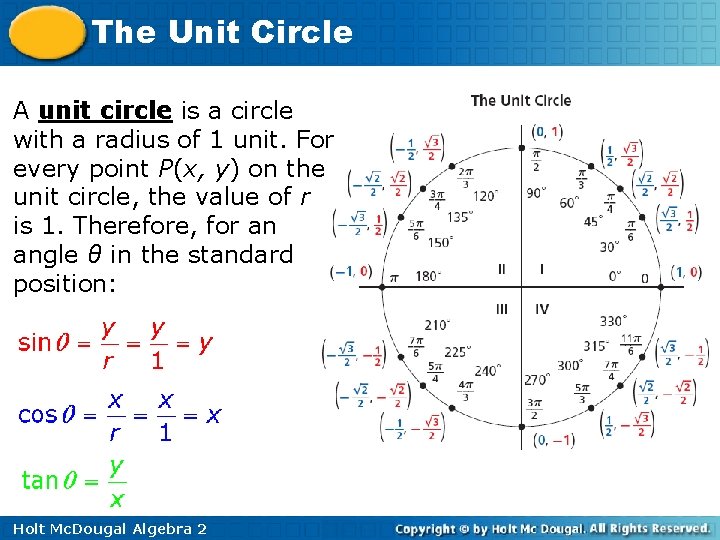
The Unit Circle A unit circle is a circle with a radius of 1 unit. For every point P(x, y) on the unit circle, the value of r is 1. Therefore, for an angle θ in the standard position: Holt Mc. Dougal Algebra 2

The Unit Circle So the coordinates of P can be written as (cosθ, sinθ). The diagram shows the equivalent degree and radian measure of special angles, as well as the corresponding xand y-coordinates of points on the unit circle. Holt Mc. Dougal Algebra 2

The Unit Circle Example 2 A: Using the Unit Circle to Evaluate Trigonometric Functions Use the unit circle to find the exact value of each trigonometric function. cos 225° The angle passes through the point on the unit circle. cos 225° = x Holt Mc. Dougal Algebra 2 Use cos θ = x.

The Unit Circle Example 2 B: Using the Unit Circle to Evaluate Trigonometric Functions Use the unit circle to find the exact value of each trigonometric function. tan The angle passes through the point on the unit circle. Use tan θ = Holt Mc. Dougal Algebra 2 .

The Unit Circle Check It Out! Example 1 a Use the unit circle to find the exact value of each trigonometric function. sin 315° The angle passes through the point on the unit circle. sin 315° = y Holt Mc. Dougal Algebra 2 Use sin θ = y.

The Unit Circle Check It Out! Example 1 b Use the unit circle to find the exact value of each trigonometric function. tan 180° The angle passes through the point (– 1, 0) on the unit circle. tan 180° = Holt Mc. Dougal Algebra 2 Use tan θ = .

The Unit Circle Check It Out! Example 1 c Use the unit circle to find the exact value of each trigonometric function. The angle passes through the point on the unit circle. Holt Mc. Dougal Algebra 2

The Unit Circle You can use reference angles and Quadrant I of the unit circle to determine the values of trigonometric functions. Trigonometric Functions and Reference Angles Holt Mc. Dougal Algebra 2

The Unit Circle The diagram shows how the signs of the trigonometric functions depend on the quadrant containing the terminal side of θ in standard position. Holt Mc. Dougal Algebra 2

The Unit Circle Example 3: Using Reference Angles to Evaluate Trigonometric functions Use a reference angle to find the exact value of the sine, cosine, and tangent of 330°. Step 1 Find the measure of the reference angle. The reference angle measures 30° Holt Mc. Dougal Algebra 2

The Unit Circle Example 3 Continued Step 2 Find the sine, cosine, and tangent of the reference angle. Use sin θ = y. Use cos θ = x. Holt Mc. Dougal Algebra 2

The Unit Circle Example 3 Continued Step 3 Adjust the signs, if needed. In Quadrant IV, sin θ is negative. In Quadrant IV, cos θ is positive. In Quadrant IV, tan θ is negative. Holt Mc. Dougal Algebra 2

The Unit Circle Check It Out! Example 3 a Use a reference angle to find the exact value of the sine, cosine, and tangent of 270°. Step 1 Find the measure of the reference angle. The reference angle measures 90° Holt Mc. Dougal Algebra 2 270°

The Unit Circle Check It Out! Example 3 a Continued Step 2 Find the sine, cosine, and tangent of the reference angle. sin 90° = 1 Use sin θ = y. 90° cos 90° = 0 tan 90° = undef. Holt Mc. Dougal Algebra 2 Use cos θ = x.

The Unit Circle Check It Out! Example 3 a Continued Step 3 Adjust the signs, if needed. sin 270° = – 1 cos 270° = 0 tan 270° = undef. Holt Mc. Dougal Algebra 2 In Quadrant IV, sin θ is negative.

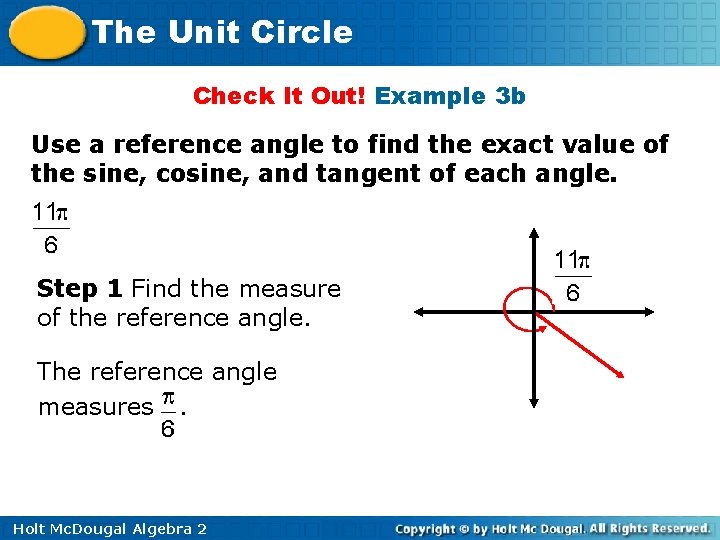
The Unit Circle Check It Out! Example 3 b Use a reference angle to find the exact value of the sine, cosine, and tangent of each angle. Step 1 Find the measure of the reference angle. The reference angle measures. Holt Mc. Dougal Algebra 2

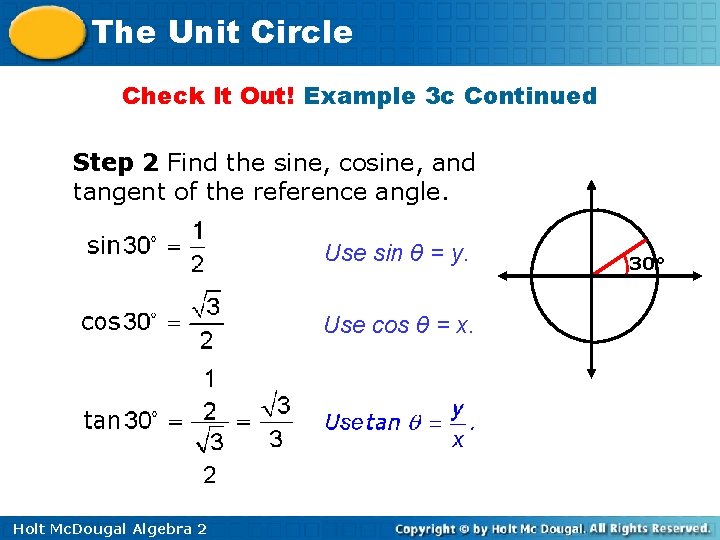
The Unit Circle Check It Out! Example 3 b Continued Step 2 Find the sine, cosine, and tangent of the reference angle. Use sin θ = y. Use cos θ = x. Holt Mc. Dougal Algebra 2 30°

The Unit Circle Check It Out! Example 3 b Continued Step 3 Adjust the signs, if needed. In Quadrant IV, sin θ is negative. In Quadrant IV, cos θ is positive. In Quadrant IV, tan θ is negative. Holt Mc. Dougal Algebra 2

The Unit Circle Check It Out! Example 3 c Use a reference angle to find the exact value of the sine, cosine, and tangent of each angle. – 30° Step 1 Find the measure of the reference angle. The reference angle measures 30°. Holt Mc. Dougal Algebra 2 – 30°

The Unit Circle Check It Out! Example 3 c Continued Step 2 Find the sine, cosine, and tangent of the reference angle. Use sin θ = y. Use cos θ = x. Holt Mc. Dougal Algebra 2 30°

The Unit Circle Check It Out! Example 3 c Continued Step 3 Adjust the signs, if needed. In Quadrant IV, sin θ is negative. In Quadrant IV, cos θ is positive. In Quadrant IV, tan θ is negative. Holt Mc. Dougal Algebra 2

The Unit Circle If you know the measure of a central angle of a circle, you can determine the length s of the arc intercepted by the angle. Holt Mc. Dougal Algebra 2

The Unit Circle Holt Mc. Dougal Algebra 2

The Unit Circle Example 4: Automobile Application A tire of a car makes 653 complete rotations in 1 min. The diameter of the tire is 0. 65 m. To the nearest meter, how far does the car travel in 1 s? Step 1 Find the radius of the tire. The radius is diameter. of the Step 2 Find the angle θ through which the tire rotates in 1 second. Write a proportion. Holt Mc. Dougal Algebra 2

The Unit Circle Example 4 Continued The tire rotates θ radians in 1 s and 653(2 ) radians in 60 s. Cross multiply. Divide both sides by 60. Simplify. Holt Mc. Dougal Algebra 2

The Unit Circle Example 4 Continued Step 3 Find the length of the arc intercepted by radians. Use the arc length formula. Substitute 0. 325 for r and for θ Simplify by using a calculator. The car travels about 22 meters in second. Holt Mc. Dougal Algebra 2

The Unit Circle Check It Out! Example 4 An minute hand on Big Ben’s Clock Tower in London is 14 ft long. To the nearest tenth of a foot, how far does the tip of the minute hand travel in 1 minute? Step 1 Find the radius of the clock. The radius is the actual r =14 length of the hour hand. Step 2 Find the angle θ through which the hour hand rotates in 1 minute. Write a proportion. Holt Mc. Dougal Algebra 2

The Unit Circle Check It Out! Example 4 Continued The hand rotates θ radians in 1 m and 2 radians in 60 m. Cross multiply. Divide both sides by 60. Simplify. Holt Mc. Dougal Algebra 2

The Unit Circle Check It Out! Example 4 Continued Step 3 Find the length of the arc intercepted by radians. Use the arc length formula. s ≈ 1. 5 feet Substitute 14 for r and for θ. Simplify by using a calculator. The minute hand travels about 1. 5 feet in one minute. Holt Mc. Dougal Algebra 2

The Unit Circle Lesson Quiz: Part I Convert each measure from degrees to radians or from radians to degrees. 1. 100° 2. 144° 3. Use the unit circle to find the exact value of 4. Use a reference angle to find the exact value of the sine, cosine, and tangent of Holt Mc. Dougal Algebra 2 .

The Unit Circle Lesson Quiz: Part II 5. A carpenter is designing a curved piece of molding for the ceiling of a museum. The curve will be an arc of a circle with a radius of 3 m. The central angle will measure 120°. To the nearest tenth of a meter, what will be the length of the molding? 6. 3 m Holt Mc. Dougal Algebra 2