The substitution rule for definite integrals If g

![The substitution rule for definite integrals If g’ is continuous on [a, b], and The substitution rule for definite integrals If g’ is continuous on [a, b], and](http://slidetodoc.com/presentation_image_h2/475e759140c0ea7afb15dd7f75d06a33/image-2.jpg)
The substitution rule for definite integrals If g’ is continuous on [a, b], and f is continuous on the range of u=g(x) then

The substitution rule for definite integrals Example 1 e The area of the yellow domain is ½.

Definite Integrals by Substitution 1) Choose u. 2) Calculate du. 3) Calculate dx 4) Do a straight replacement A. Substitute in u. Arrange to have du in your integral also. B. Substitute in dx (All xs and dxs must be replaced!) (All xs and dxs must be eliminated!) 5) Solve the new integral. 6) Evaluating using u - Change the limits of integration from [a, b] to [u(a), u(b)] 6) Evaluating using x - Substitute back in to get x again. No need to change limits of integration.

Example new limit Find new limits

Example Don’t forget to use the new limits.

Integrals of Even and Odd Functions Theorem

Integrals of Even and Odd Functions Problem Solution An odd function is symmetric with respect to the origin. The definite integral from -a to a, in the case of the function shown in this picture, is the area of the blue domain minus the area of the red domain. By symmetry these areas are equal, hence the integral is 0. -a a

Bell Ringer Given: Write a similar expression for the continuous function:


Indefinite Integral of x -1 • The rule is • Try it out … 11

Verify the antidervative formulas • 12


The Substitution Rule • If u=g(x) is differentiable function whose range is an interval I, and f is continuous on I, then • The Substitution rule is proved using the Chain Rule for differentiation. • The idea behind the substitution rule is to replace a relatively complicated integral by a simpler integral. This is accomplished by changing from the original variable x to a new variable u that is a function of x. • The main challenge is to think of an appropriate substitution.

Example The variable of integration must match the variable in the expression. Don’t forget to substitute the value for u back into the problem!

The same substitution holds for the higher power! • With • Back to x (Indefinite):

Substitution rule examples Example We computed du by straightforward differentiation of the expression for u. The substitution u = 2 x was suggested by the function to be integrated. The main problem in integrating by substitution is to find the right substitution which simplifies the integral so that it can be computed by the table of basic integrals.

Choosing u • Try to choose u to be an inside function. (Think chain rule. ) • Try to choose u so that du is in the problem, except for a constant multiple. For our example u = 3 x + 2 was a good choice because (1) 3 x + 2 is inside the exponential. (2) The derivative is 3, which is only a constant.

Example A linear substitution: Let u = 3 x + 2. Then du = 3 dx.

Example about choosing the substitution Example Solution This rewriting allows us to finish the computation using basic formulae. Next substitute back to the original variable.

Using the Chain Rule, we know that: Evaluate:

Using the Chain Rule, we know that: Evaluate: Looks almost like cos(x 2) 2 x, which is the derivative of sin(x 2). We will rearrange the integral to get an exact match:

Using the Chain Rule, we know that: Evaluate: We will rearrange the integral to get an exact match:

Using the Chain Rule, we know that: Evaluate: We will rearrange the integral to get an exact match:

Using the Chain Rule, we know that: Evaluate: We will rearrange the integral to get an exact match: We put in a 2 so the pattern will match.

Using the Chain Rule, we know that: Evaluate: We will rearrange the integral to get an exact match: We put in a 2 so the pattern will match. So we must also put in a 1/2 to keep the problem the same.

Using the Chain Rule, we know that: Evaluate: We will rearrange the integral to get an exact match:

Using the Chain Rule, we know that: Evaluate: We will rearrange the integral to get an exact match:

Check Answer:

Check Answer: Check:

Check Answer: Check: From the chain rule

Practice Let u = du =

Practice Let u = x 2 + 1 du =

Practice Let u = x 2 + 1 du = 2 x dx

Practice Let u = x 2 + 1 du = 2 x dx
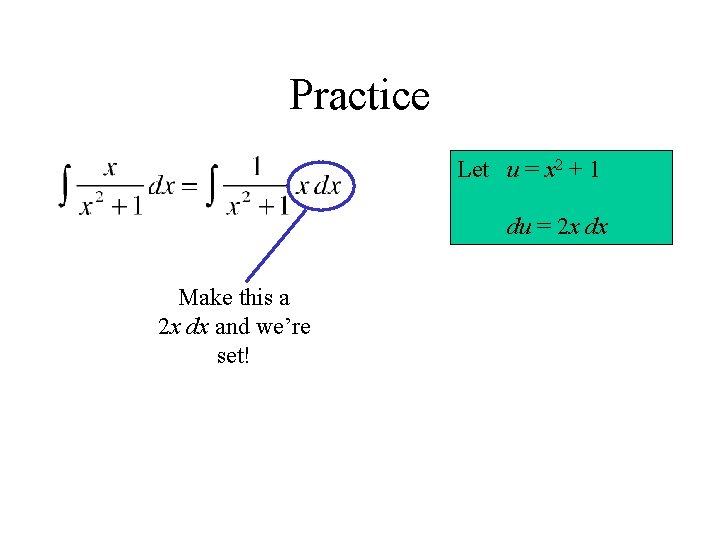
Practice Let u = x 2 + 1 du = 2 x dx Make this a 2 x dx and we’re set!

Practice Let u = x 2 + 1 du = 2 x dx
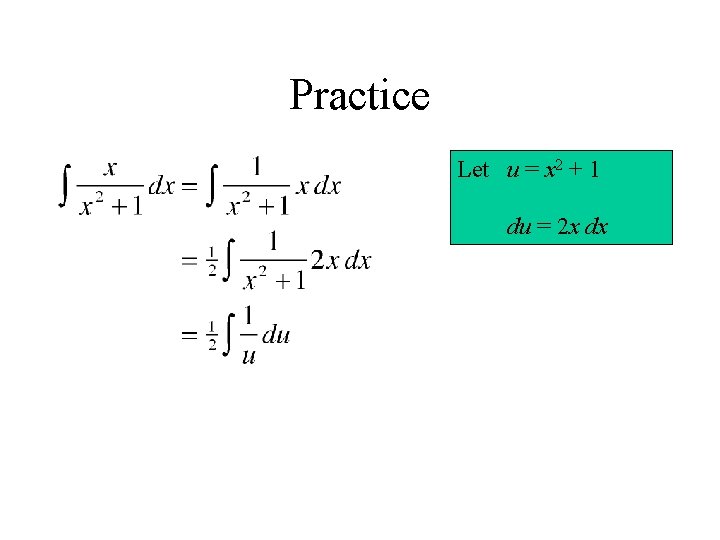
Practice Let u = x 2 + 1 du = 2 x dx

Practice Let u = x 2 + 1 du = 2 x dx

Practice Let u = x 2 + 1 du = 2 x dx

Practice Let u = du =

Practice Let u = sin(x) du =

Practice Let u = sin(x) du = cos(x) dx

Practice Let u = sin(x) du = cos(x) dx

Practice Let u = sin(x) du = cos(x) dx

Practice Let u = sin(x) du = cos(x) dx

Practice An alternate possibility: Let u = du =

Practice An alternate possibility: Let u = cos(x) du = –sin(x) dx

Practice An alternate possibility: Let u = cos(x) du = –sin(x) dx

Practice An alternate possibility: Let u = cos(x) du = –sin(x) dx

Practice An alternate possibility: Let u = cos(x) du = –sin(x) dx

Practice Note:

Practice Note:

Practice Note: What’s the difference?

Practice Note: What’s the difference?

Practice Note: What’s the difference?

Practice Note: What’s the difference? This is 1!

Practice Note: What’s the difference?

Practice Note: What’s the difference? That is, the difference is a constant.

Practice Note: What’s the difference? That is, the difference is a constant.

In-Class Assignment • Integrate using two different methods: – 1 st by multiplying out and integrating – 2 nd by u-substitution Do you get the same result? (Don’t just assume or claim you do; multiply out your results to show it!) If you don’t get exactly the same answer, is it a problem? Why or why not?

Integrals of Even and Odd Functions Theorem

Integrals of Even and Odd Functions Problem Solution An odd function is symmetric with respect to the origin. The definite integral from -a to a, in the case of the function shown in this picture, is the area of the blue domain minus the area of the red domain. By symmetry these areas are equal, hence the integral is 0. -a a

The substitution rule for definite integrals Example 1 e The area of the yellow domain is ½.

Example new limit Find new limits

Example Don’t forget to use the new limits.
![The substitution rule for definite integrals If g’ is continuous on [a, b], and The substitution rule for definite integrals If g’ is continuous on [a, b], and](http://slidetodoc.com/presentation_image_h2/475e759140c0ea7afb15dd7f75d06a33/image-67.jpg)
The substitution rule for definite integrals If g’ is continuous on [a, b], and f is continuous on the range of u=g(x) then

Indefinite Integrals by Substitution 1) Choose u.

Indefinite Integrals by Substitution 1) Choose u. 2) Calculate du.

Indefinite Integrals by Substitution 1) Choose u. 2) Calculate du. 3) Substitute u. Arrange to have du in your integral also. (All xs and dxs must be replaced!)

Indefinite Integrals by Substitution 1) Choose u. 2) Calculate du. 3) Substitute u. Arrange to have du in your integral also. (All xs and dxs must be replaced!) 4) Solve the new integral.
- Slides: 71