The subject of a formula Here is a

The subject of a formula Here is a formula you may know from physics: V = IR where V is voltage, I is current and R is resistance. V is called the subject of the formula. The subject of a formula always appears in front of the equals sign without any other numbers or operations. Sometimes it is useful to rearrange a formula so that one of the other variables is the subject of the formula. Suppose, for example, that we want to make I the subject of the formula V = IR.

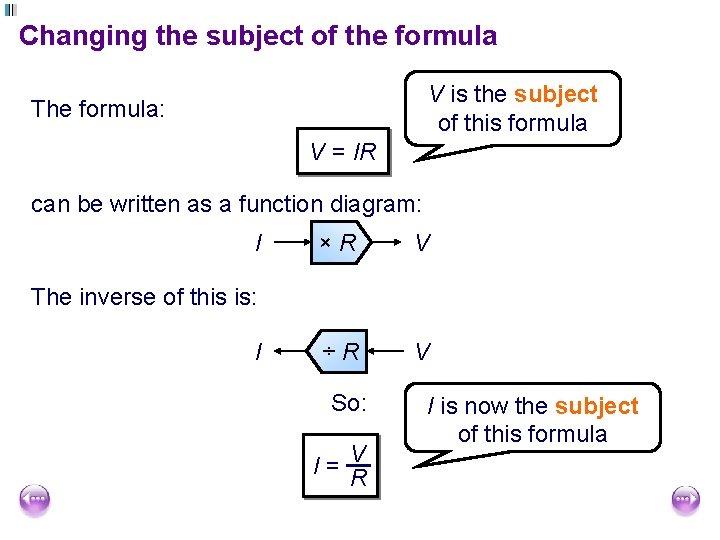
Changing the subject of the formula V is the subject of this formula The formula: V = IR can be written as a function diagram: I ×R V ÷R V The inverse of this is: I So: V I= R I is now the subject of this formula

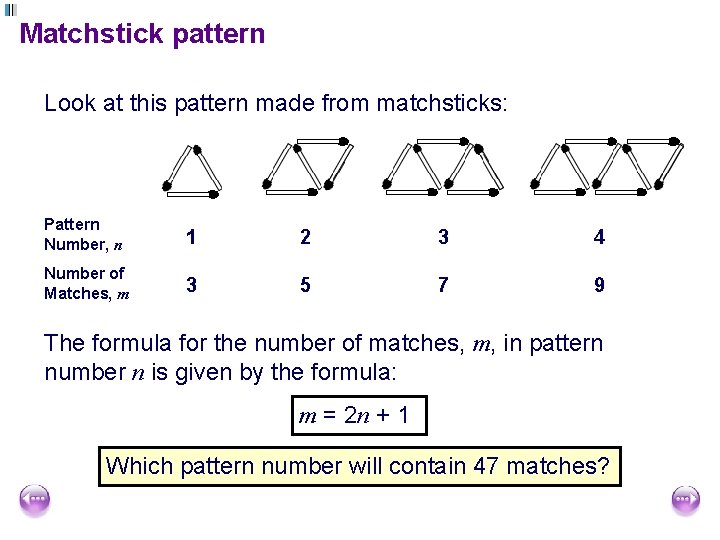
Matchstick pattern Look at this pattern made from matchsticks: Pattern Number, n 1 2 3 4 Number of Matches, m 3 5 7 9 The formula for the number of matches, m, in pattern number n is given by the formula: m = 2 n + 1 Which pattern number will contain 47 matches?

Changing the subject of the formula m is the subject of this formula The formula: m = 2 n + 1 can be written as a function diagram: n × 2 +1 m The inverse of this is: n ÷ 2 – 1 or m– 1 n= 2 m n is the subject of this formula

Changing the subject of the formula To find out which pattern will contain 47 matches, substitute 47 into the rearranged formula. m– 1 n= 2 47 – 1 n= 2 n= 46 2 n = 23 So, the 23 rd pattern will contain 47 matches.

Changing the subject of the formula We can also change the subject by performing the same operations on both sides of the equals sign. For example, to make C the subject of 9 C F= + 32 5 subtract 32: multiply by 5: divide by 9: 9 C F – 32 = 5 5(F – 32) = 9 C 5(F – 32) =C 9 5(F – 32) C= 9

Change the subject of the formula 1

Find the equivalent formulae

Formulae where the subject appears twice Sometimes the variable that we are making the subject of a formula appears twice. For example, S = 2 lw + 2 lh + 2 hw where S is the surface area of a cuboid, l is its length, w is its width and h is its height. Make w the subject of the formula. To do this we must collect all terms containing w on the same side of the equals sign. We can then isolate w by factorizing.

Formulae where the subject appears twice S = 2 lw + 2 lh + 2 hw Let’s start by swapping the left-hand side and the right-hand side so that the terms with w’s are on the left. 2 lw + 2 lh + 2 hw = S subtract 2 lh from both sides: 2 lw + 2 hw = S – 2 lh factorize: w(2 l + 2 h) = S – 2 lh divide by 2 l + 2 h: S – 2 lh w = 2 l + 2 h

Formulae involving fractions When a formula involves fractions we usually remove these by multiplying before changing the subject. For example, if two resistors with a resistance a and b ohms respectively, are arranged in parallel their total resistance R ohms can be found using the formula, 1 1 1 = + a b R aΩ Make R the subject of the formula bΩ

Formulae involving fractions 1 1 1 = + a b R multiply through by Rab: Rab Rab = + a b R simplify: ab = Rb + Ra factorize: ab = R(b + a) divide both sides by a + b: ab =R a+b ab R= a+b

Formulae involving powers and roots The length c of the hypotenuse of a right-angled triangle is given by c = √a 2 + b 2 where a and b are the lengths of the shorter sides. Make a the subject of the formula square both sides: subtract b 2 from both sides: square root both sides: c 2 = a 2 + b 2 c 2 – b 2 = a 2 √c 2 – b 2 = a a = √c 2 – b 2

Formulae involving powers and roots The time T needed for a pendulum to make a complete swing is T = 2π gl where l is the length of the pendulum and g is acceleration due to gravity. Make l the subject of the formula When the variable that we wish to make the subject appears under a square root sign, we should isolate it on one side of the equation and then square both sides.

Formulae involving powers and roots l g T = 2π divide both sides by 2π: T = 2π square both sides: T 2 l = g 4π2 multiply both sides by g: T 2 g = l 2 4π l g T 2 g l= 4π2

Change the subject of the formula 2